
2)夹角余弦 也可以直接利用两变量x与x的夹角余弦r来定义它们的相似性度量,有 x = (11) 它2 各种定义的相似度量均应具有以下两个性质: a)P≤1,对于一切j,k: b)「=,对于一切j,k。 越接近1,x,与x越相关或越相似。越接近零,x,与x的相似性越弱, 1.3.2变量聚类法 类似于样本集合聚类分析中最常用的最短距离法、最长距离法等,变量聚类法采用 了与系统聚类法相同的思路和过程。在变量聚类问题中,常用的有最大系数法、最小系 数法等。 1)最大系数法 在最大系数法中,定义两类变量的距离为 R(G.G2)=max) (12) 这时,R(G,G,)等于两类中最相似的两变量间的相似性度量值。 2)最小系数法 在最小系数法中,定义两类变量的距离为 (13) 这时,R(G,G)等于两类中相似性最小的两个变量间的相似性度量值。 例2服装标准制定中的变量聚类法。 在服装标准制定中,对某地成年女子的各部位尺寸进行了统计,通过14个部位的测 量资料,获得各因素之间的相关系数表 (见表2) 表5成年女子各部位相关系数 -453
-453- 2)夹角余弦 也可以直接利用两变量 j x 与 k x 的夹角余弦 jk r 来定义它们的相似性度量,有 2 1 1 2 1 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ∑ ∑ ∑ = = = n i ik n i ij n i ij ik jk x x x x r (11) 各种定义的相似度量均应具有以下两个性质: a) rjk ≤1,对于一切 j, k ; b) jk kj r = r ,对于一切 j, k 。 jk r 越接近1, j x 与 k x 越相关或越相似。 jk r 越接近零, j x 与 k x 的相似性越弱。 1.3.2 变量聚类法 类似于样本集合聚类分析中最常用的最短距离法、最长距离法等,变量聚类法采用 了与系统聚类法相同的思路和过程。在变量聚类问题中,常用的有最大系数法、最小系 数法等。 1)最大系数法 在最大系数法中,定义两类变量的距离为 ( , ) max{ } 2 1 1 2 jk x G x G R G G r k j ∈ ∈ = , (12) 这时, ( , ) R G1 G2 等于两类中最相似的两变量间的相似性度量值。 2)最小系数法 在最小系数法中,定义两类变量的距离为 ( , ) min{ } 2 1 1 2 jk x G x G R G G r k j ∈ ∈ = , (13) 这时, ( , ) R G1 G2 等于两类中相似性最小的两个变量间的相似性度量值。 例2 服装标准制定中的变量聚类法。 在服装标准制定中,对某地成年女子的各部位尺寸进行了统计,通过14个部位的测 量资料,获得各因素之间的相关系数表(见表2)。 表5 成年女子各部位相关系数 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x
0.36】 40.2120.231 540.28Q.1940591 50.360.3240.4760.4s1 60.220.220.480.470.421 与0.215Q.26猫0.510.4780.550.631 40.4180.3450.4520.4040.4310.320.261 50.486036i0360.3570.490.2g0.28m70.821 。0.6480.6e0.2160.030.40283a2830.5270.5471 t0.6890.610.2430.3130.430.300.2940.520.5809571 0.4860.6360.1740.2480.3750.2960.25040g0.4170.57a8521 0.130.1530.7320.4770.390.392a.44602660.210.0540.090.05 340.3760.2520.6760.5810.410.4470.40.4240.320.330.376Q.3210.6271 其中x一上体长,3一手臂长,x一胸围,x一颈围,x一总肩围,x6一总胸宽,x 后背宽,x一前腰节高,x)一后腰节高,x。一总体长,x1一身高,x2一下体长,x, 腰围,x4-臀围。用最大系数法对这14个变量进行系统聚类,分类结果如图3。 图3成年女子14个部位指标的聚类图 454
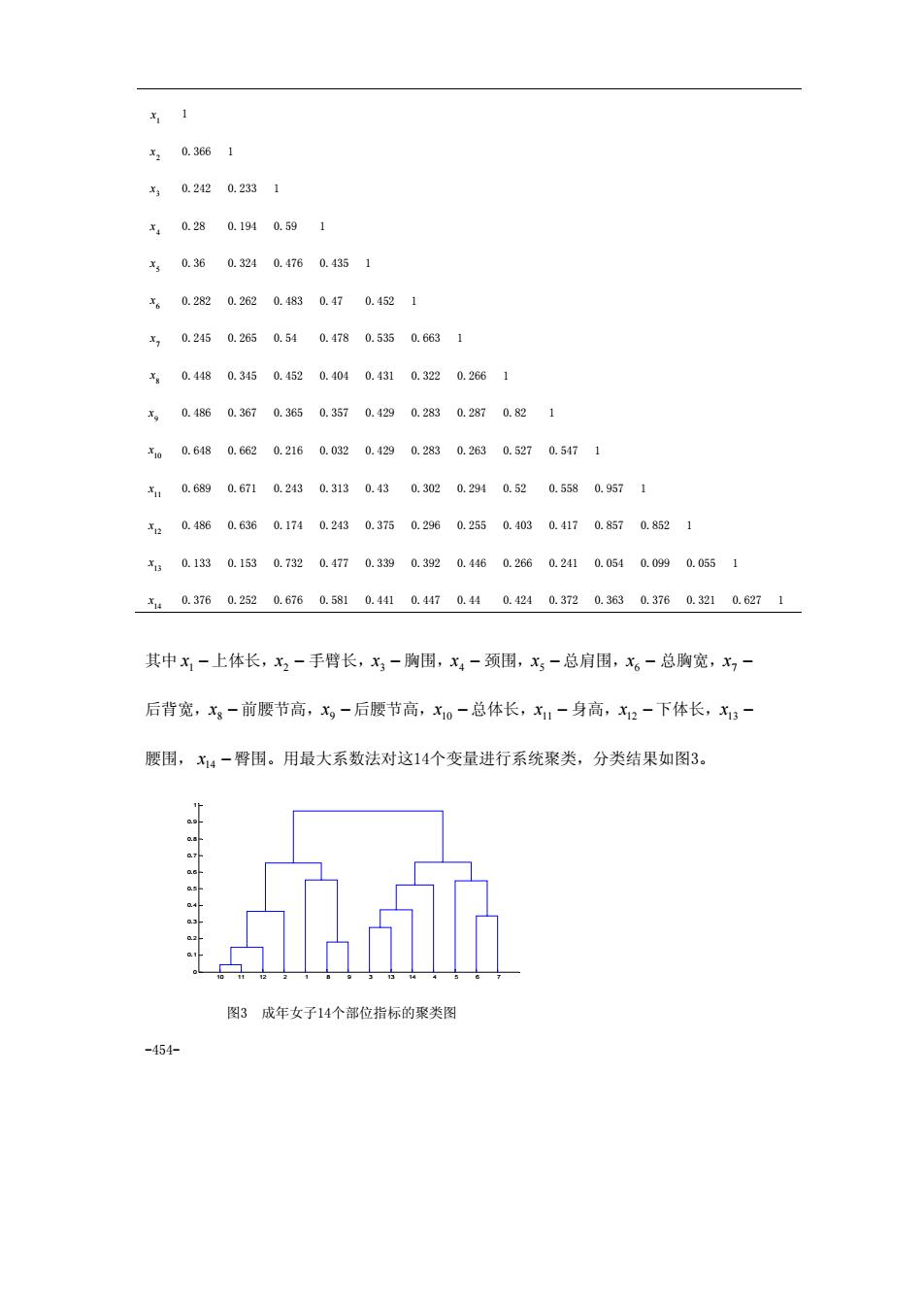
-454- 1 x 1 2 x 0.366 1 3 x 0.242 0.233 1 4 x 0.28 0.194 0.59 1 5 x 0.36 0.324 0.476 0.435 1 6 x 0.282 0.262 0.483 0.47 0.452 1 7 x 0.245 0.265 0.54 0.478 0.535 0.663 1 8 x 0.448 0.345 0.452 0.404 0.431 0.322 0.266 1 9 x 0.486 0.367 0.365 0.357 0.429 0.283 0.287 0.82 1 10 x 0.648 0.662 0.216 0.032 0.429 0.283 0.263 0.527 0.547 1 11 x 0.689 0.671 0.243 0.313 0.43 0.302 0.294 0.52 0.558 0.957 1 12 x 0.486 0.636 0.174 0.243 0.375 0.296 0.255 0.403 0.417 0.857 0.852 1 13 x 0.133 0.153 0.732 0.477 0.339 0.392 0.446 0.266 0.241 0.054 0.099 0.055 1 14 x 0.376 0.252 0.676 0.581 0.441 0.447 0.44 0.424 0.372 0.363 0.376 0.321 0.627 1 其中 x1 − 上体长,x2 − 手臂长,x3 − 胸围,x4 − 颈围,x5 − 总肩围,x6 − 总胸宽,x7 − 后背宽,x8 − 前腰节高,x9 −后腰节高,x10 −总体长,x11 − 身高,x12 −下体长,x13 − 腰围, x14 −臀围。用最大系数法对这14个变量进行系统聚类,分类结果如图3。 10 11 12 2 1 8 9 3 13 14 4 5 6 7 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 图3 成年女子14个部位指标的聚类图

计算的ATLAB程序如下: %把下三角相关系数矩阵粘贴到纯文本文件ch.txt中 a(i,i)=0: end b=a(:)b=nonzeros(b):b=b':b=1-b; z=linkage(b,'complete'); =cluster(,2) dendrogram(z) indl=find(y==2):indl=ind1' ind2=find(y==1):ind2=ind2' 可以看出,人体的变量大体可以分为两类:一类反映人高、矮的变量,如上体长, 手臂长,前腰节高,后腰节高,总体长,身高,下体长:另一类是反映人体胖瘦的变量 如胸用,颈,总肩围,总胸宽,后背宽,腰用,臀围 §2聚类分析案例一我国各地区普通高等教有发展状况分析 聚类分析又称群分析,是对多个样本(或指标)进行定量分类的一种多元统计分析 方法。对样本进行分类称为Q型聚类分析,对指标进行分类称为R型聚类分析。本案例 运用Q型和R型聚类分析方 对我国各地区普通高等教有的发展状况进行分析 1.采例研究背景 近年来,我国普通高等教有得到了迅速发展,为国家培养了大批人才。但由于我国 各地区经济发展水平不均衡,加之高等院校原有布局使各地区高等教有发展的起点不一 致,因而名地风普通高等教有的发展水平存在一定的差异。不同的地风具有不同的特 点。对我国各地区普通高等教有的发展状况进行聚类分析,明确各类地区普通高等教有 发展状况的差 与特点,有利于管理和决策部门 从宏规 上把握我国普通高等教有的整 发展现状,分类制定相关政策,更好的指导和规划我国高教事业的整体健康发展。 2.案例研究过程 (1)建立综合评价指标体系 高等教育是依赖高等院校进行的,高等教育的发展状况主要体现在高等院校的 关方面。连循可比性原则,从高等教有的五个方面选取十项评价指标,具体如图4。 (2)数据资料 指标的原始数据取自《中国统计年鉴,1995》和《中国教有统计年鉴,1995》除以 各地区相应的人口数得到十项指标值见表6。其中:x为每百万人口高等院校数::为 每十万人口高等院校毕业生数:x为每十万人口高等院校招生数:x,为每十万人口高 等院校在校生数:x,为每十万人口高等院校教职工数:x。为每十万人口高等院校专职 -455
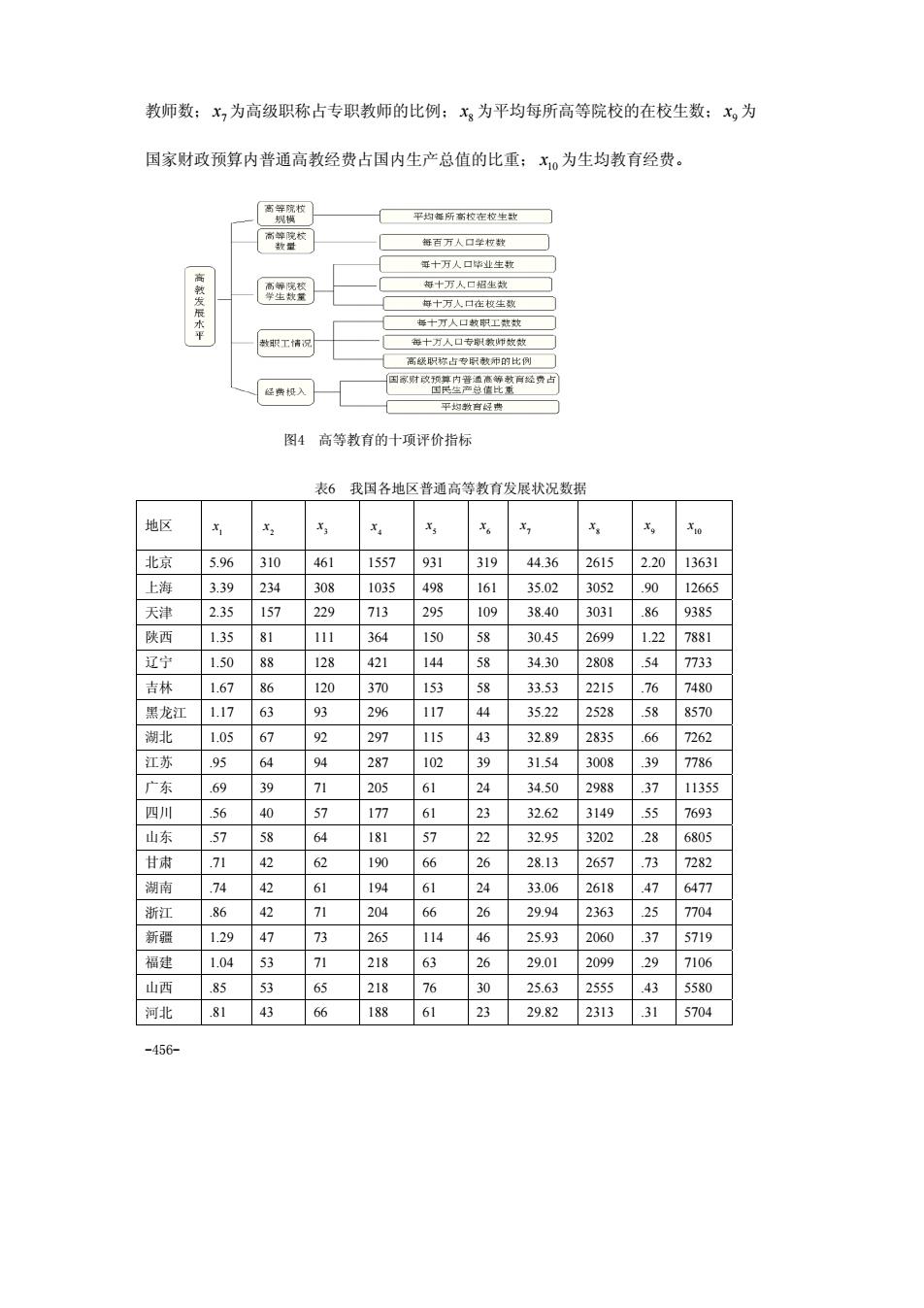
-455- 计算的MATLAB程序如下: %把下三角相关系数矩阵粘贴到纯文本文件ch.txt中 a=textread('ch.txt'); for i=1:14 a(i,i)=0; end b=a(:);b=nonzeros(b);b=b';b=1-b; z=linkage(b,'complete'); y=cluster(z,2) dendrogram(z) ind1=find(y==2);ind1=ind1' ind2=find(y==1);ind2=ind2' 可以看出,人体的变量大体可以分为两类:一类反映人高、矮的变量,如上体长, 手臂长,前腰节高,后腰节高,总体长,身高,下体长;另一类是反映人体胖瘦的变量, 如胸围,颈围,总肩围,总胸宽,后背宽,腰围,臀围。 §2 聚类分析案例—我国各地区普通高等教育发展状况分析 聚类分析又称群分析,是对多个样本(或指标)进行定量分类的一种多元统计分析 方法。对样本进行分类称为Q型聚类分析,对指标进行分类称为R型聚类分析。本案例 运用Q型和R型聚类分析方法对我国各地区普通高等教育的发展状况进行分析。 1.案例研究背景 近年来,我国普通高等教育得到了迅速发展,为国家培养了大批人才。但由于我国 各地区经济发展水平不均衡,加之高等院校原有布局使各地区高等教育发展的起点不一 致,因而各地区普通高等教育的发展水平存在一定的差异, 不同的地区具有不同的特 点。对我国各地区普通高等教育的发展状况进行聚类分析,明确各类地区普通高等教育 发展状况的差异与特点,有利于管理和决策部门从宏观上把握我国普通高等教育的整体 发展现状,分类制定相关政策,更好的指导和规划我国高教事业的整体健康发展。 2.案例研究过程 (1)建立综合评价指标体系 高等教育是依赖高等院校进行的,高等教育的发展状况主要体现在高等院校的相 关方面。遵循可比性原则,从高等教育的五个方面选取十项评价指标,具体如图4。 (2)数据资料 指标的原始数据取自《中国统计年鉴,1995》和《中国教育统计年鉴,1995》除以 各地区相应的人口数得到十项指标值见表 6。其中: 1 x 为每百万人口高等院校数; 2 x 为 每十万人口高等院校毕业生数; 3 x 为每十万人口高等院校招生数; 4 x 为每十万人口高 等院校在校生数; 5 x 为每十万人口高等院校教职工数; 6 x 为每十万人口高等院校专职
教师数:X,为高级职称占专职教师的比例:x。为平均每所高等院校的在校生数:X。为 国家财政预算内普通高教经费占国内生产总值的比重:x。为生均教有经费。 平妈篷所高校宿拉牛计 每人口学板 高教发版 生 十万人口职工数 果工情况 图4 高等教有的十项评价指 表6我国各地区普通高等教有发展状况数据 地区 北京 310 1557 93 44.3 363 上海 3.39 234 308 1035 498 161 35.02 3052 90 12665 天津 2.35 157 229 713 295 10938.40 3031 86 9385 味6135 81 111364 150 58 30.45 2699 122 78 1.5 42 34.30 2808 73 吉林 1.67 86 120 370 153 33.53 2215 .76 7480 里龙江1.1763 93 296 117 44 35.222528 58 8570 湖北 61 297 115 43 32.89 2835 T262 95 287 31.5 3008 39 7786 东 69 39 71 205 61 24 34.50 2988 .37 11355 四 56 40 57 177 61 23 3262 314055 7693 山东 57 58 64 181 32.95 3202 6805 甘 .71 62 190 66 9/ 28.13 2657 .73 1282 湖南 .74 42 61 194 61 24 33.06 2618 .47 6477 浙订 86 42 71 204 66 26 29.94 2363 25 7704 新强 129 41 73 265 114 46 25.93 2060 17 5719 1.0 71 218 63 29.01 2099 29 7106 山西 85 53 65 218 76 30 25.63 2555 .43 5580 河北 81 43 66 188 61 23 29.82 2313315704 -456
-456- 教师数; 7 x 为高级职称占专职教师的比例; 8 x 为平均每所高等院校的在校生数; 9 x 为 国家财政预算内普通高教经费占国内生产总值的比重; 10 x 为生均教育经费。 图4 高等教育的十项评价指标 表6 我国各地区普通高等教育发展状况数据 地区 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 北京 5.96 310 461 1557 931 319 44.36 2615 2.20 13631 上海 3.39 234 308 1035 498 161 35.02 3052 .90 12665 天津 2.35 157 229 713 295 109 38.40 3031 .86 9385 陕西 1.35 81 111 364 150 58 30.45 2699 1.22 7881 辽宁 1.50 88 128 421 144 58 34.30 2808 .54 7733 吉林 1.67 86 120 370 153 58 33.53 2215 .76 7480 黑龙江 1.17 63 93 296 117 44 35.22 2528 .58 8570 湖北 1.05 67 92 297 115 43 32.89 2835 .66 7262 江苏 .95 64 94 287 102 39 31.54 3008 .39 7786 广东 .69 39 71 205 61 24 34.50 2988 .37 11355 四川 .56 40 57 177 61 23 32.62 3149 .55 7693 山东 .57 58 64 181 57 22 32.95 3202 .28 6805 甘肃 .71 42 62 190 66 26 28.13 2657 .73 7282 湖南 .74 42 61 194 61 24 33.06 2618 .47 6477 浙江 .86 42 71 204 66 26 29.94 2363 .25 7704 新疆 1.29 47 73 265 114 46 25.93 2060 .37 5719 福建 1.04 53 71 218 63 26 29.01 2099 .29 7106 山西 .85 53 65 218 76 30 25.63 2555 .43 5580 河北 .81 43 66 188 61 23 29.82 2313 .31 5704
安潜 59 35 47 146 46 20 3283 2488 33 5628 云南66 36 40 130 44192855 1974 489106 江西 4 6 23288 2515 34 4081 海南 .70 33 51 165 47 1827.34 2344 28 7928 内蒙古 84 43 48 171 65 2927.65 2032 32 5581 西藏1.6926 45 13775331210810 100 14199 河 53 32 17284 234 571 西 .60 28 43 129 39 1731.93 2146 245139 宁夏 1.39 48 62 208 77 3422.70 1500 42 5377 贵州642332 03371638131460 34415 青海 1.48 38 46 151 3017.87 1024 38 (3)R型聚类分析 定性考察反映高等教有发展状况.的五个方面十项评价指标,可以看出,某些指标之 间可能存在较强的相关性。比如每十万人口高等院校毕业生数、每十万人口高等院校招 生数与每十万人口高等院校在校生数之间可能存在较强的相关性 每十万人口高等 校教职工数和每十万人口高等院校专职教师数之间可能存在较强的相关性。为了验证这 种想法,运用MATLAB软件计算十个指标之间的相关系数,相关系数矩阵如表6所示。 表6相关系数矩阵 x X. x。 1.0000094340.9528 0.95910.97460.97980.40650.06630.86800.6609 0.9434 1.0000 0.9946 0.994d 0.9743 0.970 Q6136 0.3500 0.8039 0.599 0.95280.9946 1.0000 0.9987 0.9831 0.9807 0.6261 034450.8231 0.6171 0.9591 0.9946 0.998 000 0.9878 0.9856 0.6096 0.3256 0.8276 0.6124 0.9746 0.97430.983 0.9878 1.0000 0.9986 0.5599 02411 0.8590 0.6174 0.97980.9702 0.9807 0.9856 0.9986 1.0000 0.5500 02222 0.8691 0.6164 0.4065 0.6136 0.626 0.6096 0.5599 05500 1.0000 0.7789 0.3655 0.1510 0.06630.35000.344 0.325602411 02222 0.7789 1.00000.1122 0.0482 0.86800.80390.8231 8276 0.8590 0.8691 0.3655 0.1122 1.0000 0.6833 0.66090.59980.6171 0.61240.61740.6164 0.1510 0.04820.6833 1.0000 可以看出某些指标之间确实存在很强的相关性,因此可以考虑从这些指标中选取 457
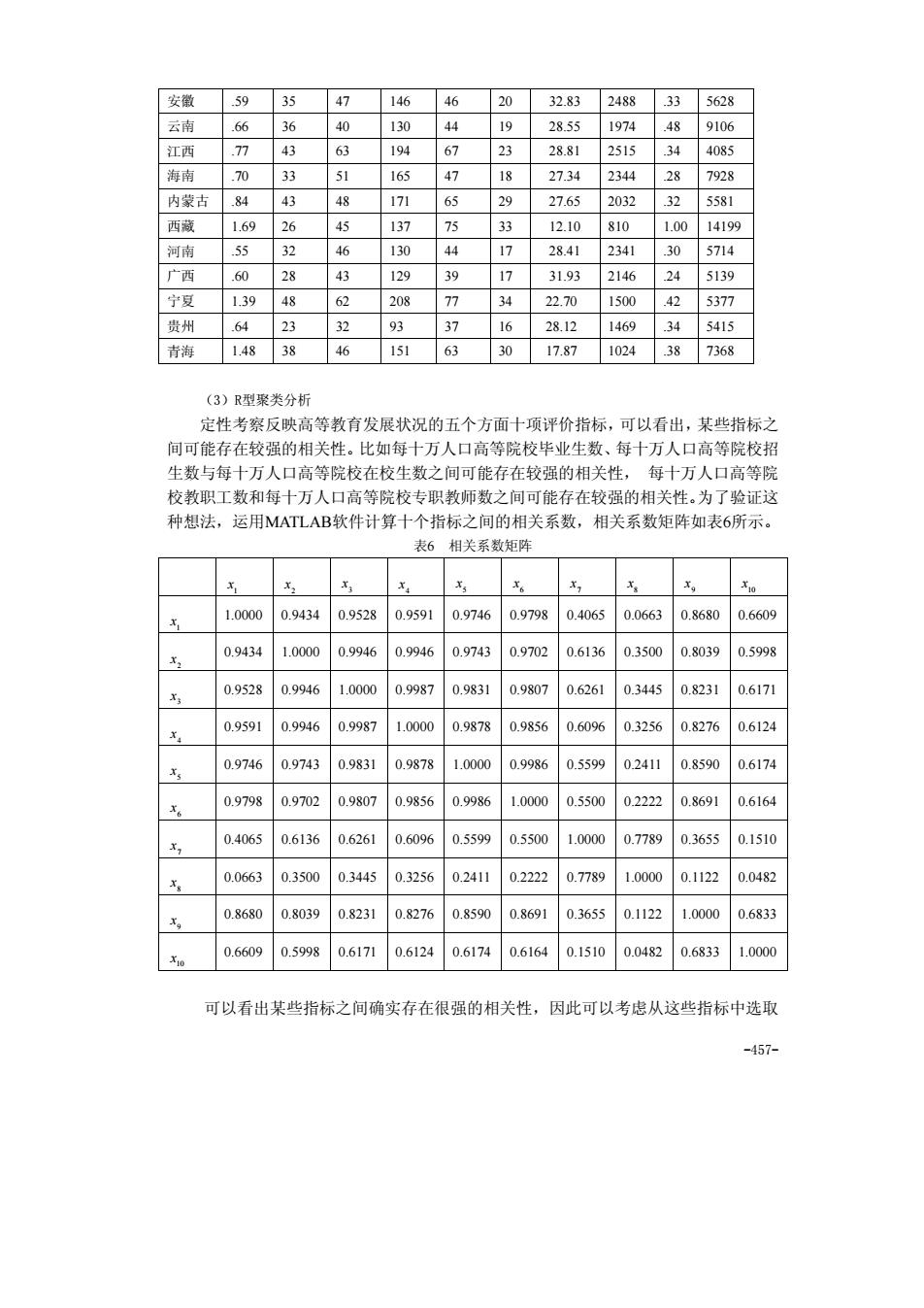
-457- 安徽 .59 35 47 146 46 20 32.83 2488 .33 5628 云南 .66 36 40 130 44 19 28.55 1974 .48 9106 江西 .77 43 63 194 67 23 28.81 2515 .34 4085 海南 .70 33 51 165 47 18 27.34 2344 .28 7928 内蒙古 .84 43 48 171 65 29 27.65 2032 .32 5581 西藏 1.69 26 45 137 75 33 12.10 810 1.00 14199 河南 .55 32 46 130 44 17 28.41 2341 .30 5714 广西 .60 28 43 129 39 17 31.93 2146 .24 5139 宁夏 1.39 48 62 208 77 34 22.70 1500 .42 5377 贵州 .64 23 32 93 37 16 28.12 1469 .34 5415 青海 1.48 38 46 151 63 30 17.87 1024 .38 7368 (3)R型聚类分析 定性考察反映高等教育发展状况的五个方面十项评价指标,可以看出,某些指标之 间可能存在较强的相关性。比如每十万人口高等院校毕业生数、每十万人口高等院校招 生数与每十万人口高等院校在校生数之间可能存在较强的相关性, 每十万人口高等院 校教职工数和每十万人口高等院校专职教师数之间可能存在较强的相关性。为了验证这 种想法,运用MATLAB软件计算十个指标之间的相关系数,相关系数矩阵如表6所示。 表6 相关系数矩阵 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 1 x 1.0000 0.9434 0.9528 0.9591 0.9746 0.9798 0.4065 0.0663 0.8680 0.6609 2 x 0.9434 1.0000 0.9946 0.9946 0.9743 0.9702 0.6136 0.3500 0.8039 0.5998 3 x 0.9528 0.9946 1.0000 0.9987 0.9831 0.9807 0.6261 0.3445 0.8231 0.6171 4 x 0.9591 0.9946 0.9987 1.0000 0.9878 0.9856 0.6096 0.3256 0.8276 0.6124 5 x 0.9746 0.9743 0.9831 0.9878 1.0000 0.9986 0.5599 0.2411 0.8590 0.6174 6 x 0.9798 0.9702 0.9807 0.9856 0.9986 1.0000 0.5500 0.2222 0.8691 0.6164 7 x 0.4065 0.6136 0.6261 0.6096 0.5599 0.5500 1.0000 0.7789 0.3655 0.1510 8 x 0.0663 0.3500 0.3445 0.3256 0.2411 0.2222 0.7789 1.0000 0.1122 0.0482 9 x 0.8680 0.8039 0.8231 0.8276 0.8590 0.8691 0.3655 0.1122 1.0000 0.6833 10 x 0.6609 0.5998 0.6171 0.6124 0.6174 0.6164 0.1510 0.0482 0.6833 1.0000 可以看出某些指标之间确实存在很强的相关性,因此可以考虑从这些指标中选取