
四.名词定义 状态:表示动态系统的一组最少变量(被称为状 态变量),只要知道t=t,时这组变量和t≥t,时的 输入,那么就能完全确定系统在任何时间t≥t,的行 为。 状态变量:能够表示系统状态的那些变量成为状态 变量。例如上例中的i,(t),yc(t)
四.名词定义 状态:表示动态系统的一组最少变量(被称为状 态变量),只要知道 时这组变量和 时的 输入,那么就能完全确定系统在任何时间 的行 为。 0 t = t 0 t t 0 t t 状态变量:能够表示系统状态的那些变量成为状态 变量。例如上例中的 i L (t), vC (t)

状态矢量:能够完全描述一个系统行为的k个状 态变量,可以看作矢量的条个分量的坐标。 称 为状态矢量。 状态空间:状态矢量2(t)所在的空间。 状态轨迹:在状态空间中状态矢量端点随时间变化 而描出的路径称为状态轨迹
状态矢量:能够完全描述一个系统行为的k个状 态变量,可以看作矢量 的各个分量的坐标。 称 为 状态矢量 (t) 。 (t) 状态轨迹:在状态空间中状态矢量端点随时间变化 而描出的路径称为状态轨迹。 状态空间:状态矢量 (t)所在的空间

§12.2 连续时间系统状态方程的建立 状态变量 用来描述网络中一状态随时间变化的变 量,称之为状态变量。 状态方程 描述了系统状态变量的一阶导数与状态 变量和激励关系的一阶微分方程,称为状态 方程。 GC款G0o水恕G包卷尚尽@句入9道
§12.2 连续时间系统状态方程的建立 状态变量 用来描述网络中一状态随时间变化的变 量,称之为状态变量。 状态方程 描述了系统状态变量的一阶导数与状态 变量和激励关系的一阶微分方程,称为状态 方程
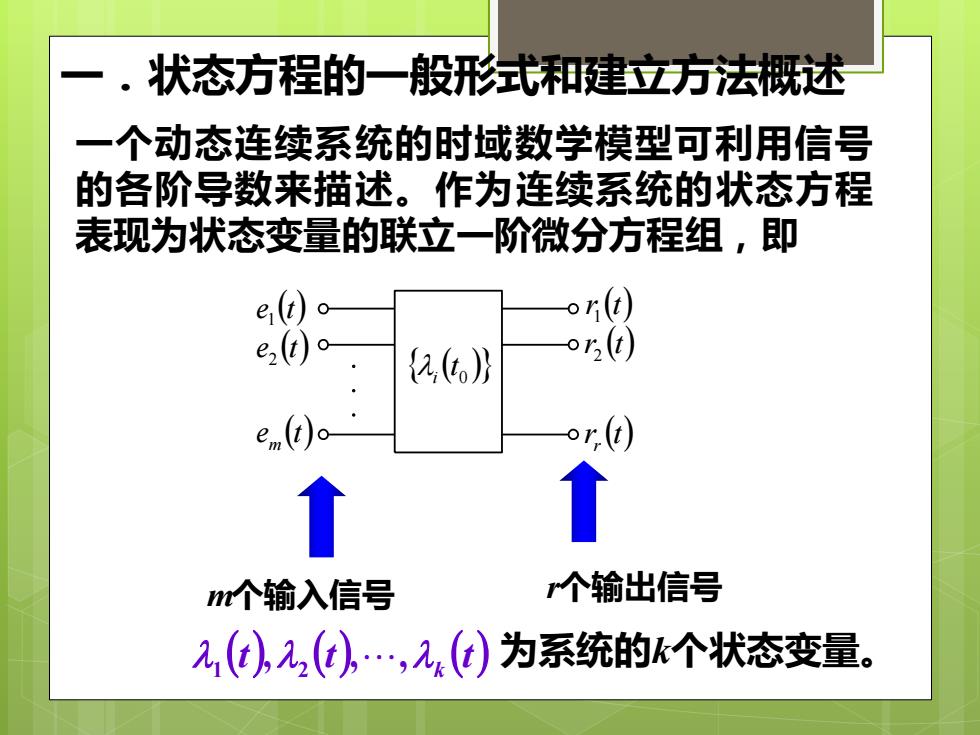
状态方程的一般形式和建立方法概述 一个动态连续系统的时域数学模型可利用信号 的各阶导数来描述。作为连续系统的状态方程 表现为状态变量的联立一阶微分方程组,即 e(1)o or(t) e20)o {2,6} or,(t) e(t)o o.) nm个输入信号 个输出信号 2,(t),(t),2(d)为系统的k个状态变量
一.状态方程的一般形式和建立方法概述 e (t) 1 e (t) 2 e (t) m . . . r (t) 1 r (t) 2 r (t) r i (t 0 ) 一个动态连续系统的时域数学模型可利用信号 的各阶导数来描述。作为连续系统的状态方程 表现为状态变量的联立一阶微分方程组,即 (t) (t) (t) k , , , 1 2 为系统的k个状态变量。 m个输入信号 r个输出信号

状态方程 i2,),.,(0hed),e,.,en),] dt 品2-kA1Aae6-a.e d)=f[2,),(),.,e,e2),.,en),] 输出方程 r0)=h[d,d).,()e,),e2,.,en),] 5)=h[,(),2).,(te,e2t,.,enm(d,] yd)=h,[,d,2,.,ted,e2t,.,em(,t]
状态方程 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = = r t h t t t e t e t e t t r t h t t t e t e t e t t r t h t t t e t e t e t t r r k m k m k m , , , ; , , , , , , , ; , , , , , , , ; , , , , 1 2 1 2 2 2 1 2 1 2 1 1 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = = t f t t t e t e t e t t t t f t t t e t e t e t t t t f t t t e t e t e t t t k k k m k m k m , , , ; , , , , d d , , , ; , , , , d d , , , ; , , , , d d 1 2 1 2 2 2 1 2 1 2 1 1 1 2 1 2 输出方程