
S1.3能量守恒一热力学第一定律 如上所述,U为一状态性质,所以△U只取决于系统的始态和终态,而与变化 的途径无关。热力学能的绝对值现在还无法测量,然而对热力学来说,重要的 不是热力学能的绝对值而是热力学能的变化值,因为这是可以用实验测量的 物理量。 如果系统的状态变化无限小,则热力学能变化可表示为U,由于U是状态 性质,所以U在数学上是金微分。前面讲到,对纯物质单相帝闭系统来说,通 常只要确定两个状态性质,系统的状态就确定了。当然热力学能U亦就随之而 定了。所以,可以将系统的热力学能看做是任意两个状态性质的函数。例如,将 V看做是温度T和体积V的函数,U=(T,)。那么根据多元函数的微分,U的 全微分可写为 d0=(9r+,4v (1.2) 2.功和热的概念 当系统的状态发生变化并引起系统的能量发生变化时,这种能量的变化必 须依獭于系统和环境之间的能量传递来实现。系统与环境之间的能量传递形式 可区分为两种方式,一种叫做“热”,另一种叫做“功”。由于系统与环境之间的 温度差而造成的能量传递称为“热”:除了热以外,在系统与环境之间其他形式 的能县传递统称为“功”。热和功总是与系统所进行的具体过程相联系着的,没 有过程就没有热和功,因此热和功不是状态性质,它们与途径有关。如果说系统 的某一状态有多少热或有多少功,这是毫无意义的。因为当传递过程一结束,功 和热都转化为系统热力学能的改变。这就是热和功与热力学能在概念上的主要 区别。 在热力学中,热用符号Q米表示,根据UPAC(国际理论与应用化学联合 会)的建议系统吸热为正值,而系统放热为负值。功用符号甲来表示,以系统对 环境做功为负值,而以环境对系统做功为正值。 3.热力学第一定律的数学表达式 当一系统的状态发生某一任意变化时,假设系统吸收的热量为Q,同时得到 的功为W,那么根据热力学第一定律,应当有下列公式 △U=Q+W (1.3) 这就是热力学第一定律的数学表达式。此式表明,一个封闭系统其热力学能的 增加等于系统从环境所吸收的热量与环境对系统所做功之和。 如果系统状态只发生一无限小量的变化,则(1.3)式可写为 d0=6Q+6W (1.4)引 因为功和热都不是状态性质,故用8Q和8W而不用dQ和W以表示它们不是 全微分。 11
第一章热力学第一定律 匀有电护丝手大水中强宗接上电女电流段时阿如乘 按列种情况作为系统试Q旷为正为负还是岁零? 2以电炉丝和水为 所示心将隔板去以后空气为系统时4心 亦有气还过年力较左方小 将隔板去以后以所有 题3·1少如果 统从环境接受了“160J 学能增加了200J试问系统将 吸收或是放出少热?〔)只系统在膨张过程 可1050 27110的热试同系统的热力学能变化为若 习题4如图所茶,系统状态工沿途径1 变到状态之时,从环境吸收了1401的热,同时对环境 了170J的功试向门)当系统沿途径 时,系统对环境做4的功这 2如来系统沿径由状态2回到状态:环境对 微了9红的功则系统将吸收或是放出多热 [答案1240J29微热2765 习题 礼堂销有950在 ,每人 热量如果以礼丝中的空气和椅子系统则在于 作2 心,试求算此过程客电池将吸收还是出多少热? 12

S1.4体积功 §1.4体积功 1.体积功 因系统体积变化而引起的系统与环境间交换的功称为体积功。休积功在热 力学中有者特殊的意义。设一圆筒内盛有气体,圆简 的藏面积为A,简上有一无质量、无摩擦力的理想活 塞,活塞的外压力为P外,则圆简活塞上所受到的外力 为P外·A(见图1.3)。当气体膨胀,将活塞向外推了 l的距离时,所作之功为 6W=-fdl=“pAdl=-P外dV (1.5) dV是膨胀时气体体积的变化,所以体积功可以用 -P外dV米表示,P外是活塞上的外压力,负号是因为 A 规定系统对环境做功为负。 图1.3体积功 关于体积功有两点要注意。其一,不论系统是膨 张还是压缩,体积功都用-P外dV米计算;其二,只有PmdV这个量才是体积功 pV,pdV或V阳p都不是体积功 前面讲到,功不是状态性质,而是与途径有关的。现通过计算一气体具有 相同的始态、终态而途径不同的几种定温过程的影胀功,来表明功是与途径有 关的量。为了使气体在定温下膨张,可将圆筒放在一恒温糟中,让气体的体积 从V,膨胀到V2。当定温膨胀的方式不同时,系统所做的功的数值也将不同。 例如: (1)气体向真空膨胀(图1.4)。此时施加在活塞上的外压为零,即P=0, 所以在膨胀过程中系统没有对环境做功,即 W=0 真空P0 25℃, 2×10Pa 5dm 25℃,10a 图1.4气体向真空影胀 13
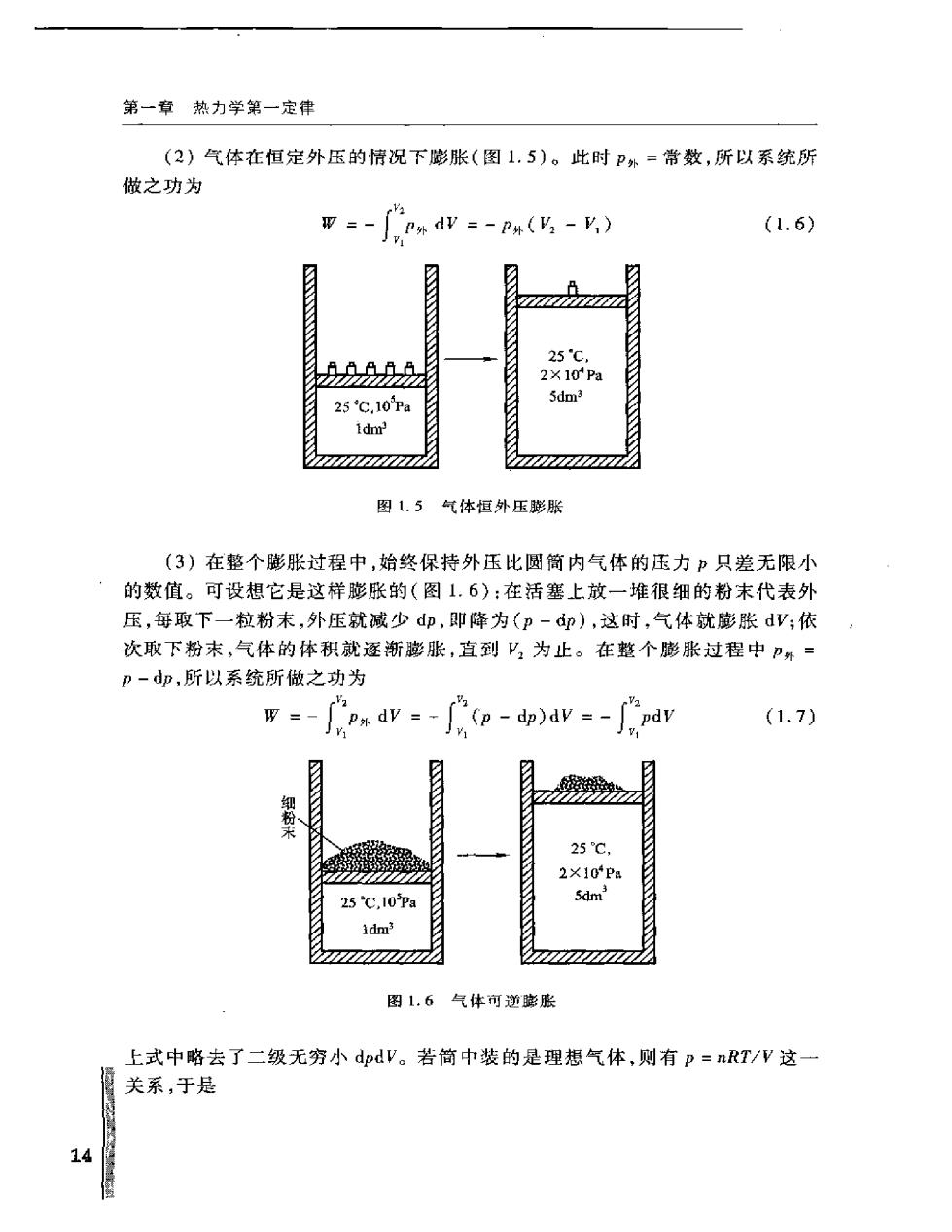
第一章热力学第一定律 (2)气体在恒定外压的情况下膨胀(图1.5)。此时P外=常数,所以系统所 做之功为 -dv-Ps(V-V.) (1.6) 25℃.10a 1dm 图1.5气体恒外压膨胀 (3)在整个膨胀过程中,始终保持外压比圆简内气体的压力p只差无限小 的数值。可设想它是这样膨胀的(图1.6):在活塞上放一堆很细的粉末代表外 压,每取下一粒粉末,外压就减少d即,即降为(p-dp),这时,气体就膨张dV;依 次取下粉末,气体的体积就逐渐膨胀,直到'2为止。在整个膨胀过程中= p-dp,所以系统所做之功为 ps dv =-fcp-dp)dv =-pdv (1.7) 25C. 25℃,10pa idm 图.6气体可逆膨胀 上式中略去了二级无穷小dpdV。若简中装的是理想气体,则有p=nRT/V这 关系,于是

S1.4体积功 wagFav n =-nRT In色 (1.8) 以上式中均以右下标“1”表示始态,“2”表示终态。很显然上述三种情况虽 始态、终态相同,但功的数值却不相同,证明了功是与途径有关的量。 2,可逆过程与不可逆过程 在上述的三种膨胀方式中,第三种膨胀方式是热力学中一种极为重要的过 程。由于这种膨胀方式需要无限多次手续,所以是无限缓慢的。 如果将取下的松末一粒粒重新加到活塞上,则在此压缩过程中,外压始终只 比圆筒内气体的压力大dp,一直回复到Y,为止。在此压缩过程中所做之功为 w=-f"on dv =-f"(p+do)dv =-fpdy (1.9) 比较式(1.7)和式(1.9)可看出,这种无限缓慢的膨胀过程所做之功和无限缓慢 的压缩过程所做之功,大小相等而符号相反。这就是说,当系统回复到原来状态 时,在环境中设有功的得失;由于系统回到原状,总计△U=0,根据△U=Q+W 所以在环境中亦无热的得失;亦即当系统回复到原状时,环境亦回复到原状。某 过程进行之后系统恢复原状的同时,环境也能恢复原状而未留下任何永久性的 变化,则该过程称为“热力学可逆过程”。上述第三种临胀方式就属于可逆 过程。 如果系统发生了某一过程之后,在使系统恢复原状的同时,环境中必定会留 下某种永久性变化,即环境没有完全复原,则此过程称为“热力学不可逆过程”。 如上述第一种和第二种膨胀方式即属于此。例如,在第二种膨胀方式发生后,欲 使气体从'压缩回到V,在压缩过程中,环境所消耗的功必然大于原来在膨胀 过程中环境所得到的功,因为压缩时的P外一定大于膨胀时的P外。因此,即使系 统恢复到原状,环境中将有功的损失,即有永久性变化,所以第二种膨胀方式是 不可逆过程。 在上述三种定温膨张过程中,始态和终态均相同,因此体积的变化亦都相 同,△V=V2-V:。因此在这些不同的膨胀过程中,功的大小取决于外压P饼的数 值,P越大,则系统所做之功越大。在可逆膨胀过程中,由于P外始终只比P差 无限小的数值,亦即系统在膨胀时对抗了最大的外玉,所以在定温的情况下,系 统在可逆过程中所做的功为最大功(绝对值)。同理,在压缩过程中,P外越小, 则环境所消耗的功越小:而在可逆压缩过程中,由于P始终只比p大无限小的 数值,亦即压缩时环境只使用了最小的外玉,所以在定温的情况下,环境在可逆 过程中所消耗的功为最小功