
16食品工程原理 时水的流量,已知管内径为12mm。 解:用柏努利方程进行近似计算,取水箱液面 为第一截面,龙头出口为第二截面。由于第一截面 面积远大于龙头出口,故其速度“1可以忽略, 爱=A2+二 又因两截面均与大气接触,故截面上流体压力 相等,均为大气压,从而上式简化为: 例题1-2附图 u2=√-2g△2=√2×9.81×10=14(m/s) 水的流量为: Q=d2u2=0.785×0.0122×14=1.58×10-3(m3/s) 3.4不可压缩实际流体的稳定流动 在流体输送中,分子之间的摩擦力将不可避免地造成机械能损失。根据能量 守恒原理,损失的机械能转变为分子的内能。在流体流动计算中,我们称这部分 内能为摩擦损失或水头损失。在体系与外界无热量交换情况下,不可压缩实际流 体的稳定流动能量平衡方程为: 购+g+艺+w=函+2+竖+(ea61) (1-31a) 0 乙+0+是+H=2a+0+爱+。0 g (1-31b) 或 肠+日+受+w=肠+g+兰+公: (1-31c) 名+极+器+H-石+品+爱+公 (1-31d) 式中∑:和∑:分别称为单位质量和单位重量流体流动过程中的摩擦损失或

第1章流体力学基础17 水头损失,关于该项的求解将是我们下面重点讨论的内容;H为输送设备的压 头或扬程。 管中流动 按流体与固体的接触情况来分,流体运动主要有下列四种形式:一是流体在 固体内部的管中流动和缝隙流动;二是流体在固体外部的绕流;三是流体在固体 一侧的表面流动;四是流体与固体不接触的孔口出流和射流。在食品工程中,以 第一种流动形式最普遍,如空气和蒸汽在管道中的流动,水在管道中的流动,牛 奶、果汁、糖浆等在管道中的流动等。 本节主要讨论管中不可压缩流体的运动规律,其中介绍层流和紊流的概念 讨论层流和紊流能量损失的形成原因和计算方法,介绍沿程阻力和局部阻力系数 的计算公式及图表。 4.1管中稳定流动连续性方程 稳定流动情况下,单位时间内流进体系的流体质量等于流出体系的流体质 量,即 P1u1A1=p2u2A2 (1-32) 式中:P1、P2为管段两端面处的流体密度,kgm3;u1、u2为管段两端面处的 平均流速,m/s;A1、A2为管段两端的横截面面积,m。 式(1-32)称为流体在管中稳定流动时的连续性方程。对于不可压缩流体, 由于P1=p2,式(1-32)改为 u1A1=u2A2 (1-33) 该式表明,不可压缩流体的平均流速,其数值只随管道截面面积变化,流速 与管径平方成反比
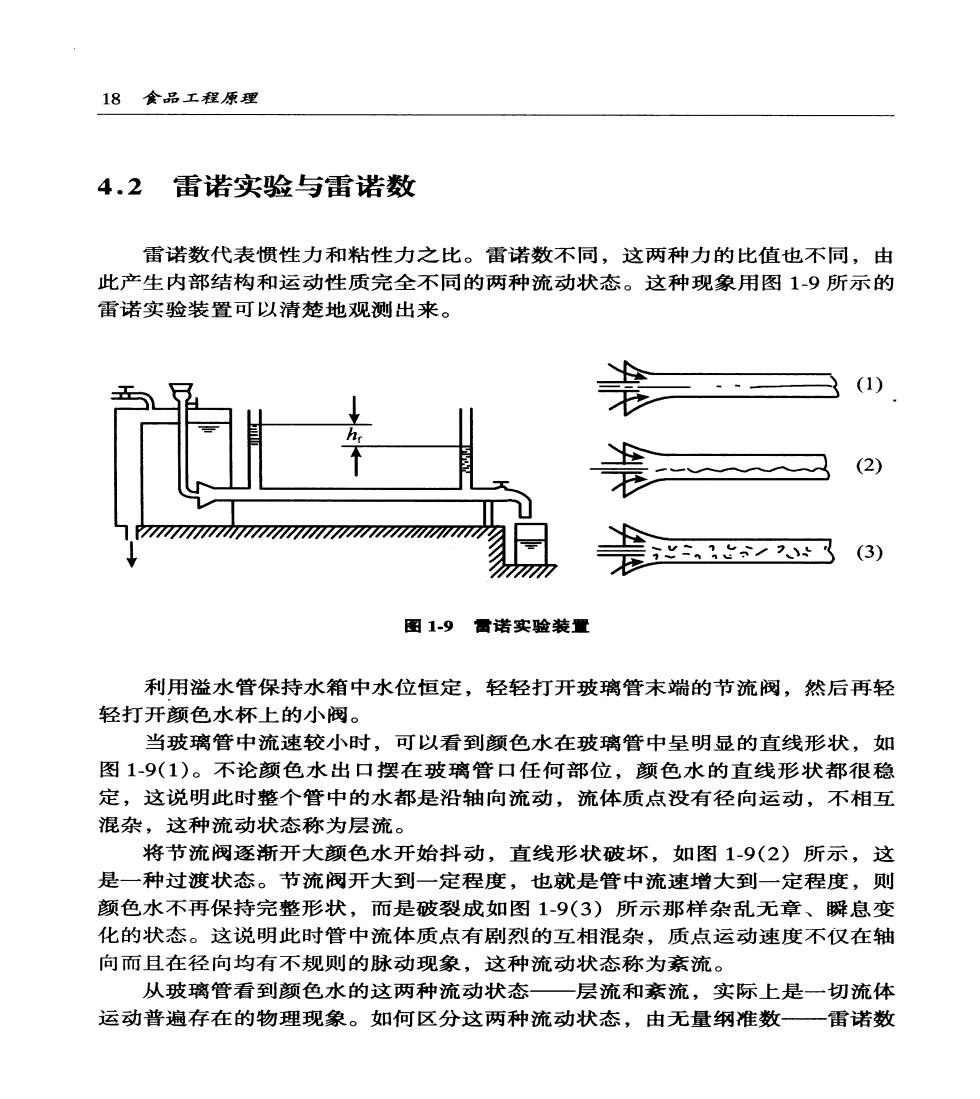
18食品工程原理 4.2雷诺实验与雷诺数 雷诺数代表惯性力和粘性力之比。雷诺数不同,这两种力的比值也不同,由 此产生内部结构和运动性质完全不同的两种流动状态。这种现象用图1-9所示的 雷诺实验装置可以清楚地观测出来。 (1) (2) ,出1一☒ (3) 图1-9雷诺实验装置 利用溢水管保持水箱中水位恒定,轻轻打开玻璃管末端的节流阀,然后再轻 轻打开颜色水杯上的小阀。 当玻璃管中流速较小时,可以看到颜色水在玻璃管中呈明显的直线形状,如 图1-9(1)。不论颜色水出口摆在玻璃管口任何部位,颜色水的直线形状都很稳 定,这说明此时整个管中的水都是沿轴向流动,流体质点没有径向运动,不相互 混杂,这种流动状态称为层流。 将节流阀逐渐开大颜色水开始抖动,直线形状破坏,如图1-9(2)所示,这 是一种过渡状态。节流阀开大到一定程度,也就是管中流速增大到一定程度,则 颜色水不再保持完整形状,而是破裂成如图1-9(3)所示那样杂乱无章、瞬息变 化的状态。这说明此时管中流体质点有剧烈的互相混杂,质点运动速度不仅在轴 向而且在径向均有不规则的脉动现象,这种流动状态称为紊流。 从玻璃管看到颜色水的这两种流动状态—层流和紊流,实际上是一切流体 运动普遍存在的物理现象。如何区分这两种流动状态,由无量纲准数一雷诺数

第1章流体力学基础19 Re来判断。雷诺数Re的表达式 Re=lup (1-34) 式中:l为特征尺寸,m;u为流体平均速度,ms;p为流体密度,kgm3;u 为流体动力粘度,Pa·s。 流态稳定性的判断标准为: Re>4000时,管中流动状态一般都为紊流; Re<2000时,管中流动状态都为层流。 2000<Re<4000时,管中流动状态可为层流,也可能为紊流,但紊流的 可能性更大。原因是在雷诺数较高时层流极不稳定,遇到外界振动干扰就容易变 为紊流。因此,层流与紊流的判断标准有时简化为: Re<2000时,管中流动状态为层流; Re>4000时,管中流动状态为紊流。 4.3水力直径 一般雷诺数R=2中的特征尺寸1在圆形管道中取直径d,因而圆管的雷 诺数是Re=P,但在异形管道中用什么作为雷诺数中的特征尺寸呢? 我们看一下圆管直径与断面A和断面上流体与固体接触周长S的关系 93-4 πd=d 就可以受到启发。异形断面管道也可以用过流断面面积A与过流断面上流体与 固体接触周长S之比的4倍来作为特征尺寸。这种尺寸称为水力直径,用dH表 示 d=4 (1-35) 于是异形管道的雷诺数为Re=HE。 根据实验,几种异形管道层流紊流的判断标准列于表1-3

20食品工程原理 表13异形管道的雷诺数及判断标准 正方形 正三角形 圆心缝隙 偏心缝隙 管道断面形状 P-a- Re-y du 光a “分 26 (D- 层流Re.< 2070 1930 1100 1000 4.4圆管中的层流 4.4.1速度分布与流量 如图1-10所示,取半径为x、长度为L的一个圆柱体,在稳定流动中这个 圆柱体处于平衡状态,因而作用在圆柱体上的外力在x方向(轴向)的投影和 为零。此种外力有二:一为两端面上的压力(p1一p2)π2;二为圆柱面上的摩 擦力x2πl,于是由∑F.=0,可得 (p1-p2)rr2-x2xl=0 简化并引用牛顿内摩擦定律r=一:,可得 =-2,=品 (1-36) 很明显,上式仅适用于稳定、单向、轴对称、等径均匀的流体流动情况。对上式 进行积分 au+了0dr -△2(R2-2) u=Aul (1-37)