
21藏 第4章 食品系列数材 颗粒与流体之间的 相对流动 本章的学习目的与要求 学习本章内容,学生能够掌握颗粒与流体相对运动的基本 理论,为食品流化加工、沉降分离加工等工艺设计、设备选型 提供原理知识。要求学生掌握流体绕过颗粒以及颗粒在流体中 沉浮的速度和阻力计算方法;能够分析并处理流化加工、气力 输送、沉降和过滤中的工程实际问题

268食品工程原理 颗粒与流体之间的相对流动可以有以下几种情况:①颗粒静止,流体绕过颗 粒及颗粒床层的流动,如混浊的水经过砂粒床层、悬浮液经过滤介质的过滤,溶 液经过离子交换树脂床层的流动,以及气体经过固定床层的流动等。液体以曳力 作用于颗粒,颗粒对流体的流动产生阻力。曳力与阻力的关系是作用力与反作用 力的关系。流动的实质是将流体经过众多固体颗粒所组成的不规则通道的流动看 成流体经过众多毛细管或类似毛细管的孔隙间的流动,大多数情况下是滞流状态 下的流动。②颗粒运动,流体静止或处于某种运动。在重力场中,只要固体颗粒 的密度大于流体的密度,固体颗粒将在重力方向上与流体作相对运动;在离心场 中,则与流体作离心力方向上的相对运动:如a.两相物系的沉降分离;b.流 固两相之间进行某种物理和化学过程一固体物料的干燥、固体催化剂作用下的 化学反应等;c.固体颗粒的流动输送等等。 本章将先探讨颗粒与流体之间相对流动的基本规律,在此基础上,根据每一 特定操作各自的工艺特点,对流动现象进行不同的考察。 流体绕过颗粒及颗粒床层的流动 流体绕过颗粒的流动受颗粒特性和流体特性的影响;同理流体通过颗粒床层 的流动受颗粒床层特性和流体特性的影响,但颗粒床层是由大量尺寸不等、形状 也不规则的固体颗粒随机堆积而成,颗粒层内的流体通道具有复杂的网状结构。 故描述这样的复杂通道应从组成通道的颗粒特性着手。 当流体通过众多固体颗粒堆积而成的颗粒床层时,如果颗粒静止不动,该床 层就称为固定床(stationary/stabilized bed)。许多食品工业操作都与流体通过固 定床的流动有关,如固定化生产酶制剂,果汁、蔬菜汁及葡萄糖和味精生产中的 含品液体等悬浮液的过滤等等。 1.1颗粒床层的特性 1.1.1单颗粒的特性 主要是颗粒的大小(体积)、形状和表面积

第4章颗粒与流体之间的相对流动269 球形颗粒(spherical particle)众所周知,球形颗粒的直径为d。时,其体积 V(olume)和表面积S(surface area)分别为: v-r (4-1) S=πd3 (4-2) 因此,球形颗粒的各有关特性可用单一参数一直径d。全面表示。 另外,引入比表面积a(specific surface area)的概念,即将单位体积固体颗 粒所具有的表面积称为颗粒的比表面。以此表征颗粒表面积的大小,则球形颗粒 的比表面: a球=号=合。 (4-3) 非球形颗粒(non-spherical particle)工业所遇到的固体颗粒大多是非球形的。 非球形颗粒的形状千变万化,通常试图将非球形颗粒以某种当量的球形颗粒代 表,以使所考察的领域内非球形颗粒的特性与球形颗粒等效,这一球的直径称为 当量直径(equivalent diameter).。例:质量等效或体积等效的当量直径常用于研 究颗粒在重力(或离心力)场中所受的场力;而比表面积当量直径常用于探讨流 体通过颗粒层的流动阻力,因为影响该阻力的主要颗粒特性是颗粒的比表面积。 据不同方面的等效性,可定义不同的当量直径。 (①)体积等效使当量球形颗粒的体积x零等于真实颗粒的体积V,则体 积当量直径(equivalent volume diameter)定义为: do-Vov (4-4) (2)表面积等效使当量球形颗粒的表面积πd名等于真实颗粒的表面积S, 则面积当量直径(equivalent surface diameter)定义为: d=√A (4-5) (3)比表面积等效使当量球形颗粒的比表面积等于真实颗粒的比表面 积a,则比表面积当量直径(equivalent specific surface diameter)定义为: d=8-g (4-6)

270食品工程原理 显然以上3个当量直径之间有如下关系: d-是-经d d2 (4-7) de=pade=psl5 de (4-8) 仰的物理含义为 一器一登-生政绿装装数面我 非球形颗粒的表面积 可称为形状系数(form/Shape coefficient)或球形度(sphericity),即形状系 数等于与颗粒等体积的球形粒子的表面积与颗粒的实际表面积之比。体积相同时 球形颗粒的表面积最小,因此,任何非球形颗粒的形状系数皆小于1。 综上所述,对球形颗粒,以一个参数即颗粒直径d。便可惟一确定其体积、 表面积和比表面积;对非球形颗粒,则必须定义两个参数才能确定其体积、表面 积和比表面积。若定义体积当量直径dw(以下简写为d。),则有 V=r明 (4-9) 6 S-r经 (4-10) a=psde 6 (4-11) 1.1.2颗粒群的特性 任何颗粒群中,其单颗粒的尺寸都不可能完全一样,从而形成一定的尺寸 (粒度)分布,即任何颗粒群具有某种粒度分布(particle size distributions)。为 研究颗粒分布对颗粒层内流动的影响,首先必须设法测量并定量这一分布。颗粒 粒度(particle size)测量的方法有筛分法(sieve method)、显微镜法(microsoopic method、沉降法(sedimentation)、电阻变化法(measuring resistance strain/varian- ce)、光散射与衍射法(light diffusion and diffraction methods)、表面积法(specific surface method)等等。它们各自基于不同的原理,适用于不同的粒径范围,所得的 结果也往往略有不同
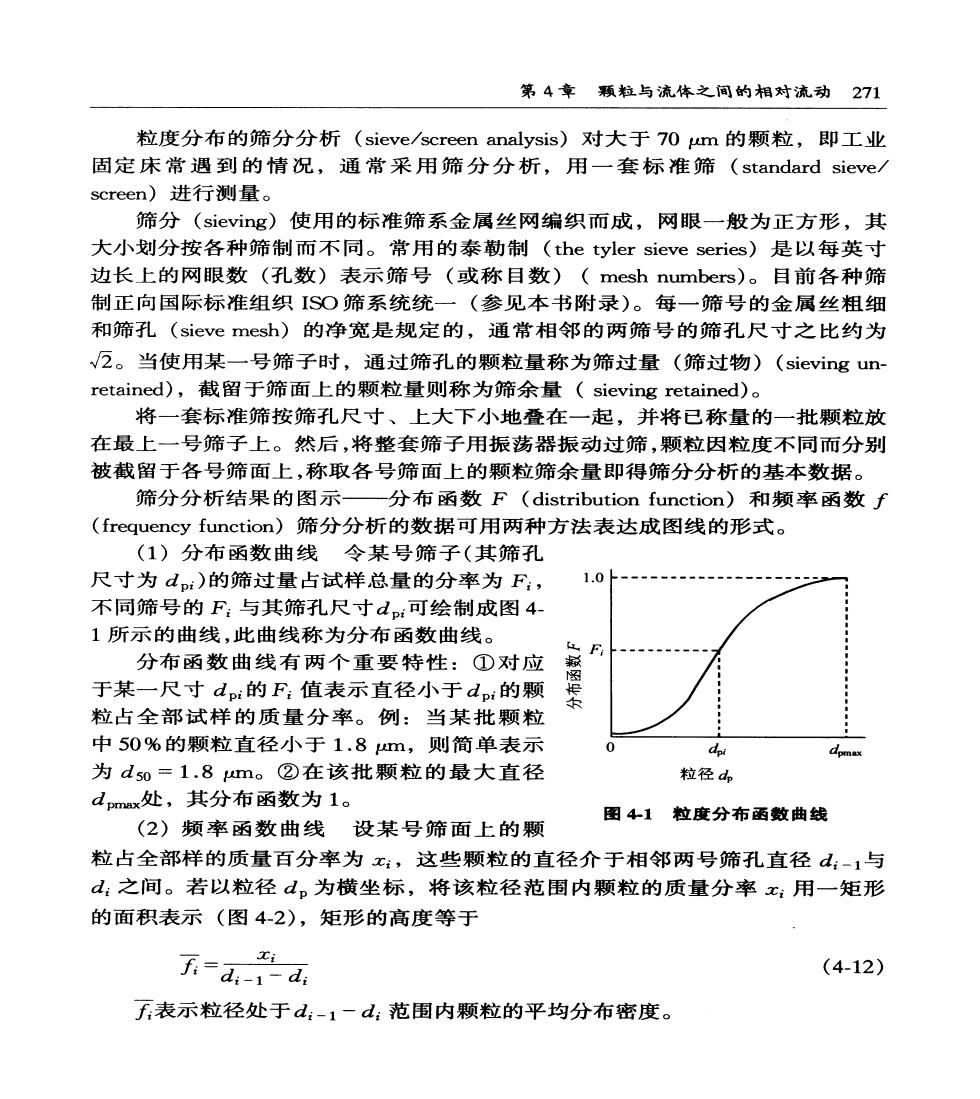
第4章颗粒与流体之间的相对流动271 粒度分布的筛分分析(sieve/screen analysis)对大于70m的颗粒,即工业 固定床常遇到的情况,通常采用筛分分析,用一套标准筛(standard sieve,/ screen)进行测量。 筛分(sieving)使用的标准筛系金属丝网编织而成,网眼一般为正方形,其 大小划分按各种筛制而不同。常用的泰勒制(the tyler sieve series)是以每英寸 边长上的网眼数(孔数)表示筛号(或称目数)(mesh numbers)。目前各种筛 制正向国际标准组织ISO筛系统统一(参见本书附录)。每一筛号的金属丝粗细 和筛孔(sieve mesh)的净宽是规定的,通常相邻的两筛号的筛孔尺寸之比约为 √2。当使用某一号筛子时,通过筛孔的颗粒量称为筛过量(筛过物)(sieving un- retained),截留于筛面上的颗粒量则称为筛余量(sieving retained)。 将一套标准筛按筛孔尺寸、上大下小地叠在一起,并将已称量的一批颗粒放 在最上一号筛子上。然后,将整套筛子用振荡器振动过筛,颗粒因粒度不同而分别 被截留于各号筛面上,称取各号筛面上的颗粒筛余量即得筛分分析的基本数据。 筛分分析结果的图示 -分布函数F(distribution function)和频率函数f (frequency function)筛分分析的数据可用两种方法表达成图线的形式。 (1)分布函数曲线令某号筛子(其筛孔 尺寸为dp)的筛过量占试样总量的分率为F:, 1.0 不同筛号的F:与其筛孔尺寸dp可绘制成图4 1所示的曲线,此曲线称为分布函数曲线。 分布函数曲线有两个重要特性:①对应 于某一尺寸dp:的F:值表示直径小于dp:的颗 粒占全部试样的质量分率。例:当某批颗粒 中50%的颗粒直径小于1.8m,则简单表示 为dso=1.8m。②在该批颗粒的最大直径 粒径4 d pmax处,其分布函数为1。 图41粒度分布函数曲线 (2)频率函数曲线设某号筛面上的颗 粒占全部样的质量百分率为x,这些颗粒的直径介于相邻两号筛孔直径d:-1与 d:之间。若以粒径d。为横坐标,将该粒径范围内颗粒的质量分率x:用一矩形 的面积表示(图4-2),矩形的高度等于 i f=d-1-d: (4-12) f表示粒径处于d:-1-d:范围内颗粒的平均分布密度