
3.2对偶价格和递减成本之间的经济关系 3.2.2对偶价格,拉格郎日乘数,KKT条件和活 动成本估算 当你用LNGO求解一个连续型最优化模型时, 对于任意一个约束你都可以找到相应的对偶价格。 为了简单起见,我们假设目标函数是最大化,所 有的约束都是小于等于类型,而且所有的变量都 在约束的左边。一个约束的对偶价格是约束右边 常数变动一个单位时目标函数值变动的数量。 13
13 3.2对偶价格和递减成本之间的经济关系 3.2.2 对偶价格,拉格郎日乘数,KKT 条件和活 动成本估算 当你用LINGO求解一个连续型最优化模型时, 对于任意一个约束你都可以找到相应的对偶价格。 为了简单起见,我们假设目标函数是最大化,所 有的约束都是小于等于类型,而且所有的变量都 在约束的左边。一个约束的对偶价格是约束右边 常数变动一个单位时目标函数值变动的数量

3.2对偶价格和递减成本之间的经济关系 这个结论还是来自关于等式约束的拉格朗日 乘数的概念。拉格朗日乘数概念已经有了100多年 的历史。为了说明问题,我们来考察下面的非线 性问题,它与前面的问题略有不同 [ROW1] MAX 40*(X+1)^0.5+30*(Y+1)^.5+25*(z+1)^.5: [ROW2 X 15*z <= 45; [ROW3] <=45; [ROW4] X*X+3*Y*Y+9 *Z*Z <= 3500:
14 3.2对偶价格和递减成本之间的经济关系 这个结论还是来自关于等式约束的拉格朗日 乘数的概念。拉格朗日乘数概念已经有了100多年 的历史。为了说明问题,我们来考察下面的非线 性问题,它与前面的问题略有不同: [ROW1] MAX = 40*(X+l)^0.5 + 30*(Y+l)^.5 + 25*(Z+1)^.5; [ROW2] X + 15*Z <= 45; [ROW3] y + Z <= 45; [ROW4] X*X + 3*Y*Y + 9 *Z*Z <= 3500;

3.2对偶价格和递减成本之间的经济关系 我们省略了约束X,Z>=0。 求解模型以后可得下面的解答 Local optimal solution found at step:7 Objective value: 440.7100 Variable Value Reduced Cost X 45.00000 0.0000000 Y 22.17356 0.0000000 0.0000000 0.1140319 15
15 3.2对偶价格和递减成本之间的经济关系 我们省略了约束X, Y, Z >= 0。 求解模型以后可得下面的解答: Local optimal solution found at step: 7 Objective value: 440.7100 Variable Value Reduced Cost X 45.00000 0.0000000 Y 22.17356 0.0000000 Z 0.0000000 0.1140319
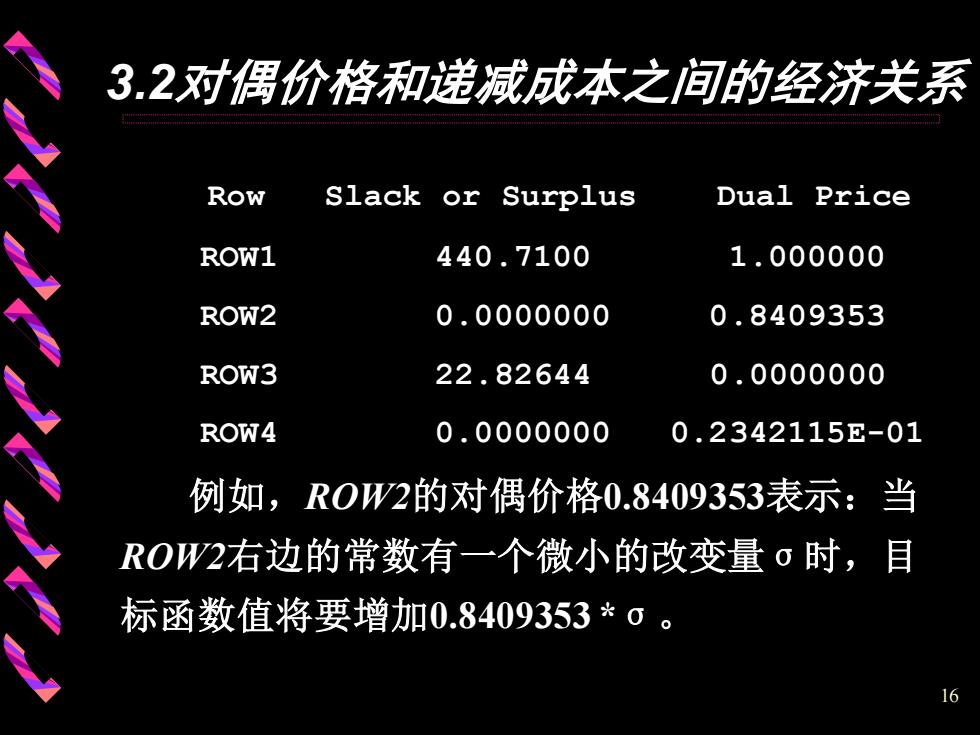
3.2对偶价格和递减成本之间的经济关系 Row slack or Surplus Dual Price ROW1 440.7100 1.000000 ROW2 0.0000000 0.8409353 ROW3 22.82644 0.0000000 ROW4 0.0000000 0.2342115E-01 例如,R0W2的对偶价格0.8409353表示:当 ROW2右边的常数有一个微小的改变量·时,目 标函数值将要增加0.8409353*σ 16
16 3.2对偶价格和递减成本之间的经济关系 Row Slack or Surplus Dual Price ROW1 440.7100 1.000000 ROW2 0.0000000 0.8409353 ROW3 22.82644 0.0000000 ROW4 0.0000000 0.2342115E-01 例如,ROW2的对偶价格0.8409353表示:当 ROW2右边的常数有一个微小的改变量σ时,目 标函数值将要增加0.8409353 *σ

3.2对偶价格和递减成本之间的经济关系 当我们试图去理解为什么一个变量取0值或 者一个活动为什么未被使用的时候,一个很有用 的方法就是全面地估算这个活动的成本。为了说 明变量对目标函数的贡献,我们给出变量“信用 这个概念,它用每一个约束增量的加权和表示。 这里的权数就是约束的对偶价格。约束的增量就 是约束左边关于变量的导数。关于变量Z的全面 估算说明如下 17
17 3.2对偶价格和递减成本之间的经济关系 当我们试图去理解为什么一个变量取0值或 者一个活动为什么未被使用的时候,一个很有用 的方法就是全面地估算这个活动的成本。为了说 明变量对目标函数的贡献,我们给出变量“信用” 这个概念,它用每一个约束增量的加权和表示。 这里的权数就是约束的对偶价格。约束的增量就 是约束左边关于变量的导数。关于变量Z的全面 估算说明如下: