3.2对偶价格和递减成本之间的经济关系 Row 关于Z的偏导数值 Dual price 乘积 ROW1 12. -1 -12.5 ROW2 15 0.8409353 12.61403 ROW3 0 ROW4 0.02342115 0 净值(递减成本):0.11403 18
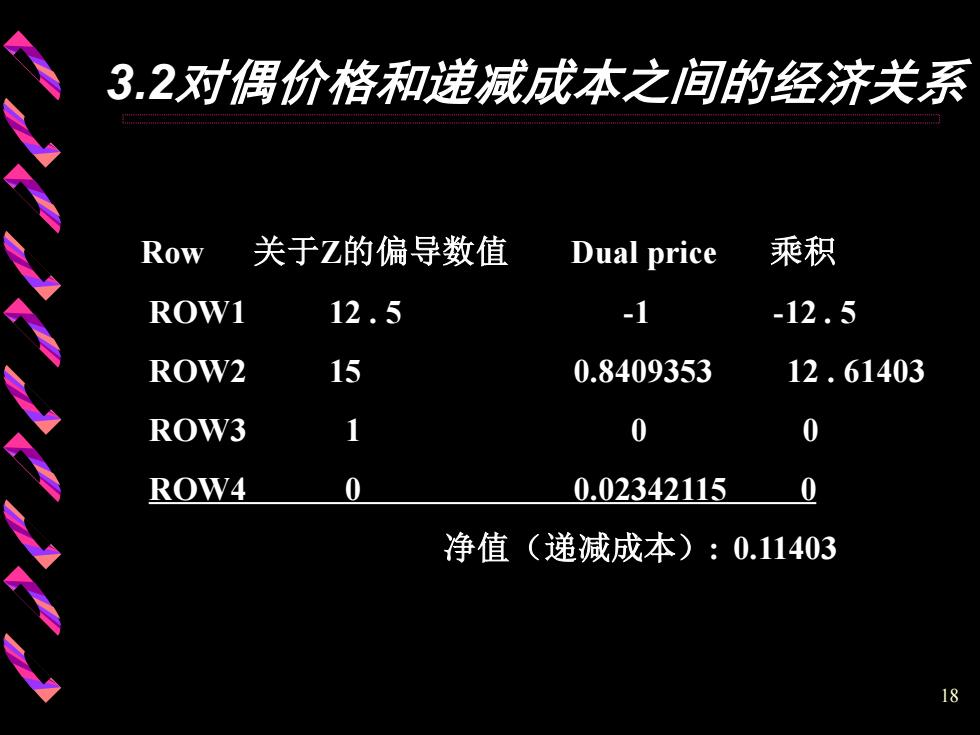
18 3.2对偶价格和递减成本之间的经济关系 Row 关于Z的偏导数值 Dual price 乘积 ROW1 12 . 5 -1 -12 . 5 ROW2 15 0.8409353 12 . 61403 ROW3 1 0 0 ROW4 0 0.02342115 0 净值(递减成本): 0.11403
3.2对偶价格和递减成本之间的经济关系 另一方面,如果我们对变量X进行全面地成 本估算,我们会得到 Row 关于X的偏导数值 对偶价格 乘积 ROW1 2.9488391 -2.9488391 ROW2 0.8409353 0.8409353 ROW3 0 0 ROW4 90 0.02342115 2.107899 净值(递减成本):0 19
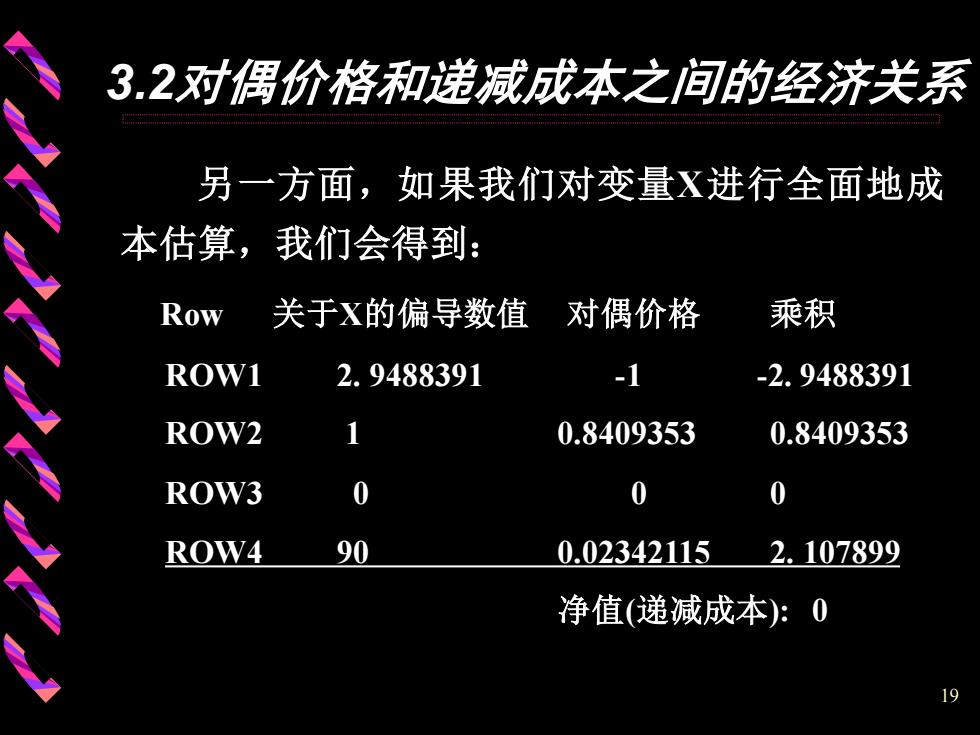
19 3.2对偶价格和递减成本之间的经济关系 另一方面,如果我们对变量X进行全面地成 本估算,我们会得到: Row 关于X的偏导数值 对偶价格 乘积 ROW1 2. 9488391 -1 -2. 9488391 ROW2 1 0.8409353 0.8409353 ROW3 0 0 0 ROW4 90 0.02342115 2. 107899 净值(递减成本): 0

3.2对偶价格和递减成本之间的经济关系 这两个计算结果说明了下面的KKT条件 Karush/Kuhn/Tucker) a)如果一个变量有正值的递减成本,则它的 值一定是0; b)如果一个变量被使用了(就是值大于0): 则它的递减成本值一定是0; 20
20 3.2对偶价格和递减成本之间的经济关系 这两个计算结果说明了下面的 KKT 条件 (Karush/Kuhn/Tucker) : a) 如果一个变量有正值的递减成本 ,则它的 值一定是0; b) 如果一个变量被使用了 (就是值大于0), 则它的递减成本值一定是0;

3.2对偶价格和递减成本之间的经济关系 C)如果一个小于等于类型约束的对偶价格大 于0,则它的缺损(松弛)值一定是0; d)如果一个小于等于类型约束的缺损 (松弛) 值大于0,则它的对偶价格一定是0。 这些性质有时也称为互补松弛性 21
21 3.2对偶价格和递减成本之间的经济关系 c) 如果一个小于等于类型约束的对偶价格大 于0,则它的缺损(松弛)值一定是0; d) 如果一个小于等于类型约束的缺损(松弛) 值大于0,则它的对偶价格一定是0。 这些性质有时也称为互补松弛性

3.3递减成本和对偶价格的变化范围 3.3递减成本和对偶价格的变化范围 在前面解释递减成本和对偶价格的过程中, 我们限制改变量只有微小的变化或一个单位。例 如,如果一个约束的对偶价格$3/小时,在最初的 数小时(可能不到1小时)内,每增加1小时总利 润将增加$S3。当然,一般情况下这一增长的比例 不会保持不变。你也许想知道:当增量为多少小 时的时候,它们的对偶价格不再增加或开始减少? 并不是什么情况都会发生 22
22 3.3 递减成本和对偶价格的变化范围 3.3 递减成本和对偶价格的变化范围 在前面解释递减成本和对偶价格的过程中, 我们限制改变量只有微小的变化或一个单位。例 如,如果一个约束的对偶价格$3/小时,在最初的 数小时(可能不到1小时)内,每增加1小时总利 润将增加$3。当然,一般情况下这一增长的比例 不会保持不变。你也许想知道:当增量为多少小 时的时候,它们的对偶价格不再增加或开始减少? 并不是什么情况都会发生