
二、方差分析的作用 >解决多个处理的比较问题,充分利用资 料的全部信息,提高分析的精确度。 1、在单因素试验中,可以分辨出最优的水平。 2、在多因素试验中,可以分辨出最优的水平组合。 W
1、在单因素试验中,可以分辨出最优的水平。 2、在多因素试验中,可以分辨出最优的水平组合。 二、方差分析的作用 ➢ 解决多个处理的比较问题,充分利用资 料的全部信息,提高分析的精确度

&7.2方差分析及基本原理 方差分析的概念: 变异原因的数量分析 》将试验数据的总变异分解为不同来源 的变异,从而评定不同变异来源的相对重要 性的一种统计方法。 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 方差分析的概念: 变异原因的数量分析 将试验数据的总变异分解为不同来源 的变异,从而评定不同变异来源的相对重要 性的一种统计方法。 &7.2 方差分析及基本原理

一、数据结构与与变异来源的分解 设有k个处理,每个处理有个 观察值,则共有k个观察值,其数 据结构和符号如表7.1
设有k个处理,每个处理有n个 观察值,则共有nk个观察值,其数 据结构和符号如表7.1。 一、数据结构与变异来源的分解

表7.1K个处理n个观察值的符号表 处理 1 2 i.K 1 X11 X21.Xi1.Xk1 2 X12 X22 .X2.Xk2 j X1j X2j X对.X对 D 8 8n8 n Xin X2n .Xin. Xkn 总和 T1 T2 Ti .Tk T=∑,=∑7 平均 , 元.4 均方 s s 。S
表7.1 K个处理n个观察值的符号表 处理 1 2 . i . k 1 x11 x21 . xi1 . xk1 2 x12 x22 . xi2 . xk2 : : : . :. : j x1j x2j . xij . xkj : : :. :. : n x1n x2n . xin . xkn 总和 T1 T2 . Ti . Tk 平均 . . 均方 . . 1 x 2 x i x k x 2 1 s 2 2 s 2 i s 2 k s kn x x T x T ij ij i = = =
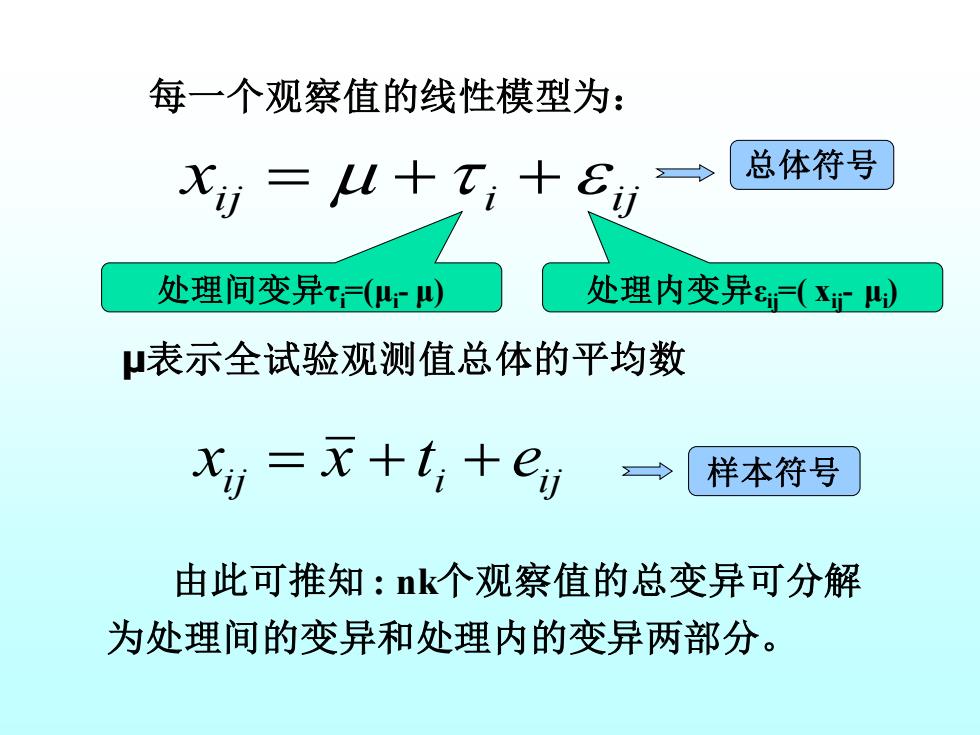
每一个观察值的线性模型为: Xi=L+T;+E→ 总体符号 处理间变异() 处理内变异(X山 μ表示全试验观测值总体的平均数 xj=元+t+e 样本符号 由此可推知:k个观察值的总变异可分解 为处理间的变异和处理内的变异两部分
每一个观察值的线性模型为: 处理间变异τi=(μi - μ) 处理内变异εij=( xij- μi ) 由此可推知 : nk个观察值的总变异可分解 为处理间的变异和处理内的变异两部分。 i j i i j x = + + 总体符号 i j i i j x = x + t + e 样本符号 μ表示全试验观测值总体的平均数