章 第六章卡平方测验 课时 2 &6.1卡平方测验概述 节 &6.2 适合性测验 &6.3独立性测验 教学 (①)了解卡平方的定义及其分布特点:(2)掌握次数资料的适合性测验和 目 独立性测验方法。 1.掌握次数资料的适合性测验法 教学 2.掌握次数资料的独立性测验,尤其2×2联列表x2测验 重点 1.x独立测验用基本公式时,各观测值相应理论值的计算。 教学 突破方法: 难点 举例说明,再总结出规律,总结求理论值的通式。主张用独立测验 的简化公式,举例说明公式中每个符号的含义,以便正确应用公式。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钧钻主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中因农业出版社,2007。 3. 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985 6 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10.《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11.《试验设计与分析》,袁志发主编,高等教有出版社,2000
1 章 第六章 卡平方测验 课时 2 节 &6.1 卡平方测验概述 &6.2 适合性测验 &6.3 独立性测验 教学 目的 (1)了解卡平方的定义及其分布特点;(2)掌握次数资料的适合性测验和 独立性测验方法。 教学 重点 1. 掌握次数资料的适合性测验法 2. 掌握次数资料的独立性测验,尤其 2×2 联列表 x 2 测验。 教学 难点 1. x 2 独立测验用基本公式时,各观测值相应理论值的计算。 突破方法: 举例说明,再总结出规律,总结求理论值的通式。主张用 x 2 独立测验 的简化公式,举例说明公式中每个符号的含义,以便正确应用公式。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11. 《试验设计与分析》,袁志发主编,高等教育出版社,2000
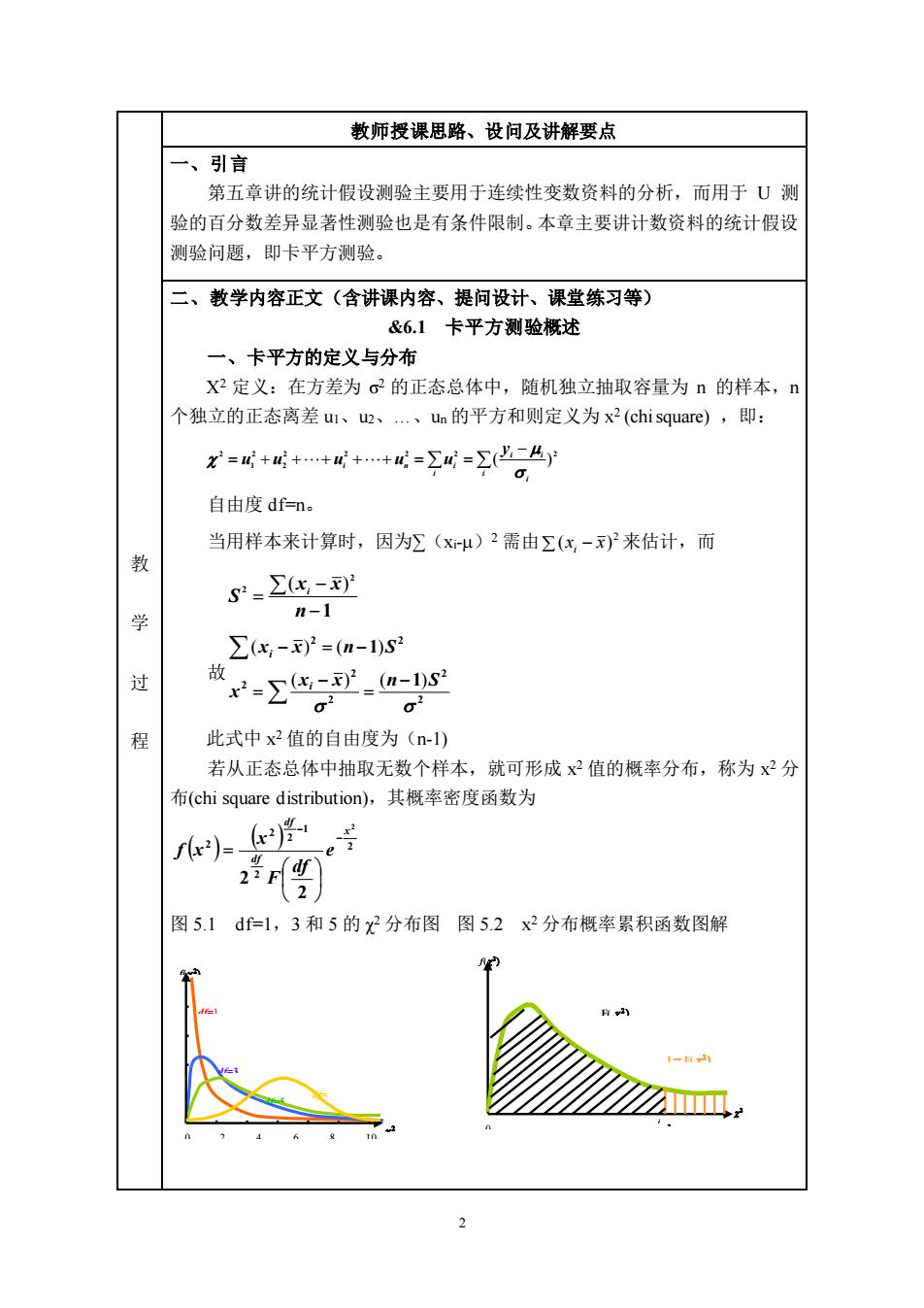
教师授课思路、设问及讲解要点 ,引言 第五章讲的统计假设测验主要用于连续性变数资料的分析,而用于U测 验的百分数差异显著性测验也是有条件限制。本章主要讲计数资料的统计假设 测验问题,即卡平方测验 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &6.1卡平方测验概述 一、卡平方的定义与分布 X2定义:在方差为c2的正态总体中,随机独立抽取容量为n的样本,n 个独立的正态离差uI、m的平方和则定义为x2(chisquare),即: 父=+G++度++成=2=y心二4 自由度dfm。 当用样本来计算时,因为∑(xμ)2需由Σ(化-)来估计,而 教 s=2s- n-1 ∑(x,-2=(m-1S2 过 -。.as 程 此式中x2值的自由度为(n-l) 若从正态总体中抽取无数个样本,就可形成x2值的概率分布,称为x2分 布(chi square distribution),其概率密度函数为 图5.1df=1,3和5的2分布图图52x2分布概率累积函数图解
2 教 学 过 程 教师授课思路、设问及讲解要点 一、引言 第五章讲的统计假设测验主要用于连续性变数资料的分析,而用于 U 测 验的百分数差异显著性测验也是有条件限制。本章主要讲计数资料的统计假设 测验问题,即卡平方测验。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &6.1 卡平方测验概述 一、卡平方的定义与分布 X2 定义:在方差为 σ 2 的正态总体中,随机独立抽取容量为 n 的样本,n 个独立的正态离差 u1、u2、.、un 的平方和则定义为 x 2 (chi square) ,即: 自由度 df=n。 当用样本来计算时,因为∑(xi-)2 需由 2 (x x) i − 来估计,而 故 2 2 2 2 2 2 2 1 1 x x n S x x x n S i i ( ) ( ) ( ) ( ) − = − = − = − 此式中 x 2 值的自由度为(n-1) 若从正态总体中抽取无数个样本,就可形成 x 2 值的概率分布,称为 x 2 分 布(chi square distribution),其概率密度函数为 ( ) ( ) 2 2 1 2 2 2 2 2 2 x df df e df F x f x − − = 图 5.1 df=1,3 和 5 的 χ 2 分布图 图 5.2 x 2 分布概率累积函数图解 − = + + + + + = = i i i i i i n i y u u u u u 2 2 2 2 2 2 2 1 2 ( ) 1 2 2 − − = n x x S i ( ) df=1 0 2 4 6 8 10 12 f( ) df=3 df=5 df= ∞ f( ) 0 F( ) 1-F( ) i

x2分布的特性有: ()x2分布的取值范围为0,+o0) (2x2分布的形状决定于自由度df。(图5.1)。 (3)x2分布曲线与横坐标轴所围成的面积等于1,即 p(0sx'(+)=[f(x'H(x')=1 x2分布的累积函数F(c2为F()=pk≤x》=f儿6) 二、x2测验公式 K.Pearson(1900)根据的x2上述定义从属性性状的分布推导出用于次数资 料(亦称计数资料)分析的x2公式: X心的基本公式:X=∑0-团 当d=1的样本,必须用连续性矫正公式:当d企2时,可以不作连续性矫 正。 火连续性桥正公式:心-Σ0-)-立 E 三、x2测验的应用 过 用于适合性测验:用于独立性测验:用于方差同质测验 四、x2测验的具体步骤 程 (1)提出无效假设与备择假设 (②)确定显著水平确定a=0.05或0.01等。 (3)计算x2值 由样本资料和理论假设计算 x2值:根据自由度,由附表4查出x2dF。 (4)推断,若X2≤2adf,则p>a,故接受Ho: Xadf,则p<a,故否定Ho: 卡平方测验均为一尾测验,且是右尾测验。 三、卡平方测验的连续性矫正 x2是连续分布,而次数资料是间断性的,由间断性资料计算的x2值均有 不同程度偏大的趋势,尤其在=1时偏差较大。为此,需对x2进行连续性矫 正使之符合x2的理论分布: x=Σ0-E-0 当d>2时,可以不作连续性矫正
3 教 学 过 程 x 2 分布的特性有: ⑴ x 2 分布的取值范围为[0,+∞)。 ⑵x 2 分布的形状决定于自由度 df。(图 5.1)。 ⑶ x 2 分布曲线与横坐标轴所围成的面积等于 1,即 (0 ) ( ) ( ) 1 2 0 2 2 + = = + p x f x d x x 2 分布的累积函数 F( c2)为 ( ) ( ) ( ) ( ) 2 0 2 2 2 2 2 d x x F x p x f x i xi = = 二、x 2 测验公式 K.Pearson(1900)根据的 x 2 上述定义从属性性状的分布推导出用于次数资 料(亦称计数资料)分析的 x 2 公式: X2 的基本公式: − = i E O E 2 2 ( ) 当 df=1 的样本,必须用连续性矫正公式;当 df≥2 时,可以不作连续性矫 正。 X2 连续性矫正公式: − − = E O E xc 2 2 ] 2 1 [( ) 三、 x 2 测验的应用 用于适合性测验;用于独立性测验;用于方差同质测验 四、 x 2 测验的具体步骤 ⑴ 提出无效假设与备择假设 ⑵ 确定显著水平 确定 a=0.05 或 0.01 等。 ⑶ 计算 x 2 值 由样本资料和理论假设计算 x 2 值;根据自由度,由附表 4 查出 x 2 a,df 。 ⑷ 推断,若 χ 2≤χ2 a.df,则 p>α,故接受 H0; χ 2≥χ2 a.df ,则 p<α,故否定 H0; 卡平方测验均为一尾测验,且是右尾测验。 三、卡平方测验的连续性矫正 x 2 是连续分布,而次数资料是间断性的,由间断性资料计算的 x 2 值均有 不同程度偏大的趋势,尤其在 df=1 时偏差较大。为此,需对 x 2 进行连续性矫 正使之符合 x 2 的理论分布: ] ( . ) [ − − = E O E xc 2 2 0 5 当 df≥2 时,可以不作连续性矫正

&6.2适合性测验 根据x2分布的概率值来判断实际次数与预期理论次数是否符合的假设测 验,称为适合性测验(goodness test)。 测验实际结果与理论比例是否符合 测验产品质量是否合格: 测验实验结果是否符合某一理论分布: 【例7.1】孟德尔(1865)将黄子叶饱满豌豆与绿子叶皱缩豌豆杂交,下2代 观察556株,黄子叶饱满315株,黄子叶皱缩101株,绿子叶饱满108株,绿 子叶皱缩32株。试测验F2代的分离是否符合93:3:1的理论比率。 豌豆杂种F2代性状分离的观察次数与理论次数(=556) 次数 黄子叶饱满黄子叶皱缩绿子叶饱满绿子叶皱缩 实际次数(0)315 101 108 32 理论次数(E)312.75104.25 104.25 34.75 假设Ho:F2代的分离符合93:3:1的理论比率, 学 HA:F2代的分离不符合93:31的理论比率 显著水平a=0.05。 x-315-3275+01-10425,108-10425,62-3475 312.75 104.25 104.25 34.75 程 =0.470 dfk-1=41=3,由附表4查出x2o.0s.3=7.815。 x2<x305.3,不能否定H0,认为豌豆杂种F2代的分离是符合93:3:1 的理论比率。 【例7.2】有一批水稻种子,规定发芽率达80%合格,即发芽:不发芽=41 随机抽200粒做发芽试验,发芽种子数为150粒。这批水稻种子是否合格? 假设H0:合格,即发芽:不发芽=4:1 c-o~E外0 E _150-160-05+050-0-05-228 160 40 df=k-1=2-1=1,由附表4查出x2005.1=3.84 结论:xe2<x2o.o5.1,不能否定H0,认为这批水稻种子是合格的
4 教 学 过 程 &6.2 适合性测验 根据 x 2 分布的概率值来判断实际次数与预期理论次数是否符合的假设测 验,称为适合性测验(goodness test)。 测验实际结果与理论比例是否符合; 测验产品质量是否合格; 测验实验结果是否符合某一理论分布; 【例 7.1 】孟德尔(1865)将黄子叶饱满豌豆与绿子叶皱缩豌豆杂交,F2 代 观察 556 株,黄子叶饱满 315 株,黄子叶皱缩 101 株,绿子叶饱满 108 株,绿 子叶皱缩 32 株。试测验 F2 代的分离是否符合 9:3:3:1 的理论比率。 豌豆杂种 F2 代性状分离的观察次数与理论次数(n=556) 次数 黄子叶饱满 黄子叶皱缩 绿子叶饱满 绿子叶皱缩 实际次数(O) 315 101 108 32 理论次数(E) 312.75 104.25 104.25 34.75 假设 H0: F2 代的分离符合 9:3:3:1 的理论比率, HA: F2 代的分离不符合 9:3:3:1 的理论比率。 显著水平 a=0.05 。 ( ) ( ) ( ) ( ) 0 470 34 75 32 34 75 104 25 108 104 25 104 25 101 104 25 312 75 315 312 75 2 2 2 2 2 . . . . . . . . . = − + − + − + − x = df=k-1=4-1=3,由附表 4 查出 x 2 0.05,3 =7.815 。 x 2<x 2 0.05,3 ,不能否定 H0 ,认为豌豆杂种 F2 代的分离是符合 9:3:3:1 的理论比率。 【例 7.2 】有一批水稻种子,规定发芽率达 80%合格,即发芽:不发芽=4:1。 随机抽 200 粒做发芽试验,发芽种子数为 150 粒。这批水稻种子是否合格? 假设 H0:合格,即发芽:不发芽=4:1 ( ) ( ) ( ) 2 28 40 50 40 0 5 160 150 160 0 5 0 5 2 2 1 2 2 . . . . = − − + − − = − − = = k i i i i c E O E x df=k-1=2-1=1,由附表 4 查出 x 2 0.05,1 =3.84 。 结论:x c 2< x 2 0.05,1 ,不能否定 H0 ,认为这批水稻种子是合格的

例7.5大豆花色一对等位基因的遗传研究,以紫花和白花的大豆品种杂交, 在F2代共得289株,其中紫花208株,白花81株。问这一资料的实际观察比 例是否符合于3:1的理论比值。 解:Ho:大豆花色F2分离符合3:1比率 由于该资料只有k=2组,v=k-1=1,故在计算x值时需作连续性矫正 0-)-打 x2=∑ E _(1-875-0.5}(8.75l-0.5} =0.3140+0.9420=1.2560 216.75 72.25 查表:X2005d-1F3.841X20.01dr1=6.635 现x2=1.2560<.1,故应接受H0,说明大豆花色这对性状是符合3: 比率。 结论:大豆花色符合一对等位基因的表型分离比例。 教 例:据以往的调查,消费者对3种不同原料的的满意度分别为0.45,0.31 学0.24。现随机选择60人评定该3种不同原料的饮料。从中选出各自最喜欢的 产品,结果分别为30人,18人,12人,试问消费者对3个新产品的态度是否 过 有改变? Ho:无改变 =∑0-Er -0.871 E x2-0.871<xos(2)=5.99,接受H0 结论:消费者对3个新产品的态度没有改变。 &6.3独立性测验 独立性测验(independence test)是测验两个变数之间是相互独立还是彼此 相关的统计方法,是次数资料的一种相关研究。 X2独立性其步骤和方法是: Ho:两个变数相互独立,HA:两个变数彼此相关。 将资料按两向分组排列成r行、c列的相依表(表5.3) X2基本公式或变形公式计算值 按自由度dfr-1(c-l)查表进行x2测验 写统计结论
5 教 学 过 程 例 7.5 大豆花色一对等位基因的遗传研究,以紫花和白花的大豆品种杂交, 在 F2 代共得 289 株,其中紫花 208 株,白花 81 株。问这一资料的实际观察比 例是否符合于 3∶1 的理论比值。 解:H0:大豆花色 F2 分离符合 3∶1 比率。 由于该资料只有 k=2 组, = k − 1 = 1 ,故在计算 2 值时需作连续性矫正。 − − = E O E xc 2 2 ] 2 1 [( ) 0.3140 0.9420 1.2560 72.25 ( |8.75|-0.5) 216.75 ( |-8.75|-0.5)2 2 = + = + = 查表:χ 2 0.05(df=1)=3.841 χ2 0.01(df=1)=6.635 现 =1.2560 2 C < 2 0.05,1 ,故应接受 H0,说明大豆花色这对性状是符合 3∶1 比率。 结论:大豆花色符合一对等位基因的表型分离比例。 例:据以往的调查,消费者对 3 种不同原料的的满意度分别为 0.45,0.31, 0.24。现随机选择 60 人评定该 3 种不同原料的饮料。从中选出各自最喜欢的 产品,结果分别为 30 人,18 人,12 人,试问消费者对 3 个新产品的态度是否 有改变? H0:无改变 − = E O E xc 2 2 [( )] =0.871 x 2=0.871< (2) 5.99 2 x0.05 = ,接受 H0 结论:消费者对 3 个新产品的态度没有改变。 &6.3 独立性测验 独立性测验(independence test)是测验两个变数之间是相互独立还是彼此 相关的统计方法,是次数资料的一种相关研究。 X2 独立性其步骤和方法是: H0:两个变数相互独立,HA:两个变数彼此相关。 将资料按两向分组排列成 r 行、c 列的相依表(表 5.3)。 X2 基本公式或变形公式计算值 按自由度 df=(r-1)( c-1)查表进行 x 2 测验。 写统计结论