章 第八章复因子试验方差分析 课时 4 &8.1复因子试验概述 &8.2二因素随机区组设计的结果分析 &8.3三因素随机区组设计的结果分析&8.4二因素裂区设计的结果分析 &8.5正交试验统计分析 教学 通过讲授,使学生了解复因子试验的必要性和优越性,掌握完全随机设计、 目的 随机区组设计、正交设计试验的方差分析,了解裂区试验资料的分析方法, 教学 重点 重点两因子(完全随机设计、随机区组设计和正交设计)试验的分析方法 教学 裂区试验的分析法、正交试验资料的分析。 难点 相关素材(参考资料、指导学生阅读材料等): 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008, 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9.《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10.《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002, 11.《试验设计与分析》,袁志发主编,高等教育出版社,2000
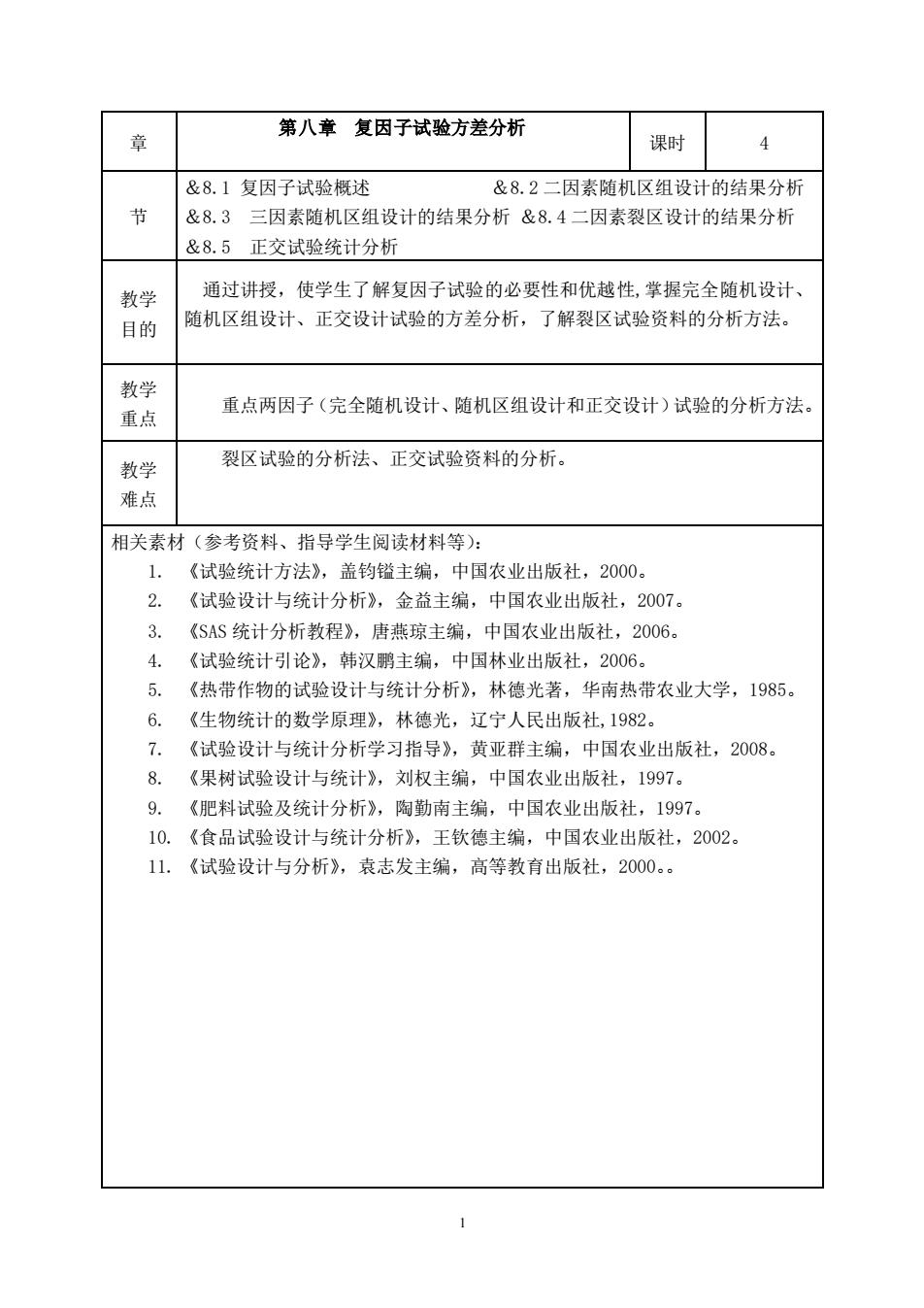
1 章 第八章 复因子试验方差分析 课时 4 节 &8.1 复因子试验概述 &8.2 二因素随机区组设计的结果分析 &8.3 三因素随机区组设计的结果分析 &8.4 二因素裂区设计的结果分析 &8.5 正交试验统计分析 教学 目的 通过讲授,使学生了解复因子试验的必要性和优越性,掌握完全随机设计、 随机区组设计、正交设计试验的方差分析,了解裂区试验资料的分析方法。 教学 重点 重点两因子(完全随机设计、随机区组设计和正交设计)试验的分析方法。 教学 难点 裂区试验的分析法、正交试验资料的分析。 相关素材(参考资料、指导学生阅读材料等): 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11. 《试验设计与分析》,袁志发主编,高等教育出版社,2000
教师授课思路、设问及讲解要点 “、引言 科研试验往往进行的是复因子试验,不仅要分析各因子水平间的比较、还分析 因子间的互作,处理组合效应的比较,即综合效果。本章将学习常用于复因子试验 设计资料的方差分析法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &8.1复因子试验概述 一、复因子试验的必要性 不仅能解决各因子水平间的比较问题,且能分析因子间的互作问题。 与同条件下的单因子试验精确度高 二、单、复因子试验方差分析不同点 1.必须将处理组合的SS和DF进一步分解为各个因子及其各项交互作用的SS 和D吓,从而进行因子主效应及交互作用效应的F测验。 2.要用二项表来计算各因子及各项交互作用的平方和 教 例如:2×4复因子试验,试作自由度分析。 (1)采用完全随机排列设计,重复3次 学 (2)采用随机区组设计,重复3次 (3)采用丁方设计 过 课堂练习: 2×3×4复因子试验,采用随机区组设计,重复3次,试作自由度分析。 &82二因子随机区组设计的结果分析 、 二因子随机区组试验的线性模型和期望均方 设有A、B两个试验因素,A因素有a个水平,B因素有b个水平,采用随机 区组设计,重复r次。共有b个水平组合,每一个水平组合有r个观察值。则该试 验共有rab个观察值。 变异来源DF SS MS 区组 r-1 MS. 处理组合 ab-1 SS, ΣT2-c MS A a-1 5S,= ∑i-c MSA b-1 s5=2-c MSB AXB (a-1b-1) SS4B =SS,-SS-SS8 MSA×B SS。=SS,-SS.-SS, 误差 (-lab-1) SS,=∑x2M-C MSe 总变异 rab-1
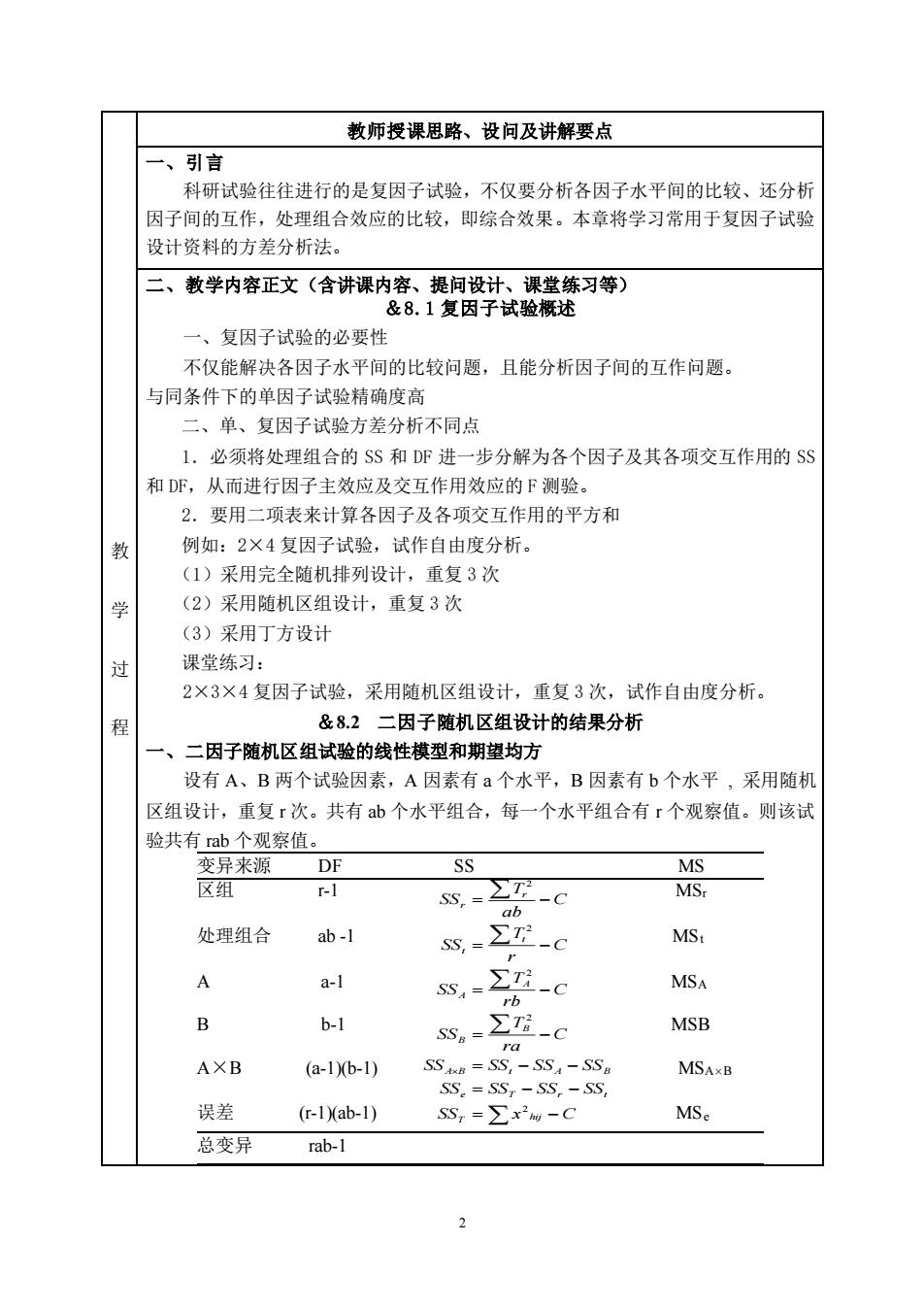
2 教 学 过 程 教师授课思路、设问及讲解要点 一、引言 科研试验往往进行的是复因子试验,不仅要分析各因子水平间的比较、还分析 因子间的互作,处理组合效应的比较,即综合效果。本章将学习常用于复因子试验 设计资料的方差分析法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &8.1 复因子试验概述 一、复因子试验的必要性 不仅能解决各因子水平间的比较问题,且能分析因子间的互作问题。 与同条件下的单因子试验精确度高 二、单、复因子试验方差分析不同点 1.必须将处理组合的 SS 和 DF 进一步分解为各个因子及其各项交互作用的 SS 和 DF,从而进行因子主效应及交互作用效应的 F 测验。 2.要用二项表来计算各因子及各项交互作用的平方和 例如:2×4 复因子试验,试作自由度分析。 (1)采用完全随机排列设计,重复 3 次 (2)采用随机区组设计,重复 3 次 (3)采用丁方设计 课堂练习: 2×3×4 复因子试验,采用随机区组设计,重复 3 次,试作自由度分析。 &8.2 二因子随机区组设计的结果分析 一、二因子随机区组试验的线性模型和期望均方 设有 A、B 两个试验因素,A 因素有 a 个水平,B 因素有 b 个水平 , 采用随机 区组设计,重复 r 次。共有 ab 个水平组合,每一个水平组合有 r 个观察值。则该试 验共有 rab 个观察值。 变异来源 DF SS MS 区组 r-1 MSr 处理组合 ab -1 MSt A a-1 MSA B b-1 MSB A×B (a-1)(b-1) MSA×B 误差 (r-1)(ab-1) MSe 总变异 rab-1 SS x C SS SS SS SS SS SS SS SS C raT SS C rbT SS C rT SS C abT SS hij T e T r t A B t A B B B A A t t r r = − = − − = − − = − = − = − = − 2 2 2 2 2
二因素随机区组的期望均方 变异 期望均方 来源 固定模型 随机模型 区组 o 2e+rb x2A B o 2+rak 2B a 2e+r o 2(AxB)+ra o 2B AXB a2e+rK 2(AxB) 02+r02A×B 误差 02。 02。 对于多因素试验而言,效应模型的不同将导致F测验的方法不同。 对固定模型来说,各变异项的均方除误差均方即构成相应的F测验。 H。:x2=0H。:x=0H。:x6=0,H。:x2B=0 MS技项 MS 但对随机模型来说,区组变异和互作变异用误差均方进行F测验:而A、B的 变异则应用互作项的均方进行F测验。 二因素随机区组与单因素随机区组的差别:二因素试验的处理项可以再分解为 教 A因素水平间、B因素水平间和AB互作三部分: SSt SSA+SSB+SSAxB (ab-1(a-1+b-1(a-1b-1) 其中,SS:为处理平方和:SSAxB为互作项平方和;SSA为A因素平方和;SSE 过 为B因素平方和。 二、二因素随机区组试验结果的分析实例 程 [例9.1]橡胶树品系A与栽培密度B试验,采用随机区组设计重复4次,测得 小区年干胶产量如下表,试作方差分析。 处理组合 A2 区组和 区组 B2 B3 BI B3 区组1 56 60 66 65 60 53 360 区组2 45 50 57 61 58 324 区组3 3 45 50 60 56 302 区组4 46 48 50 63 60 55 322 处理总和 190203223249 234209 T=1308 解 第一步:资料整理计算娇正数及各种平方和 Cs 13082 bn2x3x4=7186
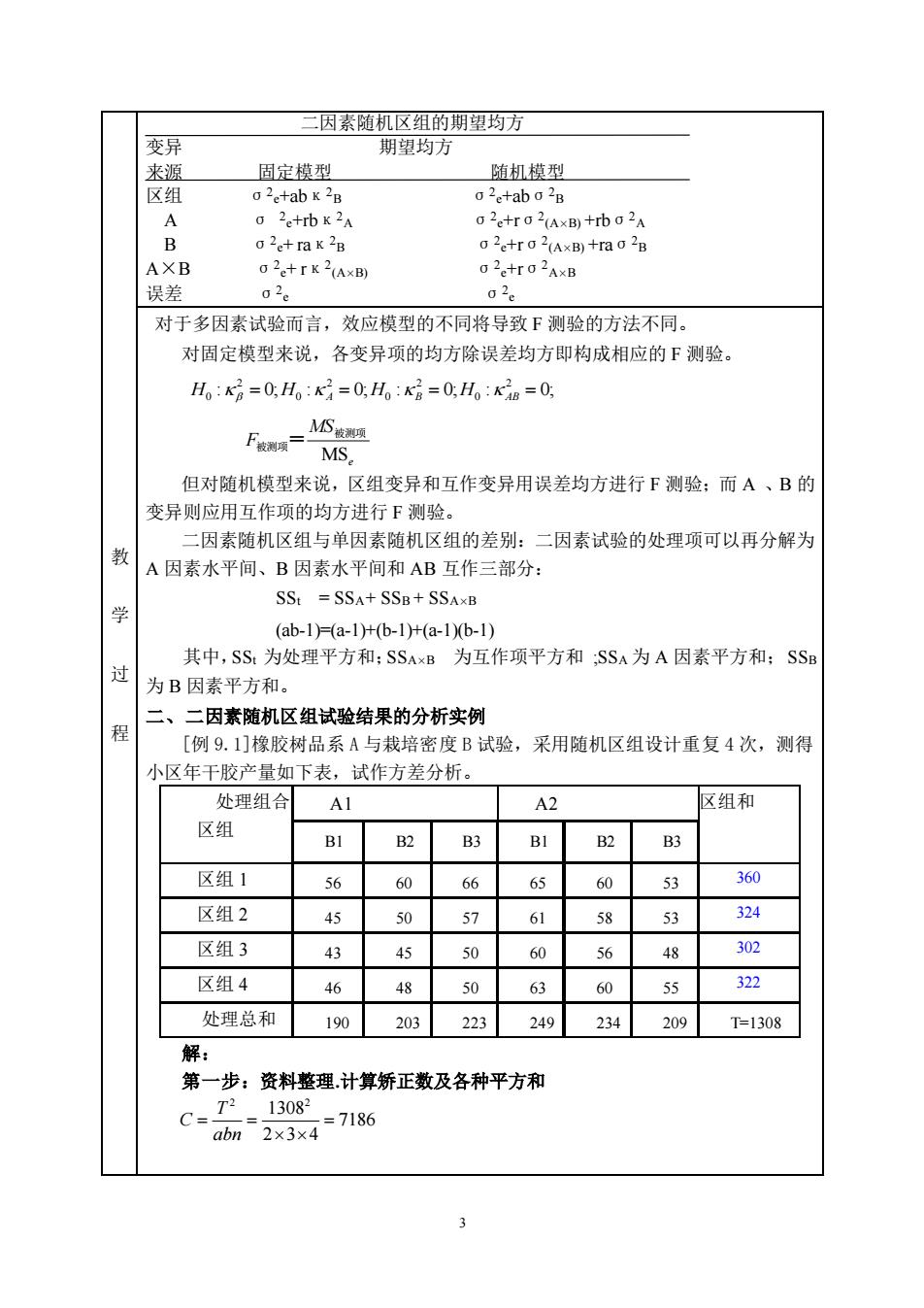
3 教 学 过 程 二因素随机区组的期望均方 变异 期望均方 来源 固定模型 随机模型 区组 σ2 e+abκ2 B σ2 e+abσ2 B A σ 2 e+rbκ2 A σ2 e+rσ2 (A×B) +rbσ2 A B σ2 e+ raκ2 B σ2 e+rσ2 (A×B) +raσ2 B A×B σ2 e+ rκ2 (A×B) σ2 e+rσ2 A×B 误差 σ2 e σ2 e 对于多因素试验而言,效应模型的不同将导致 F 测验的方法不同。 对固定模型来说,各变异项的均方除误差均方即构成相应的 F 测验。 e MS F MS 被测项 被测项 = 但对随机模型来说,区组变异和互作变异用误差均方进行 F 测验;而 A 、B 的 变异则应用互作项的均方进行 F 测验。 二因素随机区组与单因素随机区组的差别:二因素试验的处理项可以再分解为 A 因素水平间、B 因素水平间和 AB 互作三部分: SSt = SSA + SSB + SSA×B (ab-1)=(a-1)+(b-1)+(a-1)(b-1) 其中,SSt 为处理平方和;SSA×B 为互作项平方和 ;SSA 为 A 因素平方和;SSB 为 B 因素平方和。 二、二因素随机区组试验结果的分析实例 [例 9.1]橡胶树品系 A 与栽培密度 B 试验,采用随机区组设计重复 4 次,测得 小区年干胶产量如下表,试作方差分析。 处理组合 区组 A1 A2 区组和 B1 B2 B3 B1 B2 B3 区组 1 56 60 66 65 60 53 360 区组 2 45 50 57 61 58 53 324 区组 3 43 45 50 60 56 48 302 区组 4 46 48 50 63 60 55 322 处理总和 190 203 223 249 234 209 T=1308 解: 第一步:资料整理.计算矫正数及各种平方和 7186 2 3 4 1308 2 2 = = = abn T C : 0; : 0; : 0; : 0; 2 0 2 0 2 0 2 H0 = H A = H B = H AB =
SS。=∑Σx2-C=562+602++552-C=1036 5=7g-C=360+324++32-C=2913 2×3 %=27-C-190+203+ .+2092 -c=583 SS =SSg-SSs-SS=161.67 为了进一步分析处理间引起的变异原因,列出二向表, 以方便计算因子交互作用平方和。 BBI B2 B3 A和 A 190203 223 616 A2249234 209692 B和439437 4321308 学 ,=7 -c=6162+692 bn 3×4 -c=240.67 过 -c=439+4372+432 -c=325 an 2×4 55B=SS处n一S3A-5SB=339.08 第二步:列方差分析表并进行下测验 变异来源 自由度 平方和 均方 F值 区组 3 291.33 97.11 9.01 处理组合 583.00 116.60 10.82 品系A 240.67 240.67 22.33 施肥B 2 3.25 1.63 <1 交互AB 2 339.08 169.54 15.73 机误 161.67 10.78 总变异 1036.00 F测验结论: 7 第三步:多重比较(Duncan测验)(a=5%) 1.A多因子水平间(不用)
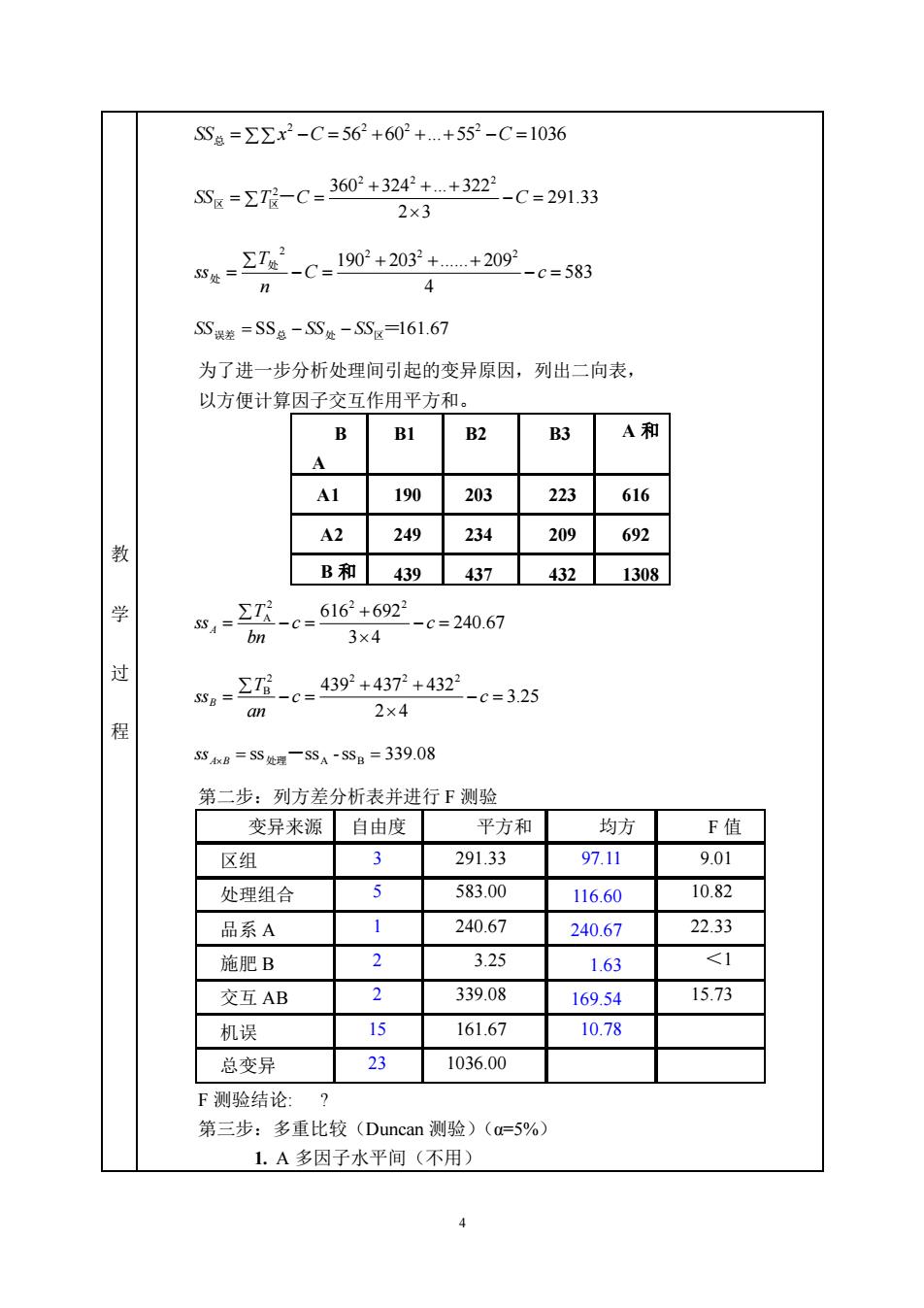
4 教 学 过 程 = − = 56 +60 +.+55 − =1036 2 2 2 2 SS总 x C C 291.33 2 3 360 324 . 322 2 2 2 2 − = + + + SS区 = T区-C = C 583 4 190 203 . 209 2 2 2 2 − = + + + − = = C c n T ss 处 处 SS误差 = SS总 − SS处 − SS区 =161.67 为了进一步分析处理间引起的变异原因,列出二向表, 以方便计算因子交互作用平方和。 B A B1 B2 B3 A 和 A1 190 203 223 616 A2 249 234 209 692 B 和 439 437 432 1308 240.67 3 4 616 692 2 2 2 A − = + − = = c c bn T ssA 3.25 2 4 439 437 432 2 2 2 2 B − = + + − = = c c an T ssB ssAB = ss处理-ssA -ssB = 339.08 第二步:列方差分析表并进行 F 测验 变异来源 自由度 平方和 均方 F 值 区组 3 291.33 97.11 9.01 处理组合 5 583.00 116.60 10.82 品系 A 1 240.67 240.67 22.33 施肥 B 2 3.25 1.63 <1 交互 AB 2 339.08 169.54 15.73 机误 15 161.67 10.78 总变异 23 1036.00 F 测验结论: ? 第三步:多重比较(Duncan 测验)(α=5%) 1. A 多因子水平间(不用)
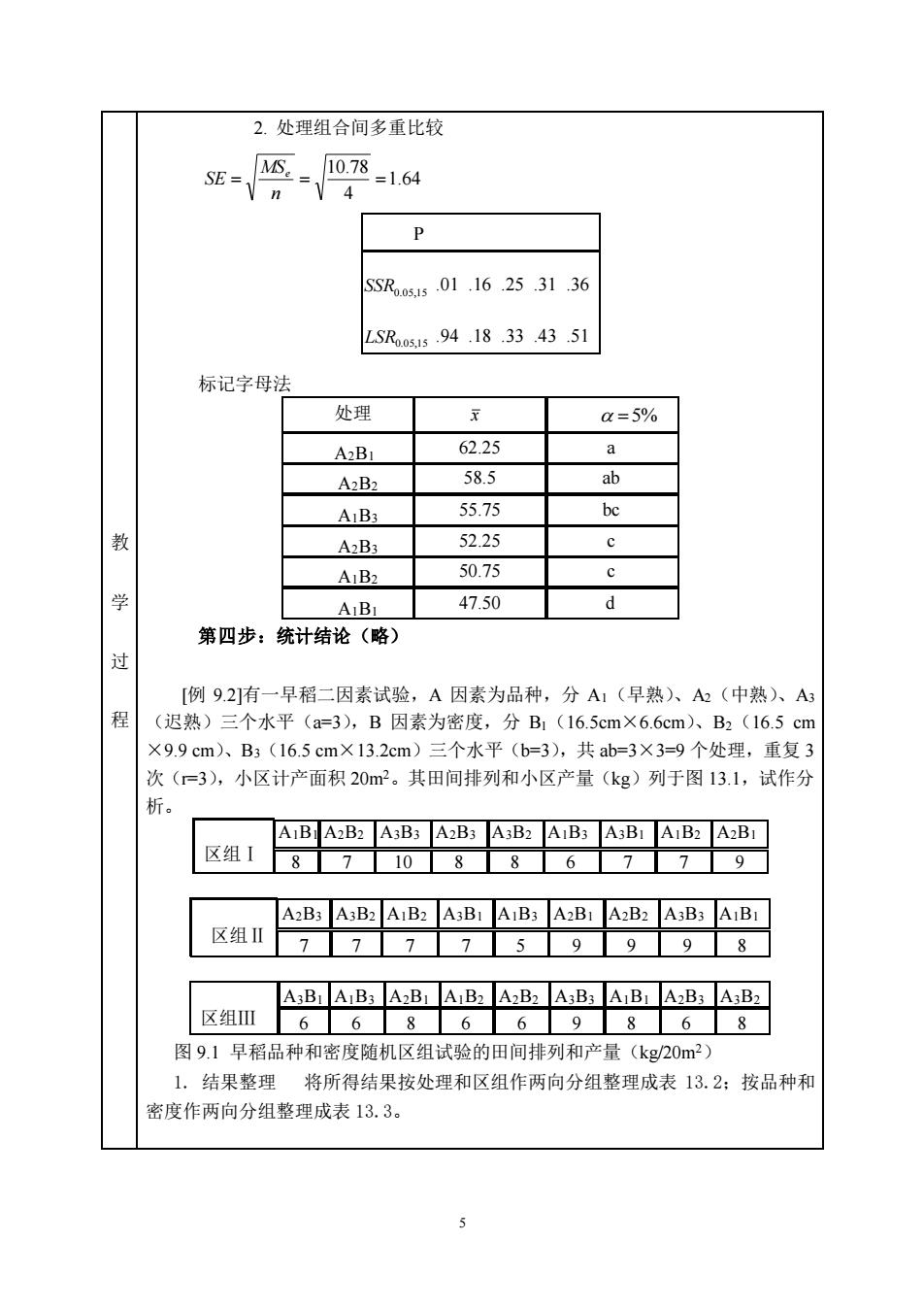
2.处理组合间多重比较 s.078-1.64 SE-V4 p SSRs501.16253136 LSR5594.18.3343.51 标记字母法 处理 a=5% A2BI 62.25 a A2B2 58.5 ab AB3 55.75 bc 教 A2B3 52.25 c AB2 50.75 c AiBI 47.50 d 第四步:统计结论(略) 过 [例9.2]有一早稻二因素试验,A因素为品种,分A1(早熟)入、A(中熟)、A3 程(迟熟)三个水平(a=3),B因素为密度,分B1(16.5cm×6.6cm)、B2(16.5cm ×9.9cm)、B;(16.5cm×13.2cm)三个水平(b=3),共ab=3×3=9个处理,重复3 次(=3),小区计产面积20m2。其田间排列和小区产量(kg)列于图13.1,试作分 析 AiBA2B2 A3B3 A2B3 A3B2 AiB3 A3BIAiB2 A2BI 区组18710886779 A2B3 A3B2A1B2 A3B1AIB3 A2BI A2B2 A3B3 A1BI 区组"777759998□ A3B:AiB:A2B:A:B2 A2B2 A:B:AuB:A2B:A:B2 区细m663669868 图9.1早稻品种和密度随机区组试验的田间排列和产量(kg20m2) 1.结果整理将所得结果按处理和区组作两向分组整理成表13.2:按品种和 密度作两向分组整理成表13.3
5 教 学 过 程 2. 处理组合间多重比较 1.64 4 10.78 = = = n MS SE e P 2 3 4 5 6 SSR0.05,15 3 .01 3 .16 3 .25 3 .31 3 .36 LSR0.05,15 4 .94 5 .18 5 .33 5 .43 5 .51 标记字母法 处理 x = 5% A2B1 62.25 a A2B2 58.5 ab A1B3 55.75 bc A2B3 52.25 c A1B2 50.75 c A1B1 47.50 d 第四步:统计结论(略) [例 9.2]有一早稻二因素试验,A 因素为品种,分 A1(早熟)、A2(中熟)、A3 (迟熟)三个水平(a=3),B 因素为密度,分 B1(16.5cm×6.6cm)、B2(16.5 cm ×9.9 cm)、B3(16.5 cm×13.2cm)三个水平(b=3),共 ab=3×3=9 个处理,重复 3 次(r=3),小区计产面积 20m2。其田间排列和小区产量(kg)列于图 13.1,试作分 析。 区组Ⅰ A1B1 A2B2 A3B3 A2B3 A3B2 A1B3 A3B1 A1B2 A2B1 8 7 10 8 8 6 7 7 9 区组Ⅱ A2B3 A3B2 A1B2 A3B1 A1B3 A2B1 A2B2 A3B3 A1B1 7 7 7 7 5 9 9 9 8 区组Ⅲ A3B1 A1B3 A2B1 A1B2 A2B2 A3B3 A1B1 A2B3 A3B2 6 6 8 6 6 9 8 6 8 图 9.1 早稻品种和密度随机区组试验的田间排列和产量(kg/20m2) 1. 结果整理 将所得结果按处理和区组作两向分组整理成表 13.2;按品种和 密度作两向分组整理成表 13.3