要 第七章单因子试验方差分析 课时 10 &7.1方差分析的必要性与作用&7.2方差分析的条件与数据转换 &7.3方差分析及基本原理 &7.4方差分析的类型与分析步骤 &7.5完全随机设计 &7.6随机区组设计 &7.7拉丁方设计 教学 (1)了解方差分析的基本原理和步骤:(2)掌握统计学两类错误:(3)了 目的 解方差分析的基本假定和数据转换方法。(4)学握完全随机设计、随机区 组设计、拉丁方设计等单因子试验资料的方差分析。 1.方差分析的基本原理和步骤 教学 2. 统计学两类错误 3.方差分析的条件和数据转换方法。 重点 4.完全随机设计的方差分析与随机区组设计的方差分析。 1.方差分析的基本原理 2.常用的数据代换的适用范围理解 3.各种试验资料分析方法的判断及分析时异同。 突破方法: 教学 举例与多媒体图形展示讲解。先温习各种设计的特点,使从试验设计 难点 过程中掌握各种设计误差的不同。重点讲透完全随机设计的总平方和的分 解,区组设计只多了项区组平方和等,学生很快就会自己写出拉丁方设计 资料的分析公式。此外,通过再做课堂练习,学生掌握了再往下讲。效果 较好。 相关素材(参考资料、指导学生阅读材料等): 1. 《试验统计方法》,盖钧镫主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008, 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9.《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10.《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002 11.《试验设计与分析》,袁志发主编,高等教育出版社,2000
1 章 第七章 单因子试验方差分析 课时 10 节 &7.1 方差分析的必要性与作用 &7.2 方差分析的条件与数据转换 &7.3 方差分析及基本原理 &7.4 方差分析的类型与分析步骤 &7.5 完全随机设计 &7.6 随机区组设计 &7.7 拉丁方设计 教学 目的 (1)了解方差分析的基本原理和步骤;(2)掌握统计学两类错误;(3)了 解方差分析的基本假定和数据转换方法。(4)掌握完全随机设计、随机区 组设计、拉丁方设计等单因子试验资料的方差分析。 教学 重点 1. 方差分析的基本原理和步骤 2. 统计学两类错误 3. 方差分析的条件和数据转换方法。 4. 完全随机设计的方差分析与随机区组设计的方差分析。 教学 难点 1. 方差分析的基本原理 2. 常用的数据代换的适用范围理解 3. 各种试验资料分析方法的判断及分析时异同。 突破方法: 举例与多媒体图形展示讲解。先温习各种设计的特点,使从试验设计 过程中掌握各种设计误差的不同。重点讲透完全随机设计的总平方和的分 解,区组设计只多了项区组平方和等,学生很快就会自己写出拉丁方设计 资料的分析公式。此外,通过再做课堂练习,学生掌握了再往下讲。效果 较好。 相关素材(参考资料、指导学生阅读材料等): 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11. 《试验设计与分析》,袁志发主编,高等教育出版社,2000

教师授课思路、设问及讲解要点 一、引言 前面学习的均数差异显著性测验,用于比较两个试验处理的优劣,而科研实 践往往需进行多个处理平均数间差异显著性测验。例如比较5种药剂的抑菌效果 的差异显著性测验。4个菌种在3种不同培养基的生长效果比较试验。这就要用 本章将学的方差分析法,它是解决多个处理效果差异显著性测验的统计方法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &7.1方差分析的必要性与作用 一、方差分析的必要性 前面学习了两个样本平均数的假设测验,该法只适用于比较两个试验处理 的优劣。用于多个平均数间差异显著性测验,就会表现出如下一些问题: 1.多个处理用t测验计算麻烦 前面讲过的t测验,卡平方测验多数只限于2个处理进行比较,而对多个处 教理进行比较,就麻烦,又不能利用资料的全部信息,精确度也不高。例如:有10 个样本,就要测验:u=2,u=u,共C=45个假设,很麻烦。 学 2.推断的可靠性降低,犯α错误的概率增大 两个样本平均数比较采用t测验,a=0.05时犯第一类错误的概率为0.05 过 推断的可靠性为1-a=0.95。 若对5个处理采用t测验进行比较,ā=0.05,需进行10次两两比较,每次 比较的可靠性为1-α=0.95,要求10次都正确的概率为(1-a)10 0.9510=0.5987,因此推断的可靠性由0.95降到0.5987,犯第一类错误的概率则由 0.05上升到(1-0.5987)=0.4013. 3.误差估计的精确性和检验的灵敏性降低 对同一试验的多个处理进行比较时,应该有一个统一的试验误差的估计值。 采用t测验法,每次只能利用两组观察值估计试验误差,与利用全部观察值估计 的试验误差相比,精确性低,误差的自由度也低,从而使检验的灵敏度也降低, 容易掩盖差异的显著性,增大犯第二类错误的可能。 譬如,有5个处理,每个处理重复6次,共有观察值30个,若进行t测验每 次只利用12个观察值,误差的自由度为2(6-1)=10,若利用30个观察值估计 试验误差,误差自由度为5(6-1)=25。自由度越小,标准差越大,灵敏度低: 自由度越大,标准差越小,灵敏度高。 因此对多个处理平均数进行差异显著性测验,不宜采用t测验,而需采用 种新的统计方法一一方差分析法
2 教 学 过 程 教师授课思路、设问及讲解要点 一、引言 前面学习的均数差异显著性测验,用于比较两个试验处理的优劣,而科研实 践往往需进行多个处理平均数间差异显著性测验。例如比较 5 种药剂的抑菌效果 的差异显著性测验。4 个菌种在 3 种不同培养基的生长效果比较试验。这就要用 本章将学的方差分析法,它是解决多个处理效果差异显著性测验的统计方法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &7.1 方差分析的必要性与作用 一、方差分析的必要性 前面学习了两个样本平均数的假设测验,该法只适用于比较两个试验处理 的优劣。用于多个平均数间差异显著性测验,就会表现出如下一些问题: 1.多个处理用 t 测验计算麻烦 前面讲过的 t 测验,卡平方测验多数只限于2个处理进行比较, 而对多个处 理进行比较,就麻烦,又不能利用资料的全部信息,精确度也不高。例如:有 10 个样本,就要测验:u1=u2, u1=u3 .,共 2 C10=45 个假设,很麻烦。 2.推断的可靠性降低 ,犯α错误的概率增大 两个样本平均数比较采用 t 测验,α=0.05 时犯第一类错误的概率为 0.05, 推断的可靠性为 1-α=0.95。 若对 5 个处理采用 t 测验进行比较,α=0.05, 需进行 10 次两两比较,每次 比 较 的 可 靠 性 为 1-α=0.95 , 要 求 10 次 都 正 确 的 概 率 为 (1-α)10 = 0.9510=0.5987,因此推断的可靠性由 0.95 降到 0.5987,犯第一类错误的概率则由 0.05 上升到(1-0.5987)=0.4013. 3.误差估计的精确性和检验的灵敏性降低 对同一试验的多个处理进行比较时,应该有一个统一的试验误差的估计值。 采用 t 测验法,每次只能利用两组观察值估计试验误差,与利用全部观察值估计 的试验误差相比,精确性低,误差的自由度也低,从而使检验的灵敏度也降低, 容易掩盖差异的显著性,增大犯第二类错误的可能。 譬如,有 5 个处理,每个处理重复 6 次,共有观察值 30 个,若进行 t 测验每 次只利用 12 个观察值,误差的自由度为 2(6-1)=10,若利用 30 个观察值估计 试验误差,误差自由度为 5(6-1)=25。自由度越小,标准差越大,灵敏度低; 自由度越大,标准差越小,灵敏度高。 因此对多个处理平均数进行差异显著性测验,不宜采用 t 测验,而需采用一 种新的统计方法——方差分析法

&7.2方差分析的条件与数据转换 、方差分析的基本假定(条件)p143 1.正态性:指所有试验误差都是随机的、彼此独立的,且服从正态分布 N(0,σ2),一般量测性资料都满足正态性 2.可加性(独立性):处理效应与环境效应等应该具有可加性。各样本间相 互独立的。 3.方差齐性(同质性):所有处理的误差方差都是同质的。可用卡平方测验 窥测。 对于测量性资料,一般都满足这四条,尽可放心使用方差分析,计数性资料 往往不能满足4点要求,常要进行统计代换,用代换后的数据作方差分析。 二.计数性资料的统计代换 (一)、平方根代换 1.公式:x=√ x=x+1 (x中含0) 教 2适用范围:各组方差与其平均数有某种比例关系的资料。 服从潘松分布的资料,这类资料一般不用百分率来表示,而用计数表示, 学 如每小区的虫数、杂草数、放射性物质在单位时间内的放射次数等,调查总数很 大,但昆虫出现头数极少或某性状出现的次数很少,通常)50。 3,方法:查平方根表或计算器 过 (二)、对数代换 1.公式:x’=1gx(不含0) x’=1g(x+1)(有含0) 程 2,适用范围:数据表现的效应为非可加性,而成倍加性或可乘性,同时平 均数与其极差或s成比例或艰CV接近一常数时。 服从核心分布或负二项分布(嵌纹分布)的资料 核心分布:呈一小群一小群的相对集中的分布,而群与群之间的位置又是随 机的。 嵌纹分布:又负二项分布,即是边缘变化的分布,有的地方很多,而有的地 方又很少,其间断过渡的。 火 资料特点各处理的标准差、极差与其平均数成比例的趋势或变异系数 接近一个常数时。如倍数表现为倍加性或可乘性,对数代换比平方根 更有效。 (三)、反正弦代换 1.公式:用角度表示:x=sn1其中:x为百分率x'为角度值 用弧度表示:0如 2.适用范围:资料系成数或百分数
3 教 学 过 程 &7.2 方差分析的条件与数据转换 一、方差分析的基本假定(条件)p143 1.正态性:指所有试验误差都是随机的、彼此独立的,且服从正态分布 (0, ) 2 N ,一般量测性资料都满足正态性。 2.可加性(独立性):处理效应与环境效应等应该具有可加性。各样本间相 互独立的。 3.方差齐性(同质性):所有处理的误差方差都是同质的。可用卡平方测验 窥测。 对于测量性资料,一般都满足这四条,尽可放心使用方差分析,计数性资料, 往往不能满足4点要求,常要进行统计代换,用代换后的数据作方差分析。 二.计数性资料的统计代换 (一)、 平方根代换 1.公式: x = x x = x +1 (x中含 0) 2.适用范围:各组方差与其平均数有某种比例关系的资料。 服从潘松分布的资料,这类资料一般不用百分率来表示,而用计数表示, 如每小区的虫数、杂草数、放射性物质在单位时间内的放射次数等,调查总数很 大,但昆虫出现头数极少或某性状出现的次数很少,通常 n〉50。 3.方法:查平方根表或计算器 (二)、对数代换 1.公式:x’=lgx(不含 0) x’=lg(x+1)(有含 0) 2.适用范围:数据表现的效应为非可加性,而成倍加性或可乘性,同时平 均数与其极差或 s 成比例或艰 CV 接近一常数时。 服从核心分布或负二项分布(嵌纹分布)的资料。 核心分布:呈一小群一小群的相对集中的分布,而群与群之间的位置又是随 机的。 嵌纹分布:又负二项分布,即是边缘变化的分布,有的地方很多,而有的地 方又很少,其间断过渡的。 * 资料特点各处理的标准差、极差与其平均数成比例的趋势或变异系数 接近一个常数时。如倍数表现为倍加性或可乘性,对数代换比平方根 更有效。 (三)、反正弦代换 1.公式:用角度表示: x x 1 sin − = 其中:x 为百分率 x’为角度值 用弧度表示: x x 1 sin 180 − = 2.适用范围:资料系成数或百分数
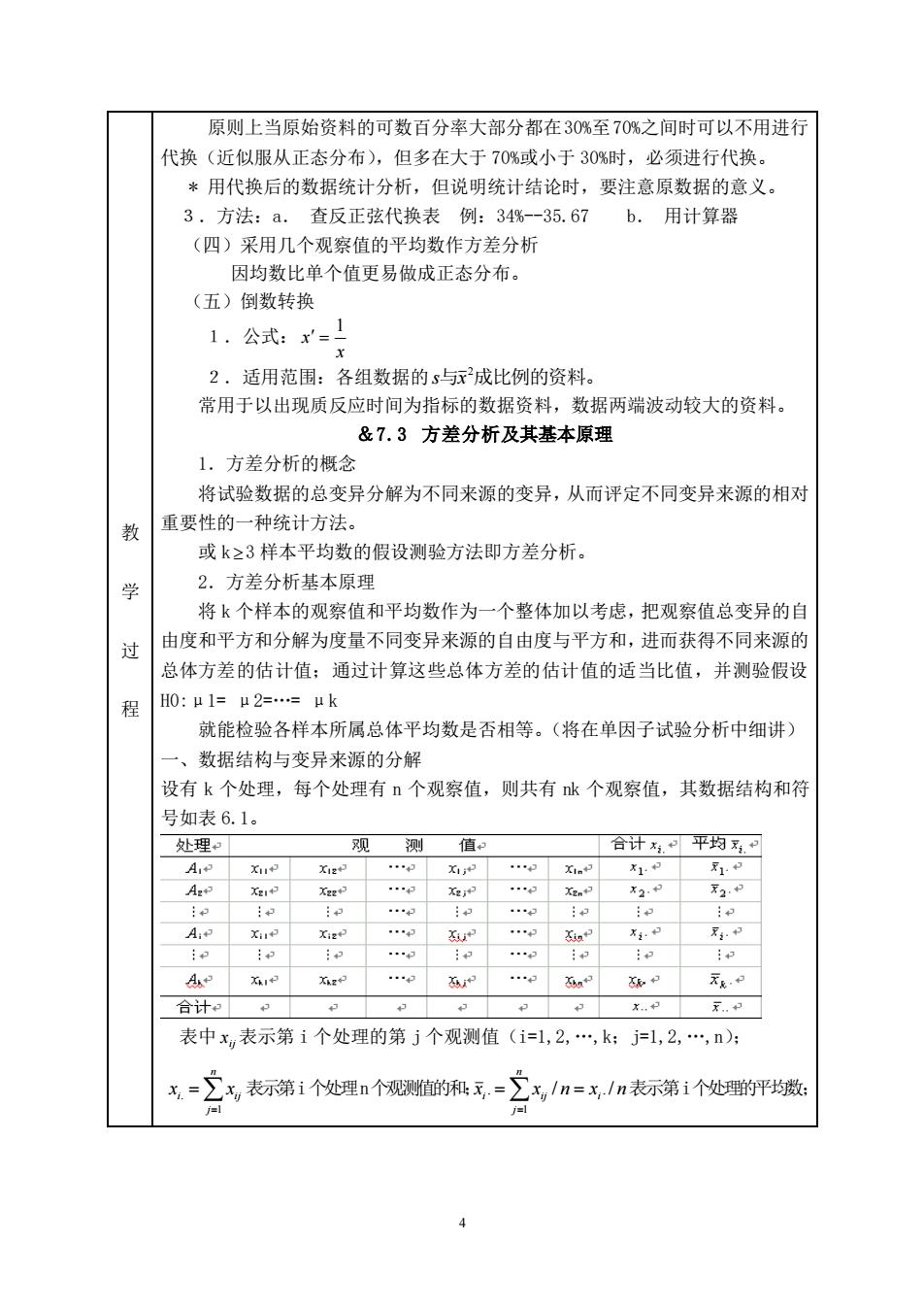
原则上当原始资料的可数百分率大部分都在30%至70%之间时可以不用进行 代换(近似服从正态分布),但多在大于70%或小于30%时,必须进行代换。 *用代换后的数据统计分析,但说明统计结论时,要注意原数据的意义。 3.方法:a.查反正弦代换表例:34%-35.67 b.用计算器 (四)采用几个观察值的平均数作方差分析 因均数比单个值更易做成正态分布, (五)倒数转换 1,公式:x=I 2.适用范围:各组数据的s与F成比例的资料。 常用于以出现质反应时间为指标的数据资料,数据两端波动较大的资料, &7.3方差分析及其基本原理 1.方差分析的概念 将试验数据的总变异分解为不同来源的变异,从而评定不同变异来源的相为 教 重要性的一种统计方法。 或k≥3样本平均数的假设测验方法即方差分析。 2.方差分析基本原理 将k个样本的观察值和平均数作为一个整体加以考虑,把观察值总变异的自 过 由度和平方和分解为度量不同变异来源的自由度与平方和,进而获得不同来源的 总体方差的估计值:通过计算这些总体方差的估计值的适当比值,并测验假设 程 H0:μ1=μ2==μk 就能检验各样本所属总体平均数是否相等。(将在单因子试验分析中细讲) ·、数据结构与变异来源的分解 设有k个处理,每个处理有n个观察值,则共有k个观察值,其数据结构和符 号如表6.1。 处理3 合计,平均.⊙ 1 x2.2. A: x4. Xz? 合计和中 . 表中x表示第i个处理的第j个观测值(i=l,2,.,k:jl,2,.,n): x=立x,表示第i个处理n个规测值的秘=立,1m=X,1n衣示第1个处的平药藏
4 教 学 过 程 原则上当原始资料的可数百分率大部分都在30%至70%之间时可以不用进行 代换(近似服从正态分布),但多在大于 70%或小于 30%时,必须进行代换。 * 用代换后的数据统计分析,但说明统计结论时,要注意原数据的意义。 3.方法:a. 查反正弦代换表 例:34%-35.67 b. 用计算器 (四)采用几个观察值的平均数作方差分析 因均数比单个值更易做成正态分布。 (五)倒数转换 1.公式: x x 1 = 2.适用范围:各组数据的 s与x 2成比例的资料。 常用于以出现质反应时间为指标的数据资料,数据两端波动较大的资料。 &7.3 方差分析及其基本原理 1.方差分析的概念 将试验数据的总变异分解为不同来源的变异,从而评定不同变异来源的相对 重要性的一种统计方法。 或 k 3 样本平均数的假设测验方法即方差分析。 2.方差分析基本原理 将 k 个样本的观察值和平均数作为一个整体加以考虑,把观察值总变异的自 由度和平方和分解为度量不同变异来源的自由度与平方和,进而获得不同来源的 总体方差的估计值;通过计算这些总体方差的估计值的适当比值,并测验假设 H0:μ1= μ2=.= μk 就能检验各样本所属总体平均数是否相等。(将在单因子试验分析中细讲) 一、数据结构与变异来源的分解 设有 k 个处理,每个处理有 n 个观察值,则共有 nk 个观察值,其数据结构和符 号如表 6.1。 表中 ij x 表示第 i 个处理的第 j 个观测值(i=1,2,.,k;j=1,2,.,n); = = n j i ij x x 1 . 表示第i个处理n个观测值的和; x x n xi n n j i ij . / ./ 1 = = = 表示第i个处理的平均数;

女一身表示第个处理个观测值的和: 上一字护宫表标全都观测做的和 黑一空以=年加表示第1个处理的平均数 玉一空艺ax加表标全部观测值的总平约数, 处理间变异ti=(μi-μ) 处理内变异eij=(xijμi) x,=元+1,+e,样本符号 μ表示全试验观测值总体的平均数 由此可推知:k个观察值的总变异可分解为处理间的变异和处理内的变异两 部分。 二、自由度与平方和的分解 教 1、总平方和分解 由表7.1可以看出,k个观察值的变异构成了整个资料的总变异,总变异的 学 平方和即: s-X4-8-君 过 x,-=际-)+6,- 程 =2年-户+2民-X-)+(6-月 =吃属-广+2[属-),-月+22,- 其中2x,-)=0 所吃2-=空低-+224,- 总平方和=处理间平方和+处理内平方和 记为:SST=SSt+SSe 处理间平方和乃各处理的平均数的变异 馬=心低-驴区列- 处理内(误差)平方和乃各组的个观察值与其相应平均数的离差平方和,即 2k-矿=2号买
5 教 学 过 程 = = n j i ij x x 1 . 表示第 i 个处理 n 个观测值的和; = = = = = k i i k i n j ij x x x 1 1 1 . . 表示全部观测值的总和; x x n xi n n j i ij . / ./ 1 = = = 表示第 i 个处理的平均数 x x kn x kn k i n j ij . / ./ 1 1 = = = = 表示全部观测值的总平均数; 处理间变异τi=(μi- μ) 处理内变异εij=( xij- μi) ij i ij x = x + t + e 样本符号 μ表示全试验观测值总体的平均数 由此可推知: nk 个观察值的总变异可分解为处理间的变异和处理内的变异两 部分。 二、自由度与平方和的分解 1、总平方和分解 由表 7.1 可以看出,nk 个观察值的变异构成了整个资料的总变异,总变异的 平方和即: nk T ss x x x T ij ij 2 2 2 =( − ) = − = − + − − + − = − + − − + − − = − + − = = = = = = = = = = = k i n j i j i n j i j i k i k i i i k i n j i i i j i i j i k i n j k i n j i j i i j i n x x x x x x x x x x x x x x x x x x x x x x 1 1 2 1 1 1 2 1 1 2 2 1 1 1 1 2 2 ( . .) 2 [( . .) ( .)] ( .) ( . .) 2( . .)( .) ( .) ( .) ( . .) ( .) = − = n j ij i x x 1 其中 ( . ) 0 = = = = = − = − + − k i n j k i k i n j ij i ij i x x n x x x x 1 1 1 1 1 2 . 2 . . 2 . 所以 ( ) ( ) ( ) 总平方和=处理间平方和+处理内平方和 记为:SST = SSt+ SSe 处理间平方和乃各处理的平均数的变异, = − = − nk T T n ss n x x t i i 2 2 2 ( ) 1 ( ) 处理内(误差)平方和乃各组的 n 个观察值与其相应平均数的离差平方和,即 n T ss x x x i nk ij k n e ij i = − = − 2 1 2 2 1 1 ( )