
第8章时序逻辑电路 本章讨论了数字电路的另一类单元电路一一时序逻辑电路。首先介绍具有存 储记忆功能的单元电路触发器,它是构成各种计数器和寄存器等时序电路的单 元。然后介绍数字系统中常用的一些时序电路的组成和工作原理以及555定时器 的应用。 本章基本要求 了解时序逻辑电路的共同特点: 熟练掌握R-S、JK、D、T触发器的逻辑功能: 熟练掌握时序电路分析方法,基本的设计方法: 掌握计数器的分类及特点: 了解常用的时序逻辑电路的功能及应用: 了解555定时器的典型应用。 本章习题解析 aw.com 8一5在图8-6中,设每个触发器的初始状态为“0”,试画出在时钟脉冲CP作 用下Q的波形。 解: (a)图中: 超超 0=J@+K0”=0 (b)图中: O=Jo"+Ko"=0 " e (d) (c)图中: CP 0=J0"+KQ"=0m (d图中: 图8-6 Q1=D=0 cPTΠΠΠ (e)图中:Q=D=Q” (①图中:Q1=JQ”+KQ"=Q” 02 各触发器的波形图如下图8-7所示: 9☐ O 25 图8-7 8一6电路如图8-8所示,设初始状态为9=Q2=0,,试画出在CP作用下Q1、 Q2的波形
第 8 章 时序逻辑电路 本章讨论了数字电路的另一类单元电路——时序逻辑电路。首先介绍具有存 储记忆功能的单元电路触发器,它是构成各种计数器和寄存器等时序电路的单 元。然后介绍数字系统中常用的一些时序电路的组成和工作原理以及 555 定时器 的应用。 本章基本要求 了解时序逻辑电路的共同特点; 熟练掌握 R-S、J-K、D、T 触发器的逻辑功能; 熟练掌握时序电路分析方法,基本的设计方法; 掌握计数器的分类及特点; 了解常用的时序逻辑电路的功能及应用; 了解 555 定时器的典型应用。 本章习题解析 8-5 在图 8-6 中,设每个触发器的初始状态为“0”,试画出在时钟脉冲 CP 作 用下 Q 的波形。 解: (a) 图中: ___ ___ ___ 1 1 1 n n n n Q J Q K Q Q (b) 图中: 0 1 2 n n n Q JQ KQ (c) 图中: ___ ___ ____ 1 3 n n n n Q J Q K Q Q (d) 图中: 0 1 4 Q D n (e) 图中: n n Q D Q 1 5 (f) 图中: n n n n Q JQ KQ Q 1 6 各触发器的波形图如下图 8-7 所示: 8-6 电路如图 8-8 所示,设初始状态为 Q1 Q2 0 ,,试画出在 CP 作用下 Q1 、 Q2 的波形。 Q J K CP Q J K Q CP Q J K Q CP Q Q CP D Q Q CP D Q J K Q CP Q CP 图8--6 (a) (b) (c) (d) (e) (f) “1” “1” “1” “1” “0” “1” CP Q1 Q6 Q5 Q4 Q3 Q2 图 8-7

解:Q=JQ+Kg=QQ+Q·Q=Q"02 O2=D=Om 波形图如图8-9所示: cP冂Π冂几 0, 图8-9 CP 图8-8 8一7电路如图8-10所示,设初始状态为9=Q2=0,试画出在CP作用下Q,、 Q2的波形。 解:Q1=D=Q” 02"D:=0" 波形图如下图8-11所示: Q D. D. o,C 92 图8-10 图8-11 8一8图8-12所示为TTL维持阻塞D触发器,试分析其逻辑功能,列出真值表, 并说明图中①~④连线的作用。 (1) G 解: 工作原理分析: R。S接至基本RS触发器的输入端,分别是 (2) 清零和预置数端,低电平有效。当S。=R。=1时, CPO (3) 工作过程如下: 图8-12 ①CP=0时,触发器状态不变。此时Q=D, 2=D ②CP由0变1时触发器翻转,Q=D ③CP=1时输入信号被封馈,触发器保持,其中反馈线①使触发器维持在0 状态和阻止触发器为1状态称为置0维持线,置1阻塞线。 反馈线②使CP=0,Q,=D时,Q。=D 反馈线③使CP=1时,触发器维持1状态即置1维持线
解: n n n n n n n n n Q JQ1 KQ1 Q2 Q1 Q2 Q1 Q1 Q2 1 1 n n Q D Q1 1 2 波形图如图 8-9 所示: 8-7 电路如图 8-10 所示,设初始状态为 Q1 Q2 0 ,,试画出在 CP 作用下 Q1 、 Q2 的波形。 解: n n Q D1 Q1 1 1 n n Q D2 Q2 1 2 波形图如下图 8-11 所示: 8-8 图 8-12 所示为 TTL 维持阻塞 D 触发器,试分析其逻辑功能,列出真值表, 并说明图中①~④连线的作用。 解: 工作原理分析: RD S D 接至基本 RS 触发器的输入端,分别是 清零和预置数端,低电平有效。当 SD RD 1 时, 工作过程如下: ① CP 0 时,触发器状态不变。此时 Q5 D , Q6 D ② CP 由 0 变 1 时触发器翻转, Q D ③ CP 1 时输入信号被封馈,触发器保持,其中反馈线①使触发器维持在 0 状态和阻止触发器为 1 状态称为置 0 维持线,置 1 阻塞线。 反馈线②使 CP 0,Q5 D 时, Q6 D 反馈线③使 CP 1 时,触发器维持 1 状态即置 1 维持线。 图 8-9 CP Q2 Q1 图 8-8 J CPK Q Q CP D CP Q1 Q2 图 8-10 C CP Q2 D2 Q1 D1 C Q2 Q1 图 8-11 CP Q2 Q1 图 8-12 (1) & & & & & & CP D Q Q Q5 Q6 Q3 Q4 G1 G2 (2) (3) (4)
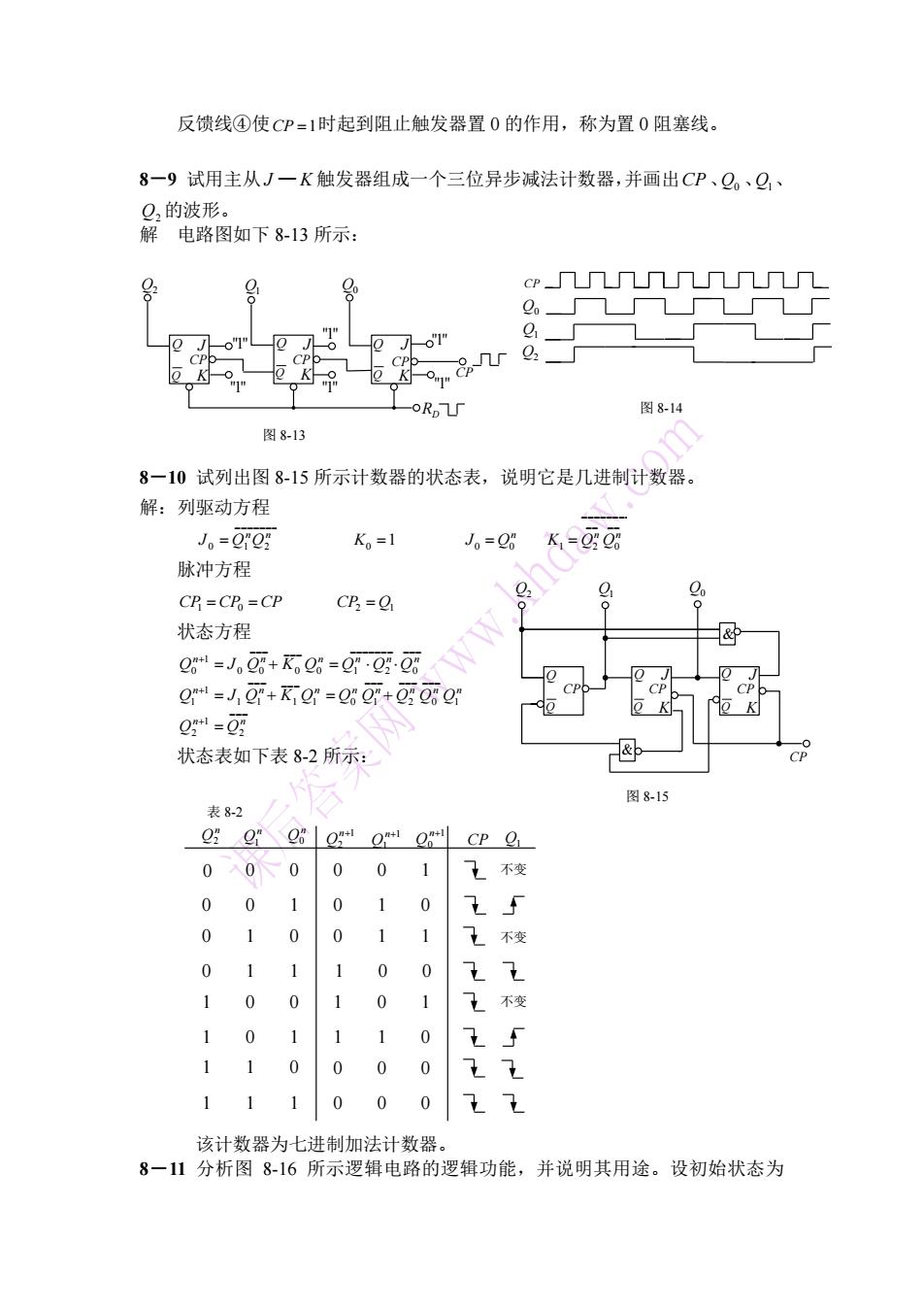
反馈线④使CP=1时起到阻止触发器置0的作用,称为置0阻塞线。 8一9试用主从J一K触发器组成一个三位异步减法计数器,并画出CP、Q。、Q、 Q2的波形。 解电路图如下8-13所示: cPΠ冂冂ΠΠΠΠ厂 P 92 图8-14 图8-13 8一10试列出图8-15所示计数器的状态表,说明它是几进制计数器。 解:列驱动方程 J=0^0 K。=1 J。=Q6 K=Q 脉冲方程 Qo CP=CPo=CP CP=C 状态方程 Q1=J0。+K06=g00 WW 0+=Jg+Ki0"=Q60+0 CP 01=0 状态表如下表8-2所示: CP 图8-15 表8-2 」Q0Q8Cp9 0 入00 0 0 7不变 0 0 1 0 1 0 0 1 0 0 1 1 不变 0 1 0 0 1 0 0 1 0 1 不变 1 0 1 0 飞 1 1 0 0 0 0 1 1 0 0 该计数器为七进制加法计数器。 8一11分析图8-16所示逻辑电路的逻辑功能,并说明其用途。设初始状态为
反馈线④使 CP 1 时起到阻止触发器置 0 的作用,称为置 0 阻塞线。 8-9 试用主从 J — K 触发器组成一个三位异步减法计数器,并画出 CP 、Q0 、Q1、 Q2 的波形。 解 电路图如下 8-13 所示: 8-10 试列出图 8-15 所示计数器的状态表,说明它是几进制计数器。 解:列驱动方程 _______ 0 1 2 n n J Q Q K0 1 n J 0 Q0 ________ __ 0 __ 1 2 n n K Q Q 脉冲方程 CP1 CP0 CP CP2 Q1 状态方程 ___ 0 _______ 0 1 2 ___ 0 ___ 0 0 1 0 n n n n n n Q J Q K Q Q Q Q n n n n n n n n Q J Q K Q Q Q Q Q Q1 ___ 0 ___ 2 ___ 1 0 1 ___ 1 ___ 1 1 1 1 ___ 2 1 2 n n Q Q 状态表如下表 8-2 所示: 该计数器为七进制加法计数器。 8-11 分析图 8-16 所示逻辑电路的逻辑功能,并说明其用途。设初始状态为 K J Q Q CP Q1 Q0 Q Q CP Q2 K J Q Q CP J K RD CP "1" "1" "1" "1" "1" "1" 图 8-13 CP Q1 Q2 Q0 图 8-14 K K J J Q Q Q Q Q Q CP CP CP Q2 Q1 Q0 & & CP 图 8-15 表 8-2 n Q2 n Q1 n Q0 1 2 n Q 1 1 n Q 1 0 n Q CP Q1 0 0 0 不变 不变 不变 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 1 1 0 1 1 0 0 0 0 1 1 1 0 0 0

“0000”,画出CP、Q。、Q、Q2、Q的波形。 图 0清零 计数脉冲 nnn 图8-16 解:列驱动方程 J0=K0=1 J=K1=06.0j J:=K:=Q".Q6.0j J3=05·g"·Q6·0 K3=20 w.khdaw.com 状态方程为 Q1=J+06=Q o"=Jo+o"=0of 0"+06.oo 0=J20+2g5=0,Qo+0"Q6.g05 QM=J0+Ko:=0:.0"00 o +0001 表8-3 9马9⊥C10Q1 状态转换表如下表83所示: 000 0 0 101 画出状态转换图可得该电路为一十进制 00 1 001 0 加法计数器,且能自启动。 0 0 1 0 1 1 00 1 1 0 00 0 01 0 0 0 10 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 1 1 10 1 1 0
“0000”,画出 CP 、Q0 、Q1、Q2 、Q3 的波形。 解:列驱动方程 J 0 K0 1 ___ 1 1 0 3 n n J K Q Q ___ 2 2 1 0 3 n n n J K Q Q Q ___ 3 2 1 0 3 n n n n J Q Q Q Q n K3 Q0 状态方程为 ___ 0 0 ___ 0 ___ 0 0 1 0 n n n n Q J Q K Q Q n n n n n n n n n Q J Q K Q Q Q Q Q Q Q1 _________ ___ 0 3 ___ 1 ___ 1 0 3 ___ 1 ___ 1 1 1 1 n n n n n n n n n n n Q J Q K Q Q Q Q Q Q Q Q Q2 ___________ ___ 1 0 3 ___ 2 ___ 2 1 0 3 ___ ___ 2 2 1 2 2 n n n n n n n n n Q J Q K Q Q Q Q Q Q Q3 ___ 0 ___ 3 2 1 0 3 ___ 3 ___ 3 3 1 3 状态转换表如下表 8-3 所示: 画出状态转换图可得该电路为一十进制 加法计数器,且能自启动。 Q2 Q1 Q0 & & & Q J K Q Q J K Q Q J K Q Q J K Q Q3 1 1 1 清零 计数脉冲 图 8-16 1 2 n Q 1 1 n Q 1 0 n Q2 Q 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 1 1 1 0 Q3 Q1 Q0 1 3 n Q 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0 0 0 1 1 1 1 0 0 0 1 1 0 1 0 1 0 1 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0 0 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 表 8-3
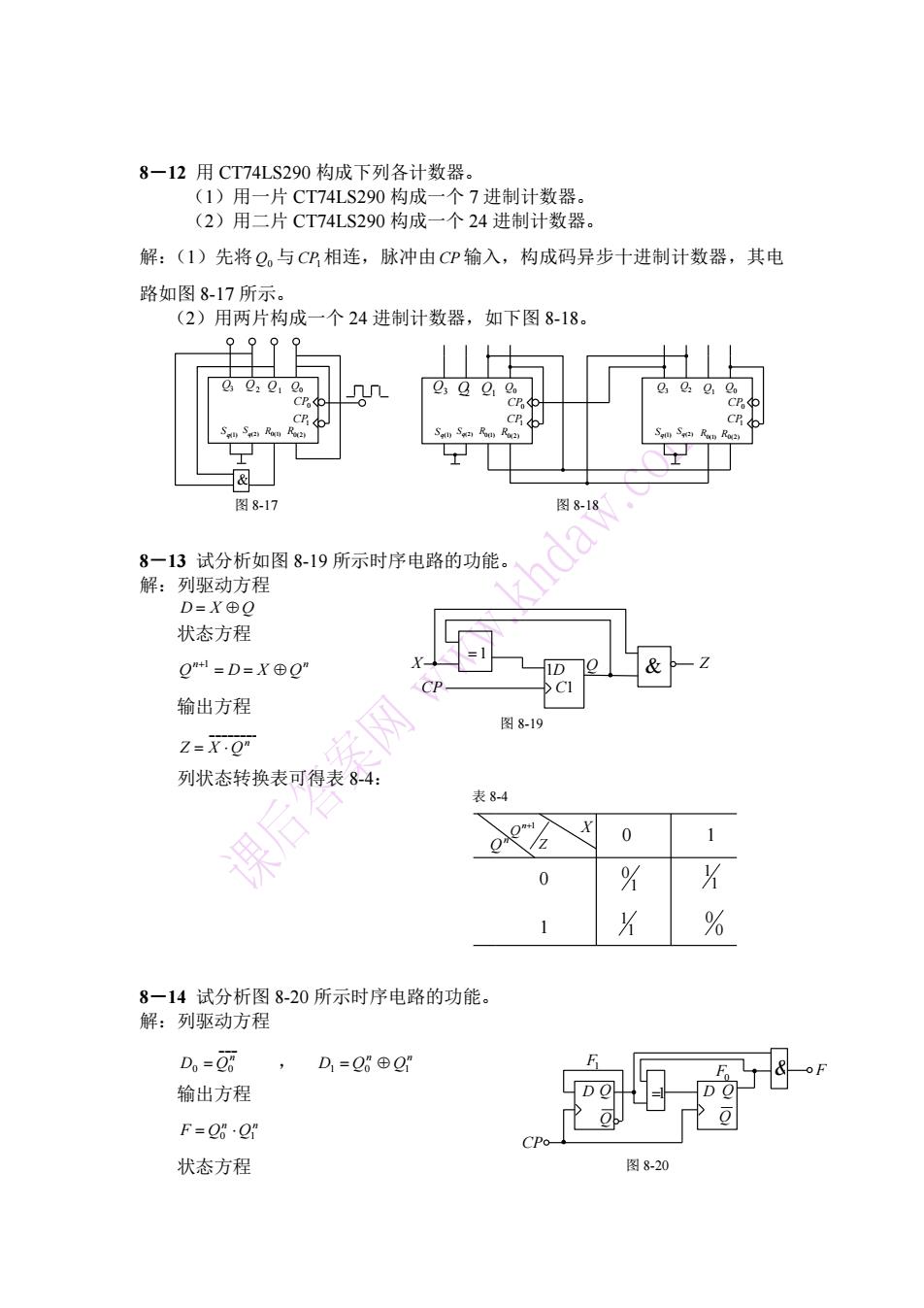
8-12用CT74LS290构成下列各计数器。 (1)用一片CT74LS290构成一个7进制计数器。 (2)用二片CT74LS290构成一个24进制计数器。 解:(1)先将Q。与CP相连,脉冲由CP输入,构成码异步十进制计数器,其电 路如图8-17所示。 (2)用两片构成一个24进制计数器,如下图8-18。 CP & 图8-17 图8-1& 8一13试分析如图8-19所示时序电路的功能。 解:列驱动方程 D=X⊕Q 状态方程 QH=D=X⊕Q” 输出方程 图8-19 Z=X.O 课后 列状态转换表可得表8-4: 表8-4 0 o' 0 % 片 1 X % 8一14试分析图8-20所示时序电路的功能。 解:列驱动方程 D。=Q8 ,D1=Q⊕Q1 输出方程 F=Q6·Q 邢 状态方程 图8-20
8-12 用 CT74LS290 构成下列各计数器。 (1)用一片 CT74LS290 构成一个 7 进制计数器。 (2)用二片 CT74LS290 构成一个 24 进制计数器。 解:(1)先将 Q0 与 CP1 相连,脉冲由 CP 输入,构成码异步十进制计数器,其电 路如图 8-17 所示。 (2)用两片构成一个 24 进制计数器,如下图 8-18。 8-13 试分析如图 8-19 所示时序电路的功能。 解:列驱动方程 D X Q 状态方程 n n Q D X Q 1 输出方程 ________ n Z X Q 列状态转换表可得表 8-4: 8-14 试分析图 8-20 所示时序电路的功能。 解:列驱动方程 ___ 0 0 n D Q , n n D1 Q0 Q1 输出方程 n n F Q0 Q1 状态方程 CP1 CP0 R0(1) Q3 Q2 Q1 Q0 Sq(1) Sq(2) R0(2) & 图 8-17 CP1 CP0 R0(1) Q3 Q2 Q0 Q1 Sq(1) Sq(2) R0(2) CP1 CP0 R0(1) Q3 Q2 Q1 Q0 Sq(1) Sq(2) R0(2) 图 8-18 图 8-19 CP X Q Z 1 & C1 1D & 1 F D Q D Q Q Q F0 F1 CP 图 8-20 1 0 0 1 1 0 0 0 1 1 1 1 X n Q Z Q n1 表 8-4