
第1单元能力训练检测题 一、填空题 1、由二值变量所构成的因果关系称为逻辑关系。能够反映和处理逻辑关系的 数学工具称为逻辑代数。 2、在正逻辑的约定下,“1”表示高电平,“0”表示低电平。 3、数字电路中,输入信号和输出信号之间的关系是逻辑关系,所以数字电路也称 为逻辑电路。在逻辑关系中,最基本的关系是与逻辑、或逻辑和非逻辑。 4、用来表示各种计数制数码个数的数称为基数,同一数码在不同数位所代表的 权不同。十进制计数各位的基数是10,位权是10的幂。 5、8421BCD码和2421码是有权码:余3码和格雷码是无权码。 6、进位计数制是表示数值大小的各种方法的统称。一般都是按照进位方式来实现 计数的,简称为数制。任意进制数转换为十进制数时,均采用按位权展开求和的方 法。 7、十进制整数转换成二进制时采用除2取余法:十进制小数转换成二进制时采用 乘2取整法。 8、十进制数转换为八进制和十六进制时,应先转换成二进制,然后再根据转换 的二进数,按照三个数码一组转换成八进制:按四个数码一组转换成十六 进制。 9、逻辑代数的基本定律有交换律、结合律、分配律、反演律和非非律。 10、最简与或表达式是指在表达式中与项中的变量最少,且或项也最少。 13、卡诺图是将代表最小项的小方格按相邻原则排列而构成的方块图。卡诺 图的画图规则:任意两个几何位置相邻的最小项之间,只允许一位变量的取值不同。 14、在化简的过程中,约束项可以根据需要看作1或0。 二、判断正误题 1、奇偶校验码是最基本的检错码,用来使用PCM方法传送讯号时避免出错。(对) 2、异或函数与同或函数在逻辑上互为反函数。 (对) 3、8421BCD码、2421BCD码和余3码都属于有权码。 (错) 4、二进制计数中各位的基是2,不同数位的权是2的幂。 (对) 3、每个最小项都是各变量相“与”构成的,即个变量的最小项含有n个因子。(对) 4、因为逻辑表达式A+B+AB=A+B成立,所以AB=O成立。 (错) 5、逻辑函数F=AB+AB+BC+BC己是最简与或表达式。 (错) 6、利用约束项化简时,将全部约束项都画入卡诺图,可得到函数的最简形式。(错) 7、卡诺图中为1的方格均表示逻辑函数的一个最小项。 (对)
1 第 1 单元 能力训练检测题 一、填空题 1、由二值变量所构成的因果关系称为 逻辑 关系。能够反映和处理 逻辑 关系的 数学工具称为逻辑代数。 2、在正逻辑的约定下,“1”表示 高 电平,“0”表示 低 电平。 3、数字电路中,输入信号和输出信号之间的关系是 逻辑 关系,所以数字电路也称 为 逻辑 电路。在 逻辑 关系中,最基本的关系是 与逻辑 、 或逻辑 和 非逻辑 。 4、用来表示各种计数制数码个数的数称为 基数 ,同一数码在不同数位所代表的 权 不同。十进制计数各位的 基数 是10, 位权 是10的幂。 5、 8421 BCD码和 2421 码是有权码; 余3 码和 格雷 码是无权码。 6、 进位计数制 是表示数值大小的各种方法的统称。一般都是按照进位方式来实现 计数的,简称为 数 制。任意进制数转换为十进制数时,均采用 按位权展开求和 的方 法。 7、十进制整数转换成二进制时采用 除2取余 法;十进制小数转换成二进制时采用 乘2取整 法。 8、十进制数转换为八进制和十六进制时,应先转换成 二进 制,然后再根据转换 的 二进 数,按照 三个数码 一组转换成八进制;按 四个数码 一组转换成十六 进制。 9、逻辑代数的基本定律有 交换 律、 结合 律、 分配 律、 反演 律和 非非 律。 10、最简与或表达式是指在表达式中 与项中的变量 最少,且 或项 也最少。 13、卡诺图是将代表 最小项 的小方格按 相邻 原则排列而构成的方块图。卡诺 图的画图规则:任意两个几何位置相邻的 最小项 之间,只允许 一位变量 的取值不同。 14、在化简的过程中,约束项可以根据需要看作 1 或 0 。 二、判断正误题 1、奇偶校验码是最基本的检错码,用来使用PCM方法传送讯号时避免出错。( 对 ) 2、异或函数与同或函数在逻辑上互为反函数。 ( 对 ) 3、8421BCD码、2421BCD码和余3码都属于有权码。 ( 错 ) 4、二进制计数中各位的基是2,不同数位的权是2的幂。 ( 对 ) 3、每个最小项都是各变量相“与”构成的,即n个变量的最小项含有n个因子。( 对 ) 4、因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。 ( 错 ) 5、逻辑函数F=A B + A B+ B C+B C 已是最简与或表达式。 ( 错 ) 6、利用约束项化简时,将全部约束项都画入卡诺图,可得到函数的最简形式。( 错 ) 7、卡诺图中为1的方格均表示逻辑函数的一个最小项。 ( 对 )

8、在逻辑运算中,“与”逻辑的符号级别最高。 (对) 9、标准与或式和最简与或式的概念相同。 (对) 10、二极管和三极管在数字电路中可工作在截止区、饱和区和放大区。 (错) 三、选择题 1、逻辑函数中的逻辑“与”和它对应的逻辑代数运算关系为(B)。 A、逻辑加 B、逻辑乘 C、逻辑非 2.、十进制数100对应的二进制数为(C)。 A、1011110 B、1100010 C、1100100 D、11000100 3、和逻辑式AB表示不同逻辑关系的逻辑式是(B)。 A、A+B B、A·B C、A·B+B D、AB+A 4、数字电路中机器识别和常用的数制是(A)。 A、二进制 B、八进制 C、十进制 D、十六进制 5、以下表达式中符合逻辑运算法则的是(D)。 A、C·C=C2 B、1+1=10 C、0<1 D、A+1=1 6、A+BC=(C)。 A、A+B B、A+C C、(A+B)(A+C) D、B+C 7、在(D)输入情况下,“与非”运算的结果是逻辑0。 A、全部输入是0B、任一输入是0 C、仅一输入是0 D、全部输入是1 四、简述题 1、逻辑代数与普通代数有何异同? 答:逻辑代数中仅含有0和1两个数码,普通代数含有的数码是0~9个,逻辑代数 是逻辑运算,普通代数是加、减、乘、除运算。 2、什么是最小项?最小项具有什么性质? 答:一个具有个逻辑变量的与或表达式中,若每个变量以原变量或反变量形式仅出 现一次,就可组成2"个“与”项,我们把这些“与”项称为个变量的最小项,分别记为 mn。最小项具备下列性质: ①对于任意一个最小项,只有一组变量取值使它的值为1,而变量取其余各组值时, 该最小项均为0。 ②任意两个不同的最小项之积恒为0。 ③变量全部最小项这和恒等于1。 3、试述卡诺图化简逻辑函数的原则和步骤。 答:利用卡诺图化简逻辑函数式的步骤: ①根据变量的数目,画出相应方格数的卡诺图: 2
2 8、在逻辑运算中,“与”逻辑的符号级别最高。 ( 对 ) 9、标准与或式和最简与或式的概念相同。 ( 对 ) 10、二极管和三极管在数字电路中可工作在截止区、饱和区和放大区。 ( 错 ) 三、选择题 1、逻辑函数中的逻辑“与”和它对应的逻辑代数运算关系为( B )。 A、逻辑加 B、逻辑乘 C、逻辑非 2.、十进制数100对应的二进制数为( C )。 A、1011110 B、1100010 C、1100100 D、11000100 3、和逻辑式 AB 表示不同逻辑关系的逻辑式是( B )。 A、 A B B、 A B C、 A B B D、 AB A 4、数字电路中机器识别和常用的数制是( A )。 A、二进制 B、八进制 C、十进制 D、十六进制 5、以下表达式中符合逻辑运算法则的是( D )。 A、C·C=C2 B、1+1=10 C、0<1 D、A+1=1 6、A+BC=( C )。 A、A+B B、A+C C、(A+B)(A+C) D、B+C 7、在( D )输入情况下,“与非”运算的结果是逻辑 0。 A、全部输入是0 B、任一输入是0 C、仅一输入是0 D、全部输入是1 四、简述题 1、逻辑代数与普通代数有何异同? 答:逻辑代数中仅含有 0 和 1 两个数码,普通代数含有的数码是 0~9 个,逻辑代数 是逻辑运算,普通代数是加、减、乘、除运算。 2、什么是最小项?最小项具有什么性质? 答:一个具有n个逻辑变量的与或表达式中,若每个变量以原变量或反变量形式仅出 现一次,就可组成2 n个“与”项,我们把这些“与”项称为n个变量的最小项,分别记为 mn。最小项具备下列性质: ①对于任意一个最小项,只有一组变量取值使它的值为1,而变量取其余各组值时, 该最小项均为0。 ②任意两个不同的最小项之积恒为0。 ③变量全部最小项这和恒等于1。 3、试述卡诺图化简逻辑函数的原则和步骤。 答:利用卡诺图化简逻辑函数式的步骤: ①根据变量的数目,画出相应方格数的卡诺图;

②根据逻辑函数式,把所有为“1”的项画入卡诺图中: ③用卡诺圈把相邻最小项进行合并,合并时就遵照卡诺圈最大化原则: ④根据所圈的卡诺圈,消除圈内全部互非的变量,每一个圈作为一个“与”项,将 各“与”项相或,即为化简后的最简与或表达式。 五、计算题 1、用代数法化简下列逻辑函数 ①F=(A+B)C+AB F=(A+B)C+AB AC+BC+AB 解: =CAB+AB =C+AB ②F=AC+AB+BC F=AC+AB+BC 解: AC+BCA =AC+B 3F=ABC+ABC+ABC+ABC+ABC F=ABC+ABC+ABC+ABC+ABC 解: =AB+AB+AC F=AB+BCD+C D+ABC +ACD F=AB+BCD+C D+ABC +ACD 解: =AB+AC+CD+BC =AB+ABC+ABC+CD+BC =AB+CD+BC 2、用卡诺图化简下列逻辑函数 ①F(AB.C,D)=Sm(3.4.5,7,9,13,14,15) F=ABC+ACD+ACD+ABC CD AB 0001 11 10 00 1 01 11) 1 1 10 3
3 ②根据逻辑函数式,把所有为“1”的项画入卡诺图中; ③用卡诺圈把相邻最小项进行合并,合并时就遵照卡诺圈最大化原则; ④根据所圈的卡诺圈,消除圈内全部互非的变量,每一个圈作为一个“与”项,将 各“与”项相或,即为化简后的最简与或表达式。 五、计算题 1、用代数法化简下列逻辑函数 ① F (A B)C AB 解: C AB CAB AB AC BC AB F A B C AB ( ) ② F AC AB BC 解: AC B AC BCA F AC AB BC ③ F ABC ABC ABC ABC ABC 解: AB AB AC F ABC ABC ABC ABC ABC ④ F AB BCD C D ABC ACD 解: AB CD BC AB ABC ABC CD BC AB AC CD BC F AB BCD C D ABC ACD 2、用卡诺图化简下列逻辑函数 ①F(A, B, C, D)= ∑m(3, 4, 5, 7, 9, 13, 14, 15) F ABC ACD ACD ABC CD AB 1 1 1 1 1 1 1 1 00 01 11 10 00 01 11 10
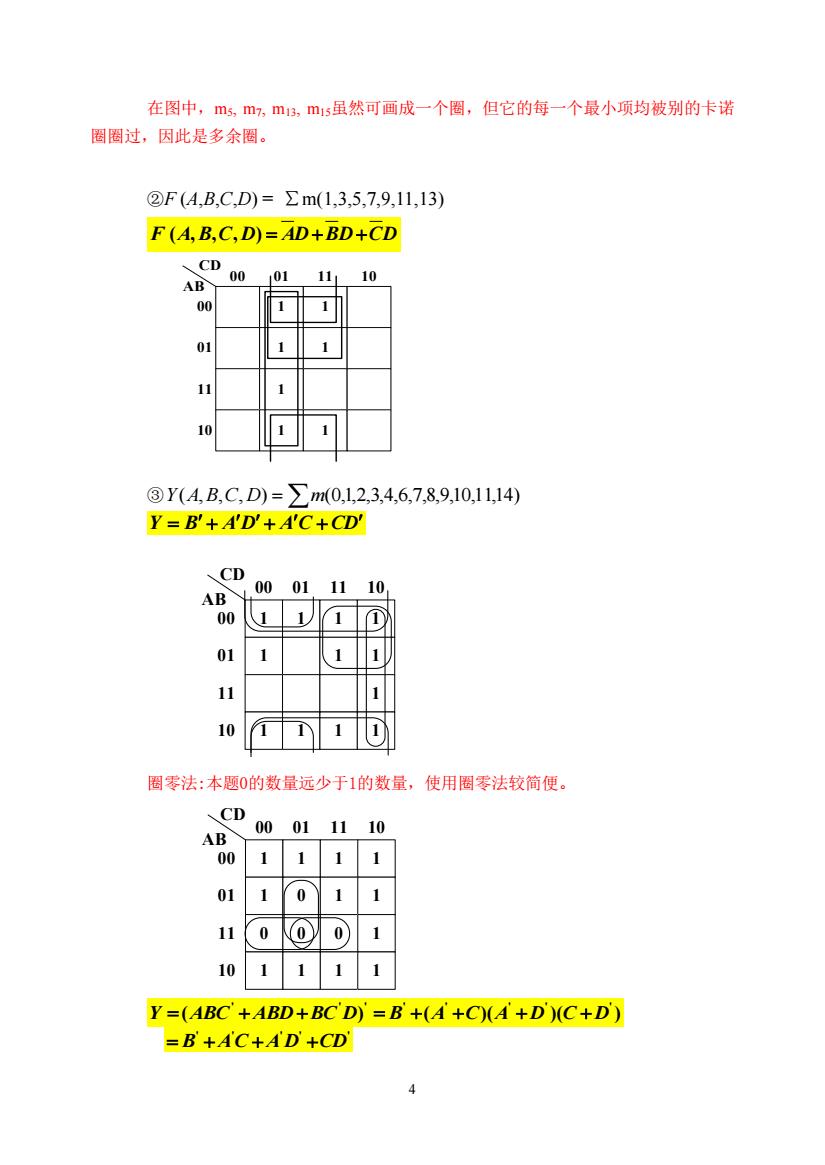
在图中,ms,m,m,m15虽然可画成一个圈,但它的每一个最小项均被别的卡诺 圈圈过,因此是多余圈。 ②F(A,B,C,D)=∑m(1,3,57,9,11,13) F (A,B,C,D)=AD+BD+CD 、CD 00 01 11 10 AB 00 01 1 1 11 10 ③Y(AB,C,D)=∑m(0,1,2,3,4,6,7,8,9,10,11,14) Y=B'+A'D'+A'C+CD' 、CD 00 0111 10 AB 00 1 01 1 1 11 10 圈零法:本题0的数量远少于1的数量,使用圈零法较简便。 、CD 00 01 11 10 AB 00 01 11 10 Y=(ABC+ABD+BC'D)=B+(A+C)(A+D)(C+D) =B+AC+AD+CD
4 在图中,m5, m7, m13, m15虽然可画成一个圈,但它的每一个最小项均被别的卡诺 圈圈过,因此是多余圈。 ②F (A,B,C,D) = ∑m(1,3,5,7,9,11,13) F (A,B,C, D) AD BD CD ③ Y(A,B,C,D) m(0,1,2,3,4,6,7,8,9,10,11,14) Y B AD AC CD 圈零法:本题0的数量远少于1的数量,使用圈零法较简便。 ' ' ' Y (ABC ABD BC D) ( )( )( ) ' ' ' ' ' B A C A D C D ' ' ' ' ' B AC A D CD 1 1 1 1 1 1 1 00 01 11 10 00 01 CD AB 1 1 1 1 1 11 10 1 1 1 1 1 0 1 1 00 01 11 10 00 01 CD AB 0 0 0 1 1 1 1 1 11 10 00 1 01 00 01 AB CD 1 1 1 11 10 11 1 10 1 1

3、完成下列数制之间的转换 ①(365)10=(101101101)2=(555)8=(16D)16 ②(11101.1)2=(29.5)10=(35.4)8=(1D.8)16 ③(57.625)10=(111001.101)2=(71.5)8=(39.A)16 4、完成下列数制与码制之间的转换(6分) ①(47)10=(01000111)8421跨 ②(25.25)10=(00100101.00120101)821Bm=(31.2)8 5
5 3、完成下列数制之间的转换 ①(365)10=( 101101101 )2=(555 )8=(16D )16 ②(11101.1)2=(29.5)10=( 35.4)8=(1D.8)16 ③(57.625)10=(111001.101)2=(71.5 )8=( 39.A )16 4、完成下列数制与码制之间的转换(6分) ①(47)10=( 01000111 )8421码 ②(25.25)10=( 00100101.00120101 )8421BCD =(31.2)8