
ME369 Modeling,Analysis and System Control-A --Lecture 141027 Week 7# Ch5.3~5. Oct.27(M) Transient,second order system, spec. 6 Transient,higher order system Ch5.45. 0ct.29(W) HW4 Stability,Routh Criterion 7 Week 8# Routh Criterion Ch5.7 Nov.3(M) HW3 due Steady State Error Ch5.8 Practical lecture 1-control Nov.5(W) system modeling Quiz 2
ME369 Modeling, Analysis and System Control-A --Lecture_141027 Week 7# Oct.27(M) Transient, second order system, spec. Ch5.3~5. 6 Oct.29(W) Transient, higher order system Stability, Routh Criterion Ch5.4~5. 7 HW4 Week 8# Nov.3(M) Routh Criterion Steady State Error Ch5.7 Ch5.8 HW3 due Nov.5(W) Practical lecture 1 – control system modeling Quiz 2

Outline of today's PPT file Transient Response of Second-Order Systems ·二阶系统的瞬态响应 Step response Ramp response Transient Response Analysis and Specification
Outline of today’s PPT file • Transient Response of Second-Order Systems • 二阶系统的瞬态响应 – Step response – Ramp response • Transient Response Analysis and Specification
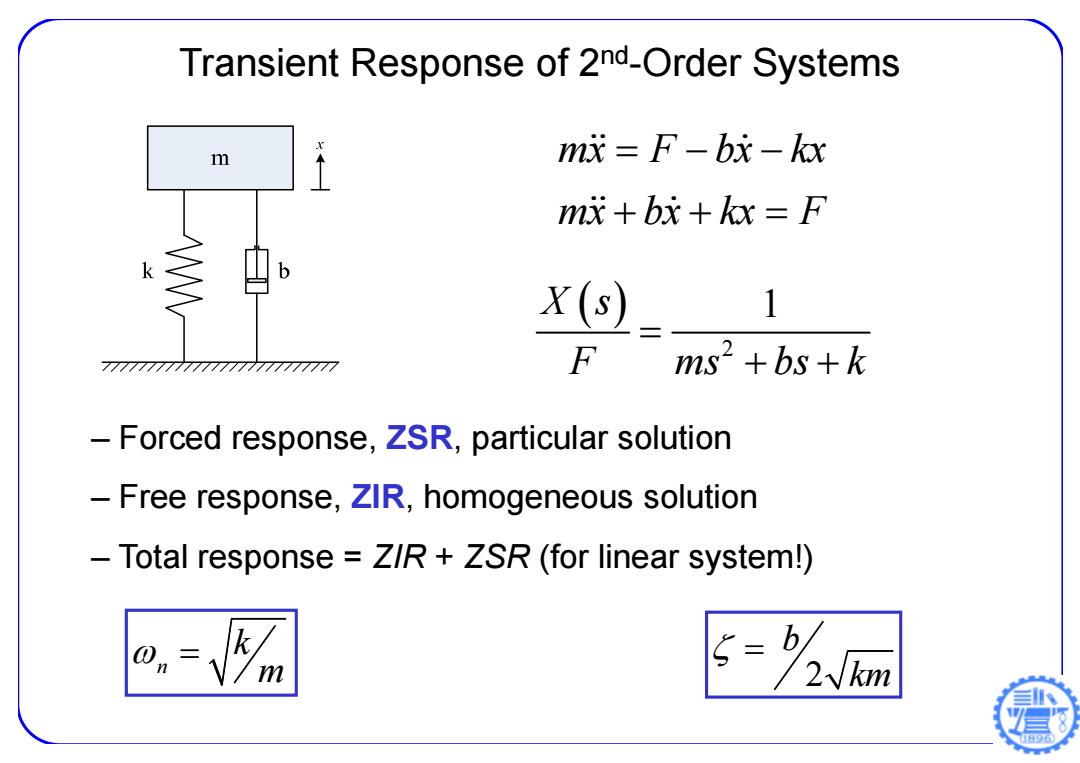
Transient Response of 2nd-Order Systems m m成=F-bx-x mx+bx+kx=F X(s) 1 7777777777777777777777777 F ms2 +bs+k -Forced response,ZSR,particular solution Free response,ZIR,homogeneous solution Total response Z/R+ZSR(for linear system!) 5= 日96
Transient Response of 2nd-Order Systems mx F bx kx mx bx kx F 2 X s 1 F ms bs k – Forced response, ZSR, particular solution – Free response, ZIR, homogeneous solution – Total response = ZIR + ZSR (for linear system!) n k m 2 b km

Free Response )+250n)+oy=0 I.C.y(0),(0) → [s2Y(s)-y(0)-(0)]+250n[sY(s)-y(0)]+o,Y(s)=0 s=-0+j@d Damped natural frequency Y(s)= (s+250n)y(0)+(0) 阻尼自然频率 → s2+250nS+0n o=Cw,:wj=wV1-52 S+σ > Y(s)=a(s+a)+0j +6 (s+o)2+o → Y(s)=0)+0) @a S+O @d +o+a+X0 s+o)2+o7 → 0=g0+0e"sino,1+X0ecosa,1 @a 日96
Free Response 2 2 0 n n y yy I.C. (0), (0) y y 2 2 [ ( ) (0) (0)] 2 [ ( ) (0)] ( ) 0 n n s Y s sy y sY s y Y s 2 2 ( 2 ) (0) (0) ( ) 2n n n s y y Y s s s 22 22 ( ) () () d d d s Y s a s s b 22 22 ( ) ( ) (0) (0 ) ( ) (0 ) d d d d y y s s s y s Y (0) (0) ( ) sin (0) cos t t d d d yt e t e y y y t 2 ; 1 s zw w w z = =- nd n d s j Damped natural frequency 阻尼自然频率

Solutions for 2nd Order Systems x()◆ )+250ny+o元y=u(t) x(0) 0<<1 =1 g>1 0 5>1 Overdamped 5=1 Critically damped 0<<1 Underdamped
Solutions for 2nd Order Systems 2 2 () n n y y y ut 1 1 0 1 Overdamped Critically damped Underdamped