上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源（讲义课件）Lecture_141027

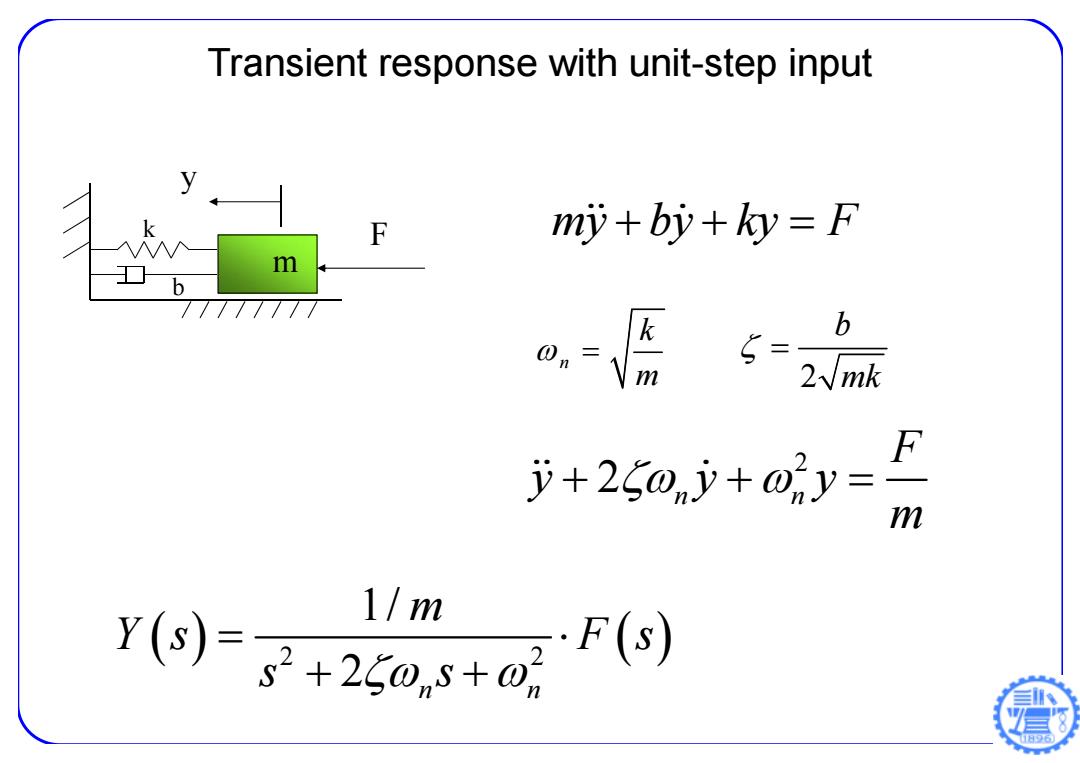
Transient response with unit-step input F my+bi+ky=F m b b @.-Vm 2√mk +250n少+o7y= kS 1/m y(o)s+25os+@(

F m y k b m  y   by  ky  F n k m   2 b mk   2 2 n n F y yy m           2 2 1/ 2 n n m Ys Fs s s       Transient response with unit-step input

Transient response with unit-step input Standard expression +250n立+o7y=ou(t) Roots are S1,2=±j0m c(t) y(t)=1-cos(@,t) 2 Free vibration Critically stable 5=0 Without damping零阻尼

Transient response with unit-step input 2 2 2 () nn n   y y y ut        0 Without damping 零阻尼 Roots are n s 1,2   j  2 2 2 () () n n Ys Us s     y ( t ) 1 cos( t )   n Free vibration Critically stable Standard expression

Transient response with unit-step input j9+250n少+07y=07u(t) Roots are s.2=-50n±j0nV1-52=-60n±j0a Damped natural frequency 阻尼自然频率 213816412 1 0.2 0.4 Rs)s 0.6 ξ=0.8 c(t)=1- s:0 sin@,1+A)(e0) B=g-5 tp 5 10 15 0<5<1 Underdamped (欠阻尼)

Roots are 0   1 Underdamped (欠阻尼) n n n d s    j      j 2 1,2 1 sin( ) 1 ( ) 1 2          t e c t d t n (t0) 2 d n 1 Damped natural frequency 阻尼自然频率 s R s 1 ( )     2 1 1   tg Transient response with unit-step input 2 2 2 () nn n   y y y ut     

5.2=-g0n±j0nV1-52=-50n±j0a c(0=1- -sno,i+B jo (t≥0) S平面 B 04=0nV1-52 B=你个≤ 日6

2  d   n 1  sin( ) 1 ( ) 1 2          t e c t d t n (t0)    2 1 1   tg n n n d s    j      j 2 1,2 1

Transient response with unit-step input +250n少+oy=ou(t) Roots are 2=-0n±0nV52-1 Rising monotone,without vibration,long transient reponse,can be divided as two first-order systems. 5>1 Overdamped

Roots are  1 Overdamped 1 2 P1、2  n n   Rising monotone, without vibration, long transient reponse, can be divided as two first-order systems. Transient response with unit-step input 2 2 2 () nn n   y y y ut     