
ME369 Modeling,Analysis and System Control Fall 2014 Yuan Jianjun(袁建军) Associate Professor,Robotics Institute Office:Room 401,Building B of ME School yuanjj@sjtu.edu.edu.cn 021-34205559
Yuan Jianjun (袁建军) Associate Professor, Robotics Institute Office: Room 401, Building B of ME School yuanjj@sjtu.edu.edu.cn 021-34205559 ME369 Modeling, Analysis and System Control Fall 2014
ME369 Modeling,Analysis and System Control-A --Lecture 140917 Week 1# Administrative Issues Sep.15(M) Ch1 Introduction to control system Sep.17(W) Laplace Transform-definition, Ch2.1~ 2.4(4) HW1 theorems Week 2# Sep.22(M) Laplace Transform-inverse, Ch2.4, solving equation,MATLAB 2.5(4h) Dynamic systems-mechanical Ch3.1 HW1 due Sep.24(W) electrical system modeling 3.3 HW2
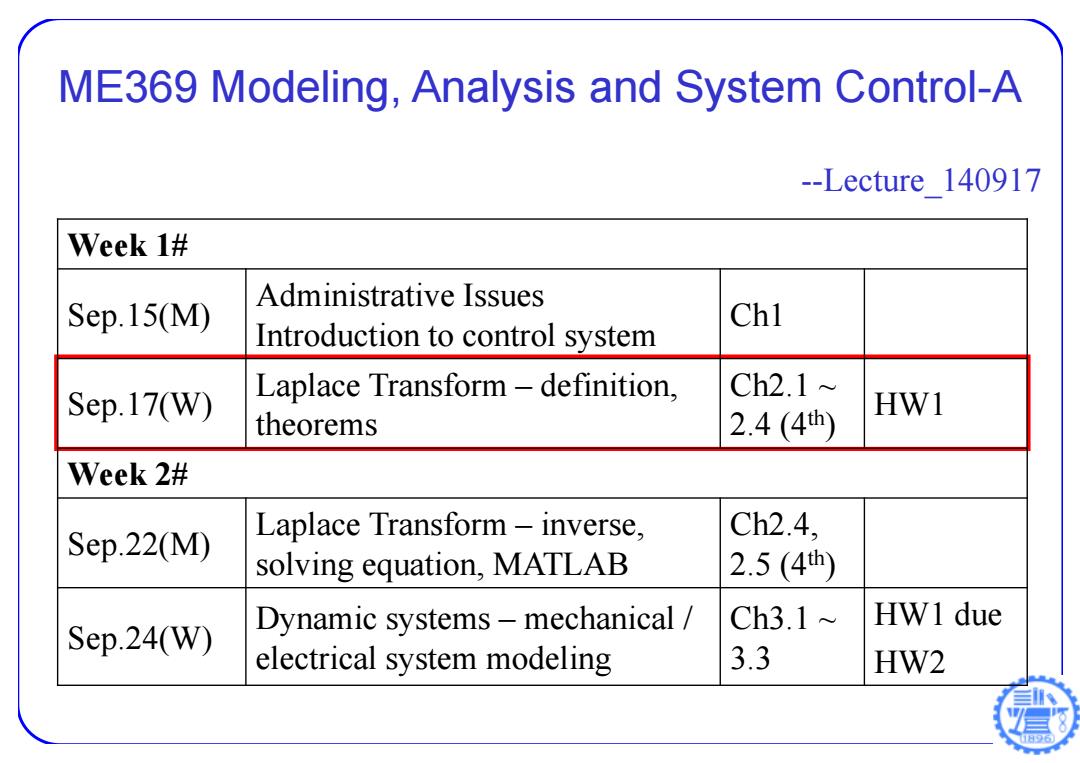
ME369 Modeling, Analysis and System Control-A --Lecture_140917 Week 1# Sep.15(M) Administrative Issues Introduction to control system Ch1 Sep.17(W) Laplace Transform – definition, theorems Ch2.1 ~ 2.4 (4th ) HW1 Week 2# Sep.22(M) Laplace Transform – inverse, solving equation, MATLAB Ch2.4, 2.5 (4th ) Sep.24(W) Dynamic systems – mechanical / electrical system modeling Ch3.1 ~ 3.3 HW1 due HW2

Problems of HW1 ·Refer to the ftp site. .ftp://public.sjtu.edu.cn ·User:yuanjj ·Password:public DUE:Sep.24 (W)
Problems of HW1 • Refer to the ftp site. • ftp://public.sjtu.edu.cn • User: yuanjj • Password: public DUE: Sep.24 (W)

Definition of Laplace Transform Definition of Laplace Transform The Laplace Transform of f(t)is defined as F(s)=f(t)e-dt=[f() S=0+j0 Function ft)that satisfies 1.A time continuous function; 2.Real function; 3.t)=0,for0: 4 0f(t)eh<w→limf()e=0
• Definition of Laplace Transform • The Laplace Transform of f(t) is defined as 0 ( ) ( ) [ ( )] st F s f t e dt f t L lim ( ) 0 st t f te 0 ( ) st f t e dt Definition of Laplace Transform s j Function f(t) that satisfies 1. A time continuous function; 2. Real function; 3. f(t)=0, for t<0; 4

Laplace Transform of Typical Function 1.Exponential Function- 4.Sinusoidal Function [f(t)=0 for t<0 f(t)=0 for t<0 f(t)=Ae-for t≥0 f(t)=Asin ot for t≥0 2.Step Function f(t)=0 for t<0 ww-Sudv+Svdu f(t)=A for t≥0 3.Ramp Function Euler's Theorem f(t)=0 for t<0 f(t)=At for t≥0 coso1-em+em)
Laplace Transform of Typical Function 2. Step Function ( ) for 0 ( ) 0 for 0 f t A t f t t 3. Ramp Function ( ) for 0 ( ) 0 for 0 f t At t f t t uv udv vdu ( ) sin for 0 ( ) 0 for 0 f t A t t f t t 1.Exponential Function- 4. Sinusoidal Function ( ) for 0 ( ) 0 for 0 f t Ae t f t t t Euler’s Theorem