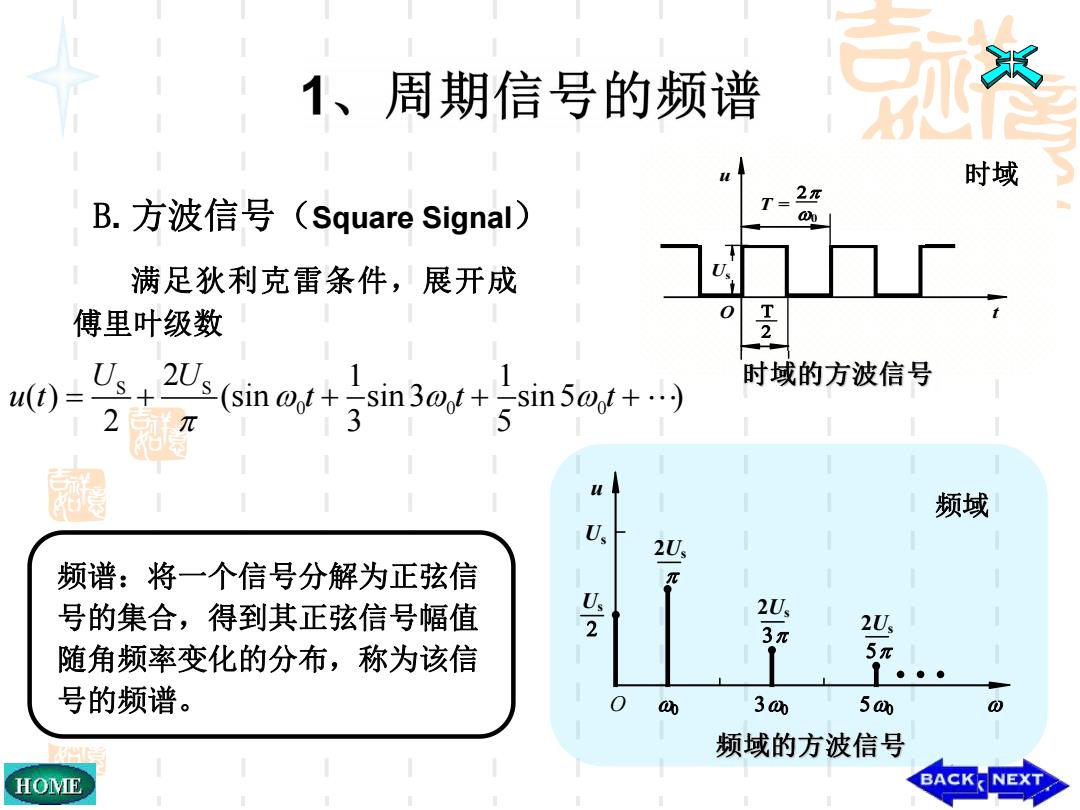
1、周期信号的频谱 时域 B.方波信号(Square Signal) T=27 满足狄利克雷条件,展开成 傅里叶级数 2 1 u(t)= 1 时域的方波信号 (sin ot+sin3@o+-sin5@o+) 2 频域 U, 2U, 频谱:将一个信号分解为正弦信 π 号的集合,得到其正弦信号幅值 受 2U, 3π 2U, 随角频率变化的分布,称为该信 5π ●●● 号的频谱。 心 300 500 频域的方波信号 HOME BACK NEXT
B. 方波信号(Square Signal) S S 0 0 0 2 1 1 ( ) (sin sin 3 sin 5 ) 2 3 5 U U u t t t t 时域 O 0 T = t u 满足狄利克雷条件,展开成 Us 傅里叶级数 频域 O 2Us Us Us 2Us 2Us u 频谱:将一个信号分解为正弦信 号的集合,得到其正弦信号幅值 随角频率变化的分布,称为该信 号的频谱
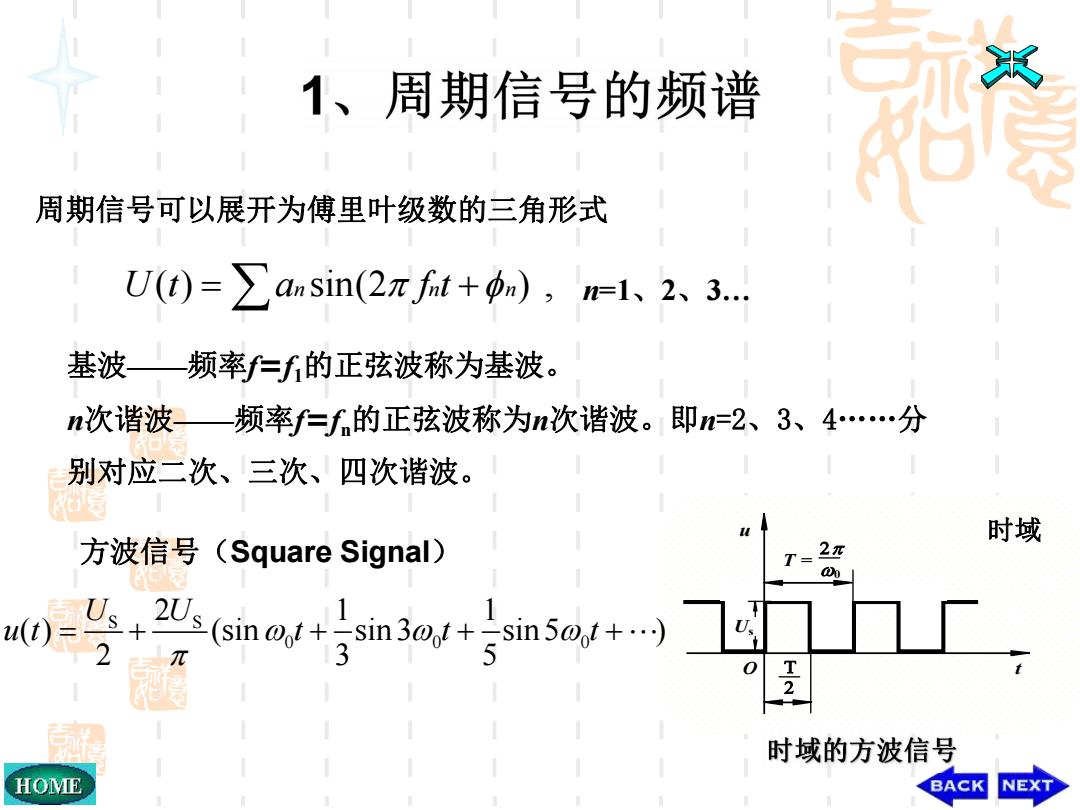
1、周期信号的频谱 周期信号可以展开为傅里叶级数的三角形式 U(t))=∑anSin(2πft+m),=l、2、3. 基波—频率f=的正弦波称为基波。 n次谐波一频率f=fn的正弦波称为n次谐波。即n=2、3、4…分 别对应二次、三次、四次谐波。 时域 方波信号(Square Signal) T=2z u(t)∈ 2((sin@f+5in3az+5sn5o+…)□s☐ 时域的方波信号 HOME BACK NEXT
U(t) an sin(2 fnt n) , n=1、2、3… 基波——频率f=f1的正弦波称为基波。 n次谐波——频率f=fn的正弦波称为n次谐波。即n=2、3、4……分 别对应二次、三次、四次谐波。 周期信号可以展开为傅里叶级数的三角形式 方波信号(Square Signal) 时域 O 0 T = t Us u S S 0 0 0 2 1 1 ( ) (sin sin 3 sin 5 ) 2 3 5 U U u t t t t
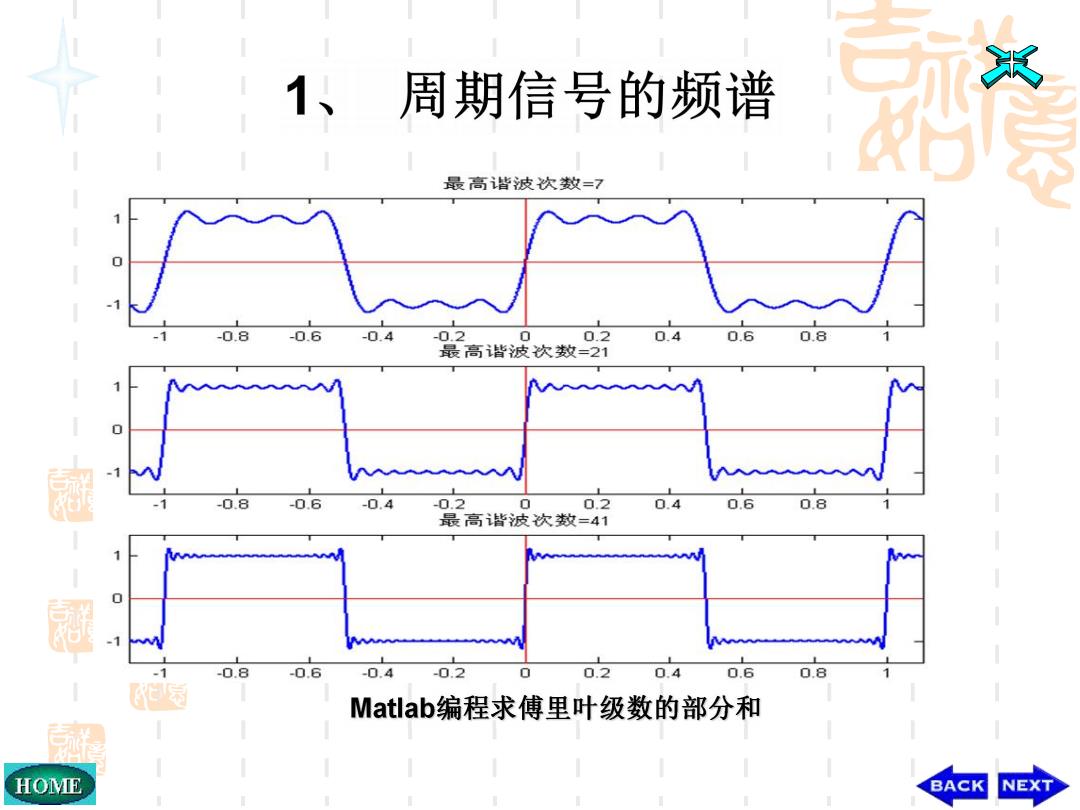
周期信号的频谱 最高谐波次数=7 -0.8 -0.6-0.4-0.2 0 0.2 0.40.6 0.8 最高皆波次数=21 -0.8 -0.6 -0.4 -0. 0 0.2 0.4 0.6 0.8 最高皆波次数=41 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 园 Matlab编程求傅里叶级数的部分和 HOME BACK NEXT
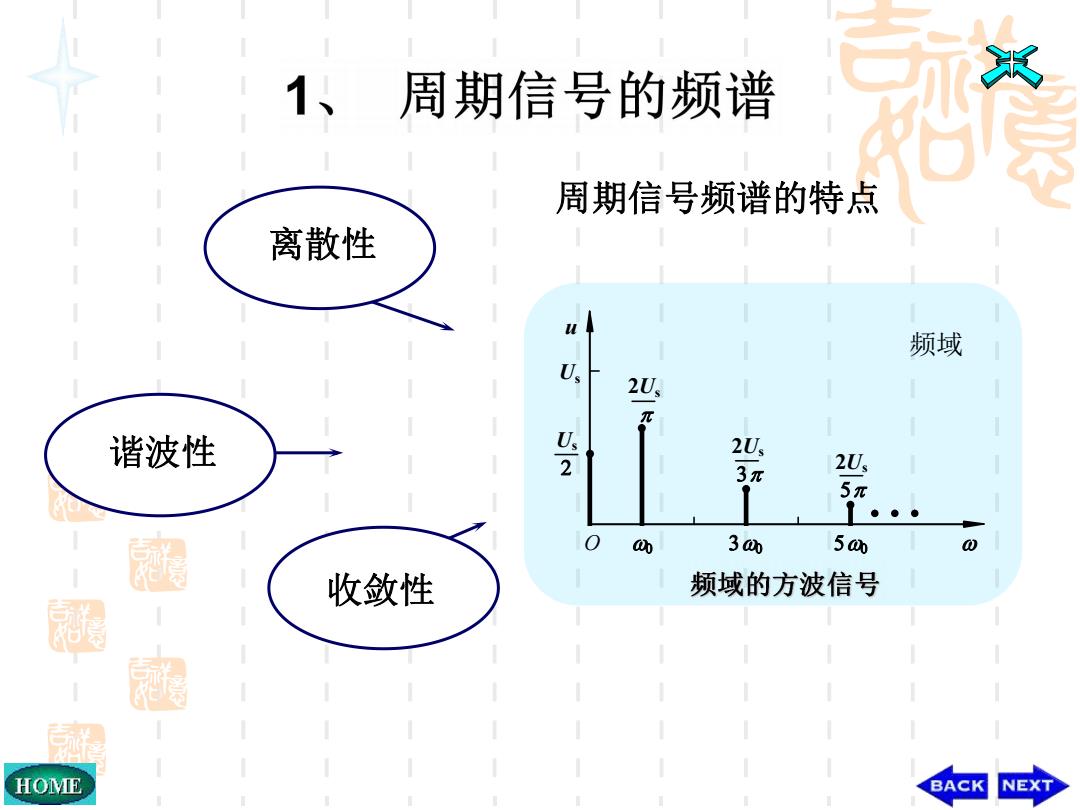
周期信号的频谱 周期信号频谱的特点 离散性 频域 U 20 π 谐波性 2U, 3π 20 5π ●●● 300 5 0 收敛性 频域的方波信号 凝 HOME BACK NEXT
离散性 谐波性 收敛性 周期信号频谱的特点 频域 O 2Us Us Us 2Us 2Us u
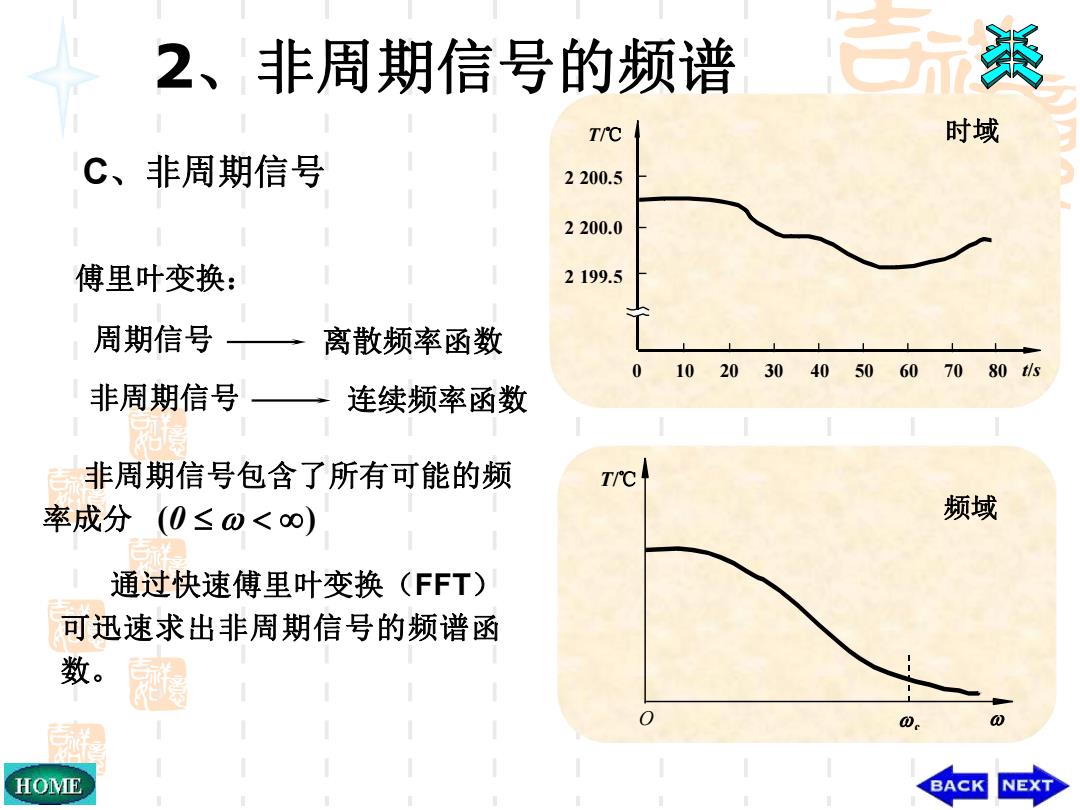
2、非周期信号的频谱 百玩英 T/℃ 时域 C、非周期信号 2200.5 2200.0 傅里叶变换: 2199.5 周期信号一 离散频率函数 0 1020304050607080ts 非周期信号一 连续频率函数 非周期信号包含了所有可能的频 T/℃ 率成分(0≤0<∞) 频域 通过快速傅里叶变换(FFT) 可迅速求出非周期信号的频谱函 数。 0 HOME BACK NEXT
非周期信号包含了所有可能的频 率成分 (0 ) C、非周期信号 傅里叶变换: 通过快速傅里叶变换(FFT) 可迅速求出非周期信号的频谱函 数。 周期信号 离散频率函数 非周期信号 连续频率函数 频域 O T/℃ c T/℃ 时域 2 200.5 2 200.0 2 199.5 0 10 20 30 40 50 60 70 80 t/s 2、非周期信号的频谱