
(2)多层平壁(2为常数、无内热源) 多层平壁的总热阻等于各层热阻之和 tn -tp X h 台,h2
(2) 多层平壁( 为常数、无内热源) 多层平壁的总热阻等于各层热阻之和 + + − = = 2 2 1 1 1 2 m W 1 1 h h t t q n i i i f f
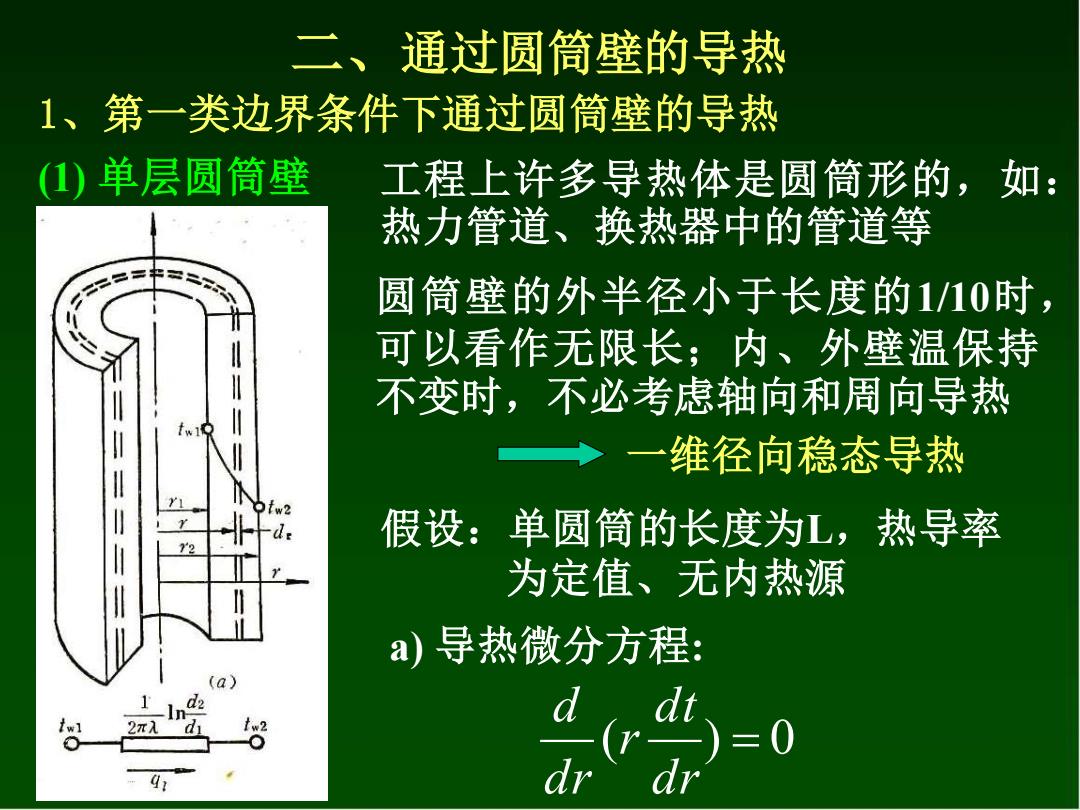
二、通过圆筒壁的导热 1、第一类边界条件下通过圆简壁的导热 (1)单层圆筒壁 工程上许多导热体是圆筒形的,如: 热力管道、换热器中的管道等 三平、 圆筒壁的外半径小于长度的1/10时, 可以看作无限长;内、外壁温保持 不变时,不必考虑轴向和周向导热 一维径向稳态导热 d 假设:单圆筒的长度为L,热导率 为定值、无内热源 a)导热微分方程: 2π =0
二、通过圆筒壁的导热 工程上许多导热体是圆筒形的,如: 热力管道、换热器中的管道等 一维径向稳态导热 a) 导热微分方程: 1、第一类边界条件下通过圆筒壁的导热 (1) 单层圆筒壁 圆筒壁的外半径小于长度的1/10时, 可以看作无限长;内、外壁温保持 不变时,不必考虑轴向和周向导热 假设:单圆筒的长度为L,热导率 为定值、无内热源 ( ) = 0 dr dt r dr d

a)导热微分方程: 之二三三三 )=0 b)几何条件:单层圆筒壁;1,2 c)物理条件:入已知;无内热源 -d: 2 d)时间条件:稳态导热:at/Ox=0 e)边界条件:=r1,t仁twi;Fr2,仁twl a 8 2π入 =c→t=Ghr+c, dr t =cIn n +c2;tw2 =c+c2 C1= In(r, C2 tim -(tw2-tu) n(r,n)
b) 几何条件:单层圆筒壁;r1 , r2 c) 物理条件: 已知;无内热源 e) 边界条件:r= r1 , t= tw1 ; r= r2 , t= tw1 d) 时间条件: a) 导热微分方程: ( ) = 0 dr dt r dr d 稳态导热 :t = 0 1 1 2 c t c ln r c d r d t r = = + 1 1 1 2 2 1 2 2 t c ln r c ; t c ln r c w = + w = + ln( ) ln ; ( ) ln( ) 2 1 1 2 1 2 1 2 1 2 1 1 r r r c t t t r r t t c w w w w w = − − − =
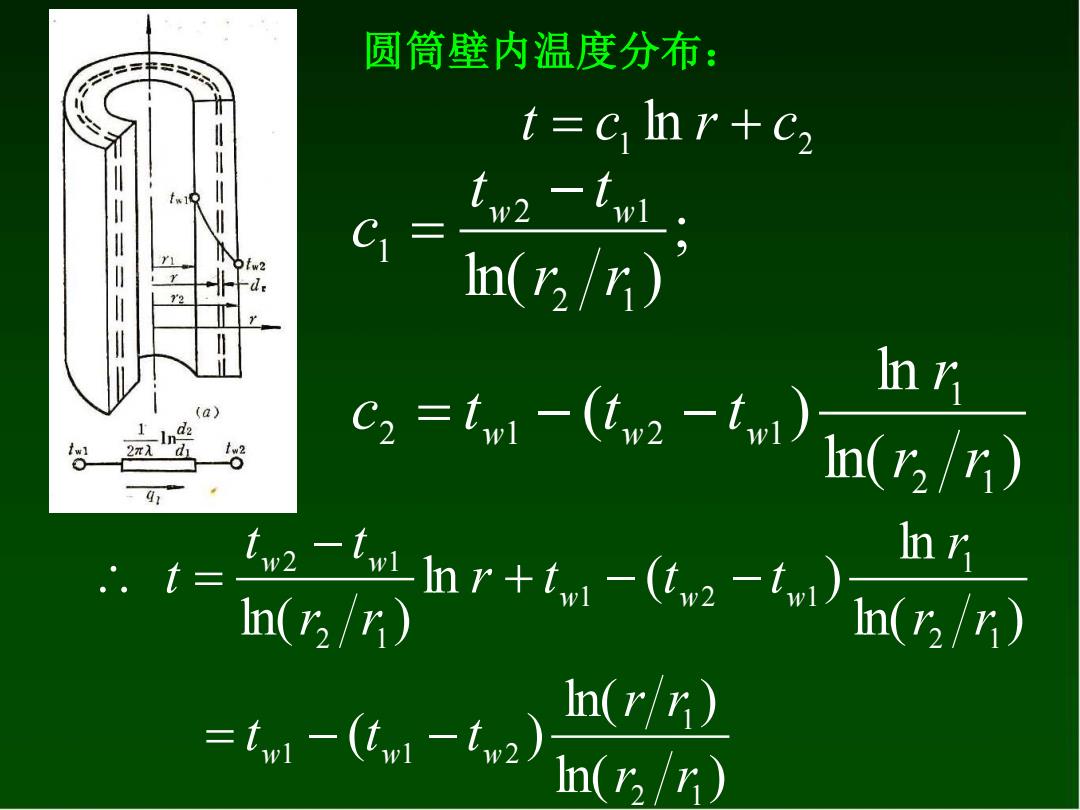
圆筒壁内温度分布: t=cmr+c2 tw2 -twl 6= 2 de n(5/r) Inr (a) lng 2πλd c,=t-t:-l n(2/r) 91 .t= tw2-tL In(r/r) r4o-t-ar,d n In(r) =tiel -(tw -tw2) n(2/r)
1 2 t = c ln r + c ln( ) ln ( ) ; ln( ) 2 1 1 2 1 2 1 2 1 2 1 1 r r r c t t t r r t t c w w w w w = − − − = 圆筒壁内温度分布: ln( ) ln( ) ( ) ln( ) ln ln ( ) ln( ) 2 1 1 1 1 2 2 1 1 1 2 1 2 1 2 1 r r r r t t t r r r r t t t r r t t t w w w w w w w w = − − + − − − =

圆筒壁内温度分布: 二三三三、 t=to1-(1-t2) In(r/) n(2/r) fw1 圆筒壁内温度分布曲线的形状? dttm-t2 1.d'tt twl -tw2 I 72 dr In(/n)r'dr2 In(r/r)r2 若t1>t2: d't >0 向上凹 a 2π 01 若tn<t2 <0 向下凹 -停小 t -tw2 _bo -tv2 w 1 In R 2π2
圆筒壁内温度分布: ln( ) ln( ) ( ) 2 1 1 1 1 2 r r r r t t t t = w − w − w 2 2 1 1 2 2 2 2 1 1 2 1 ln( ) ; 1 ln( ) r r r t t d r d t r r r t t d r d t w w w − w = − = − 圆筒壁内温度分布曲线的形状? 若 : 2 0 向上凹 2 1 2 d r d t t t w w 若 : 2 0 向下凹 2 1 2 d r d t t t w w W ln 2 1 1 ln( ) 2 1 2 1 2 1 2 2 1 1 2 R t t r r L t t r r r t t r L d r d t Φ A w w w w w − w = − = − = − = − −