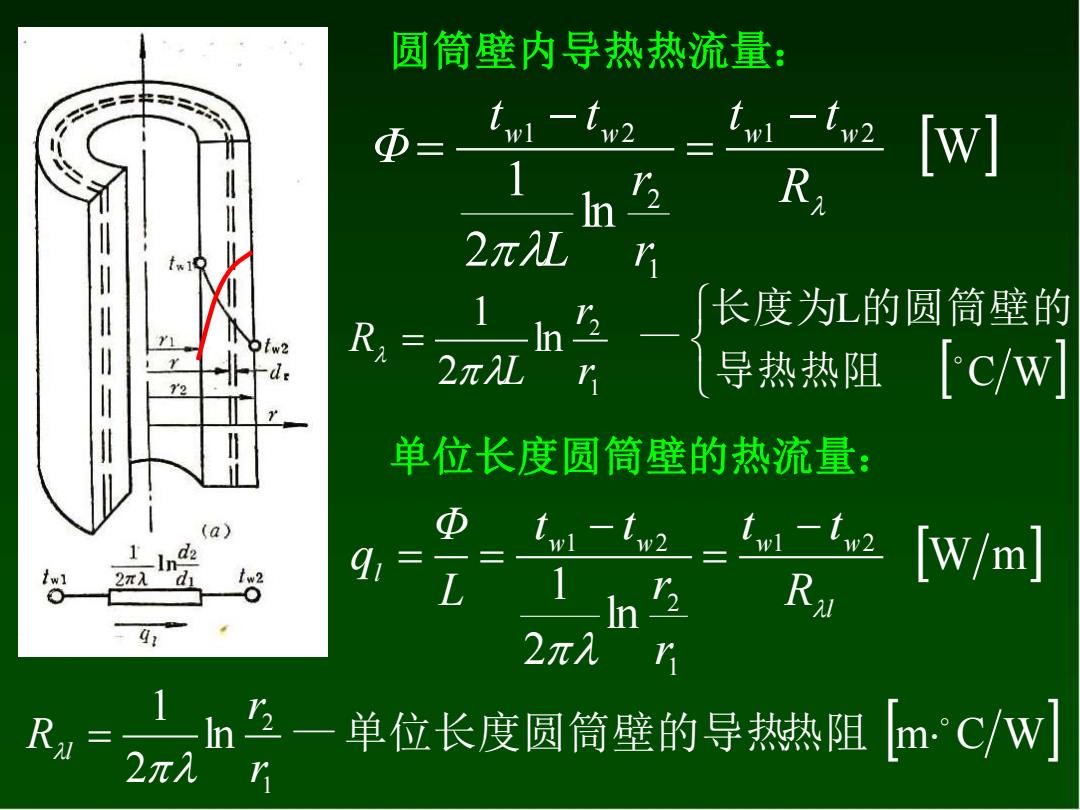
圆筒壁内导热热流量: 的二三=书一一 Φ= tim -tn2 =fo-tov2 [w] 1 R 2πL r 长度为L的圆筒壁的 R= 1n2 2π2Lr 导热热阻 c/w 单位长度圆筒壁的热流量: (a) Φ tw-tw2 2π入 [w/m] L In R 2π入 ,n月一单位K度剑简壁的导燕用 m.c/w] r
圆筒壁内导热热流量: W ln 2 1 1 2 1 2 1 2 R t t r r L t t Φ w w w − w = − = C W L ln 2 1 1 2 = 导热热阻 长度为 的圆筒壁的 — r r L R 单位长度圆筒壁的热流量: W m ln 2 1 1 2 1 2 1 2 l w w w w l R t t r r t t L Φ q − = − = = ln m C W 2 1 1 2 = — 单位长度圆筒壁的导热热阻 r r R l

(2)多层圆筒壁 由不同材料构成的多层圆筒壁, 其导热热流量可按总温差和总 热阻计算 tw19 Φ= twl-tw4 [w] 2 r2 twl-tw4 91= [w/m] n层圆筒壁 (a) 91= R 92 (b) i=
(2) 多层圆筒壁 由不同材料构成的多层圆筒壁, 其导热热流量可按总温差和总 热阻计算 W m ln 2 1 W ln 2 1 3 1 1 1 4 3 1 1 1 4 = + = + − = − = i i i i w w l i i i i w w r r t t q r r L t t Φ = + + = + − = − = n i i i i w wn n i li w wn l r r t t R t t q 1 1 1 1 1 1 1 ln 2 1 n 层圆筒壁
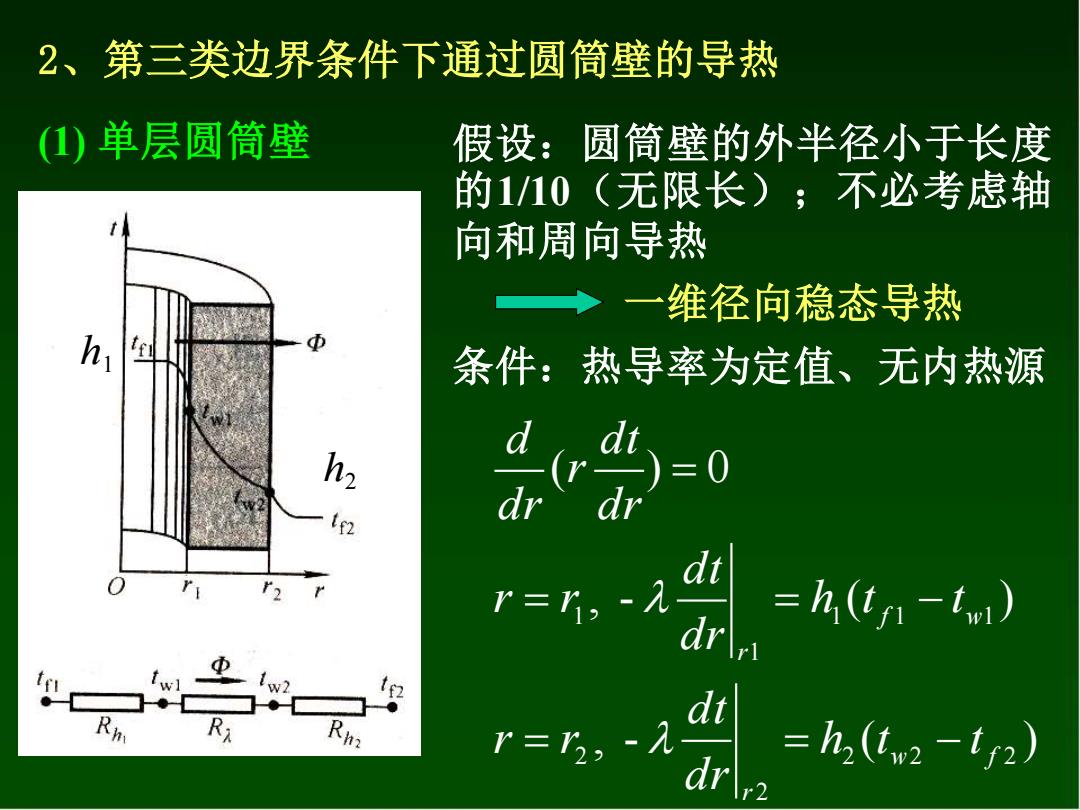
2、第三类边界条件下通过圆筒壁的导热 (1)单层圆筒壁 假设:圆筒壁的外半径小于长度 的1/10(无限长);不必考虑轴 向和周向导热 一维径向稳态导热 hy 条件:热导率为定值、无内热源 h2 =0 r=,- dr =h,(t1-tw) tw】 Rh r=5,- dt =h(tw2-t2)
一维径向稳态导热 2、第三类边界条件下通过圆筒壁的导热 (1) 单层圆筒壁 假设:圆筒壁的外半径小于长度 的1/10(无限长);不必考虑轴 向和周向导热 h1 条件:热导率为定值、无内热源 h2 , - ( ) , - ( ) ( ) 0 2 2 2 2 2 1 1 1 1 1 w f r f w r h t t d r d t r r h t t d r d t r r d r d t r d r d = = − = = − =
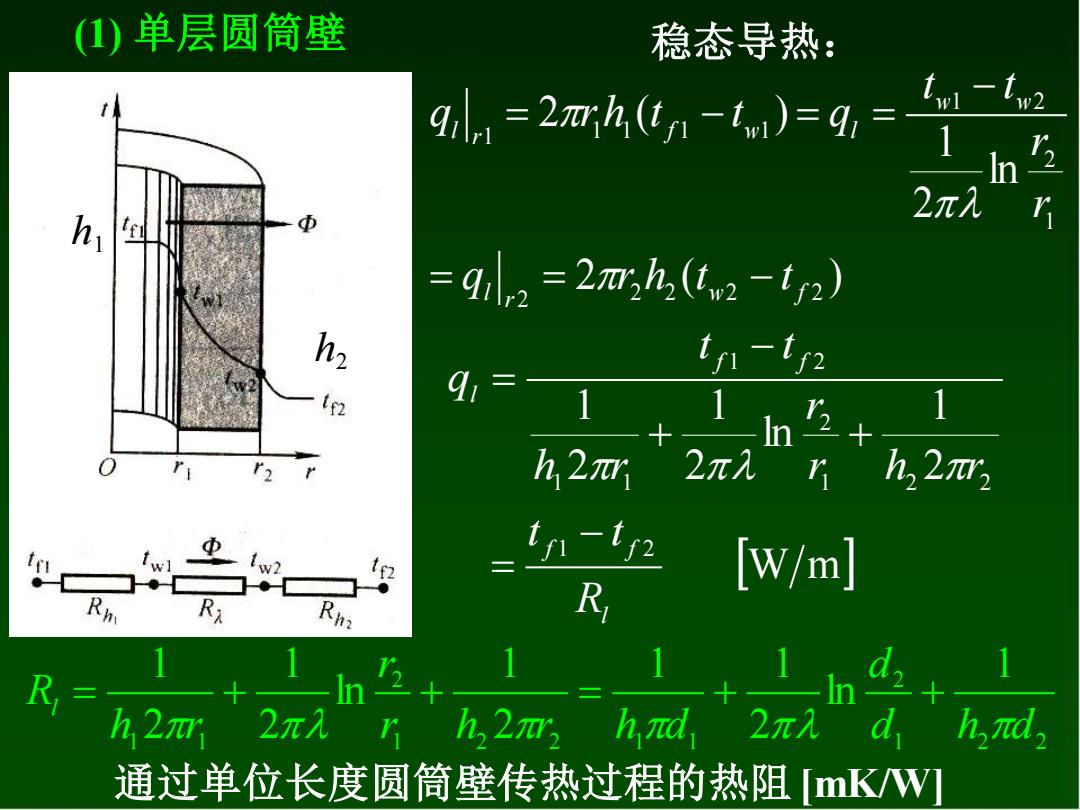
(1)单层圆筒壁 稳态导热: qn=2mh,(t1-tmi)=q,= twl -tw2 2π入 h r =ql2=2a,h,(2-t2) tn-ip 1 h2nr 2元入 万h,2π3 D fw) In-in [w/m] R R R R 2+ 1 h 2n 2π入 r h,2,had 通过单位长度圆筒壁传热过程的热阻[mKW]
(1) 单层圆筒壁 稳态导热: h1 h2 2 ( ) ln 2 1 2 ( ) 2 2 2 2 2 1 2 1 2 1 1 1 1 1 w f r l w w f w l r l q r h t t r r t t q r h t t q = = − − = − = = W m 2 1 ln 2 1 2 1 1 2 1 2 2 2 1 1 1 2 l f f f f l R t t r h r r h r t t q − = + + − = 1 ln 2 1 1 2 1 ln 2 1 2 1 1 2 2 2 1 2 2 1 1 2 1 1 d h d d r h r h d r h r Rl = + + = + + 通过单位长度圆筒壁传热过程的热阻 [mK/W]