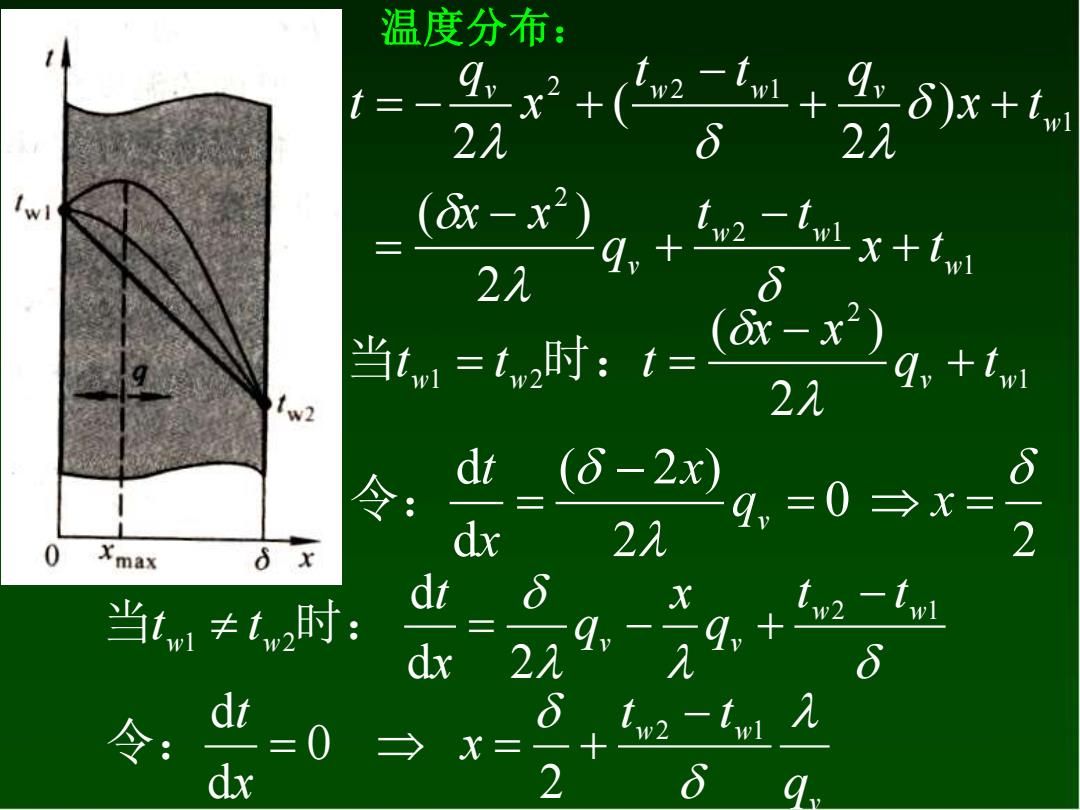
温度分布: 是++经8+ t 2 2元 (x-x2) 22 4+x+ 当=1时:t=(x-x 2入 -9y twi 令: dt (8-2x) ,=0今x= 6 0 Xmax 6 x dx 2λ 2 dt 当tn1≠t2时: 2元 g+12 令: =0 → X 2 δ
1 2 1 2 1 2 2 1 2 ( ) ) 2 ( 2 w w w v w v w w v x t t t q x x x t t t q x q t + − + − = + + − = − + 温度分布: 1 2 1 2 2 ( ) w w v w q t x x t t t + − = = 当 时: 2 0 2 ( 2 ) d d = = − = q x x x t 令: v 2 1 1 2 d 2 d w w w w v v t t q x q x t t t − 当 时: = − + v w w q t t x x t 2 1 2 0 d d − 令: = = +
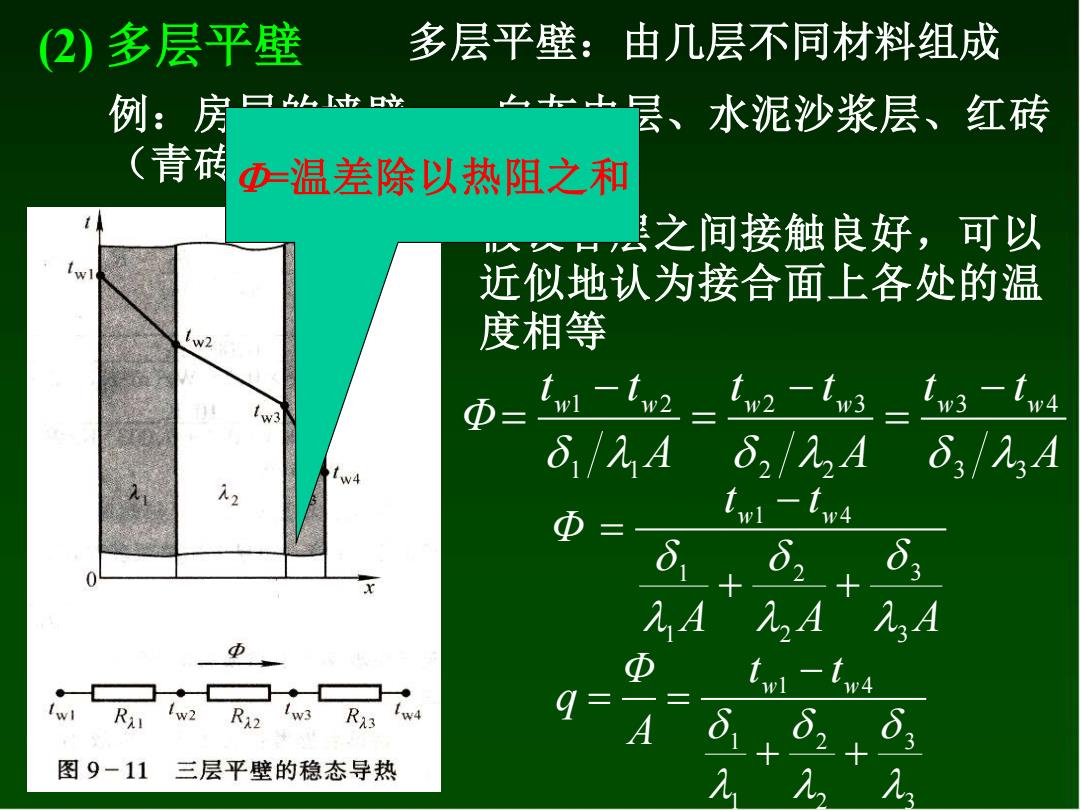
(2)多层平壁 多层平壁:由几层不同材料组成 例:房口脑 一一上层、水泥沙浆层、红砖 (青砖 Φ-温差除以热阻之和 之间接触良好,可以 近似地认为接合面上各处的温 tw2 度相等 Φ= twl -tw2 _1w2 -tw3 _tw3 -tw4 6,/2A δ2/元2A δ3/2A tl t Φ= w4 62 tw R w2 w3 图9-11三层平壁的稳态导热
(2) 多层平壁 多层平壁:由几层不同材料组成 例:房屋的墙壁 — 白灰内层、水泥沙浆层、红砖 (青砖)主体层等组成 假设各层之间接触良好,可以 近似地认为接合面上各处的温 度相等 A t t A t t A t t Φ w w w w w w 3 3 3 4 2 2 2 3 1 1 1 2 − = − = − = 3 3 2 2 1 1 1 4 A A A t t Φ w w + + − = 3 3 2 2 1 1 1 4 + + − = = w w t t A Φ q =温差除以热阻之和

对于多层(n层)平壁: Φ=乙-t1 R i=1 R2=2A
对于多层(n层)平壁: n i 1 i 1 1 = − + = R t t Φ w w n i A R i i =
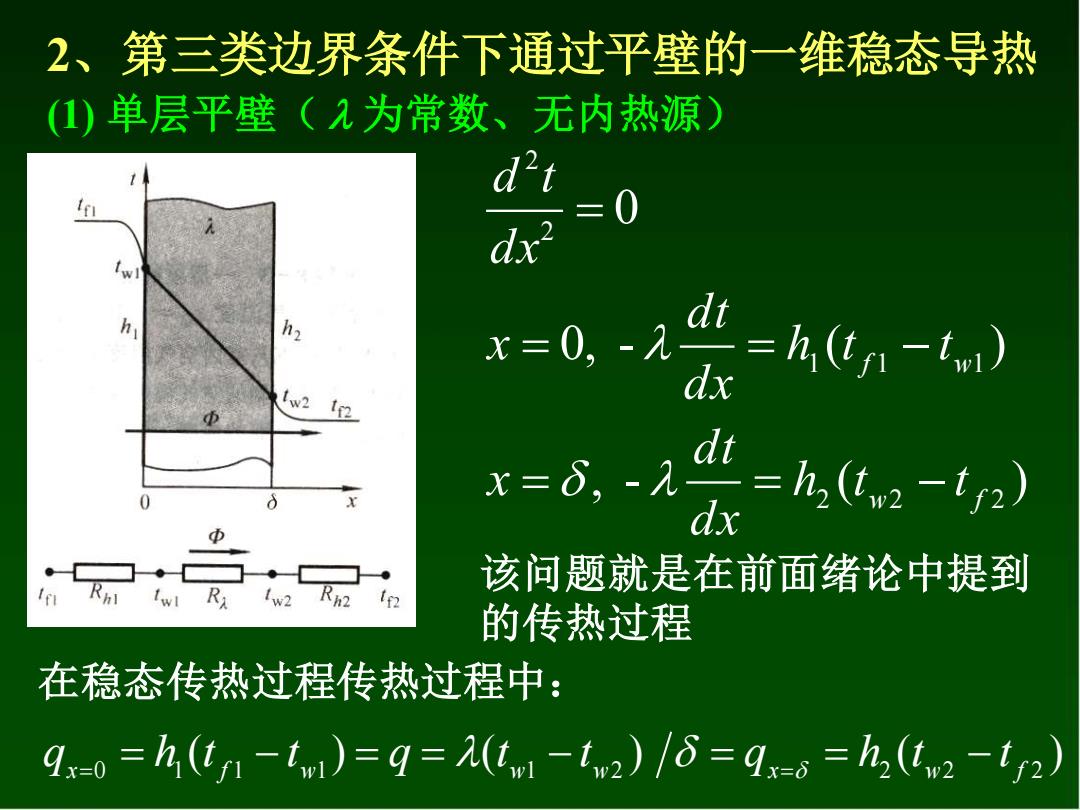
2、第三类边界条件下通过平壁的一维稳态导热 (1)单层平壁(入为常数、无内热源) d't =0 dx2 hy x=0.- dx =h,(t1-twi) w2 x=8,元4=h,-1) dx 该问题就是在前面绪论中提到 的传热过程 在稳态传热过程传热过程中: qx-0=h(t1-tw1)=q=(tm-tw2)/6=qx=5=h,(t2-tr2)
2、第三类边界条件下通过平壁的一维稳态导热 (1) 单层平壁( 为常数、无内热源) 该问题就是在前面绪论中提到 的传热过程 , - ( ) 0, - ( ) 0 2 2 2 1 1 1 2 2 w f f w h t t d x d t x h t t d x d t x d x d t = = − = = − = ( ) ( ) ( ) x 0 1 f 1 w1 w1 w2 x 2 w2 f 2 q = h t − t = q = t − t = q = h t − t = = 在稳态传热过程传热过程中:
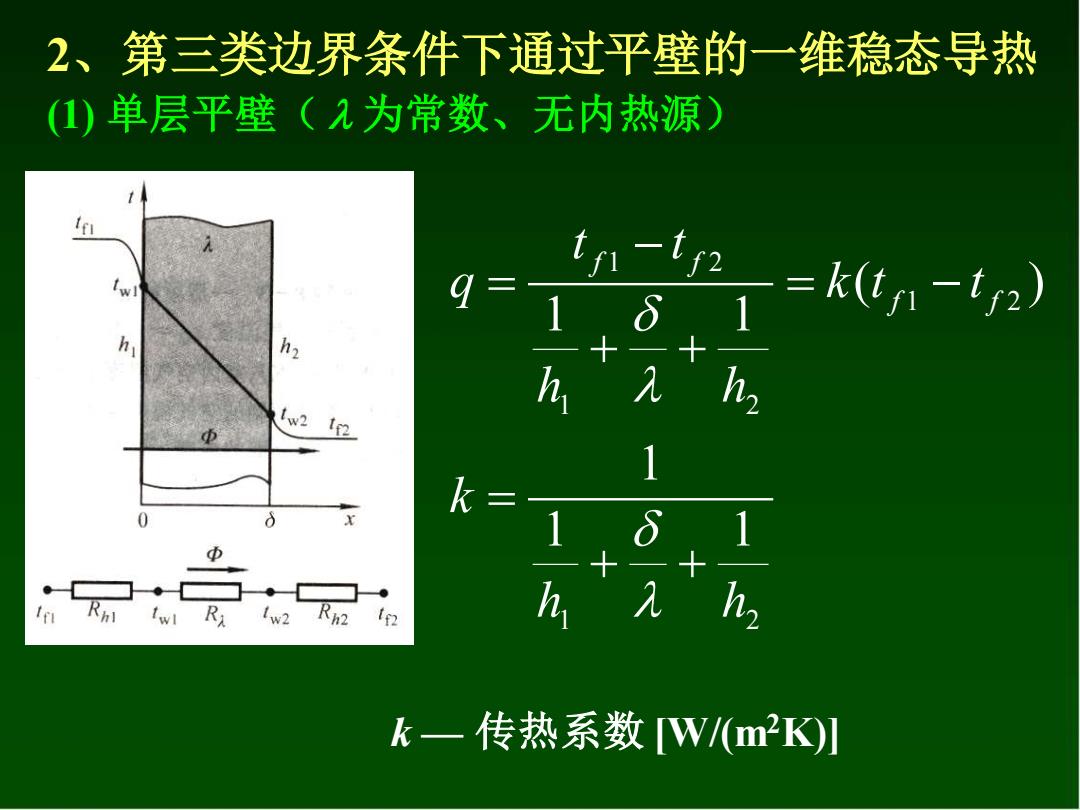
2、第三类边界条件下通过平壁的一维稳态导热 ()单层平壁(2为常数、无内热源) th -tr 1 =k(t1-ty2) h h w2 1 1 S 1 1w2 h "'h, k一传热系数W(m2K]
2、第三类边界条件下通过平壁的一维稳态导热 (1) 单层平壁( 为常数、无内热源) 1 2 1 2 1 2 1 2 1 1 1 ( ) 1 1 h h k k t t h h t t q f f f f + + = = − + + − = k — 传热系数 [W/(m2K)]