
机械与电气工程学院 School of Machanical and Elcetrical Engineering 则可得: xk =1xk-1+p2xk-2+.+mxk-M+ak+01ak-1++eNak-N 其含义是:在时刻k时的输出xk是此前M-1个输出xk-1,xk-2"Xk-M与 时刻k到k-N中N个相互独立的白噪声输入的线性和。 结论: ①当0:=0,i=1,2,…N时,有 Xk=中1Xk-1+φ2Xk-2+中MXk-M+ak M阶自回归模型AR(M) ②当:=0,1=1,2,…M时,有 Xk=ak+01xk-1+02xk-2.+eNxk-N N阶滑动平均模型MA(N) 机城与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 则可得: 𝑥𝑘 = 𝜙1𝑥𝑘−1 + 𝜙2𝑥𝑘−2 + ⋯ + 𝜙𝑀𝑥𝑘−𝑀 + 𝑎𝑘 + 𝜃1𝑎𝑘−1 + ⋯ + 𝜃𝑁𝑎𝑘−𝑁 其含义是:在时刻𝑘时的输出𝑥𝑘是此前𝑀 − 1个输出𝑥𝑘−1,𝑥𝑘−2…𝑥𝑘−𝑀与 时刻𝑘到𝑘-𝑁中𝑁个相互独立的白噪声输入的线性和。 结论: ① 当𝜃𝑖 = 0,ⅈ = 1,2, ⋯ 𝑁时,有 𝑥𝑘= 𝜙1𝑥𝑘−1 + 𝜙2𝑥𝑘−2 ⋯ + 𝜙𝑀𝑥𝑘−𝑀 + 𝑎𝑘 M阶自回归模型AR(M) ② 当𝜙𝑖 = 0,ⅈ = 1,2, ⋯ 𝑀时,有 𝑥𝑘 = 𝑎𝑘 + 𝜃1𝑥𝑘−1 + 𝜃2𝑥𝑘−2 ⋯ + 𝜃𝑁𝑥𝑘−𝑁 N阶滑动平均模型MA(N)
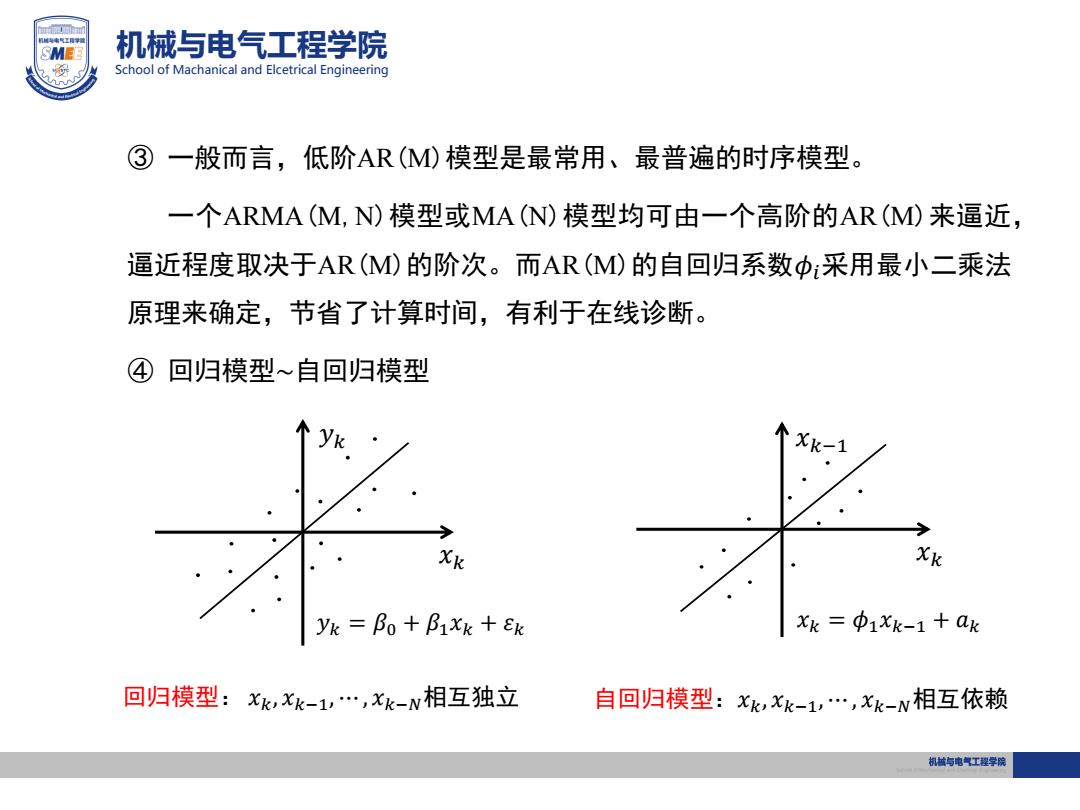
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering ③ 一般而言,低阶AR(M)模型是最常用、最普遍的时序模型。 一个ARMA(M,N)模型或MA(N)模型均可由一个高阶的AR(M)来逼近, 逼近程度取决于AR(M)的阶次。而AR(M)的自回归系数中:采用最小二乘法 原理来确定,节省了计算时间,有利于在线诊断。 ④回归模型~自回归模型 Xk- Xk XK yk =Bo Bixk +k Xk=中1Xk-1+ak 回归模型:Xk,xk-1,…,Xk-N相互独立 自回归模型:Xk,Xk-1,…,Xk-N相互依赖 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering ③ 一般而言,低阶AR(M)模型是最常用、最普遍的时序模型。 一个ARMA(M,N)模型或MA(N)模型均可由一个高阶的AR(M)来逼近, 逼近程度取决于AR(M)的阶次。而AR(M)的自回归系数𝜙𝑖采用最小二乘法 原理来确定,节省了计算时间,有利于在线诊断。 ④ 回归模型~自回归模型 𝑥𝑘 𝑦𝑘 𝑥𝑘 𝑥𝑘−1 𝑦𝑘 = 𝛽0 + 𝛽1𝑥𝑘 + 𝜀𝑘 回归模型: 𝑥𝑘, 𝑥𝑘−1, ⋯ , 𝑥𝑘−𝑁相互独立 自回归模型:𝑥𝑘, 𝑥𝑘−1, ⋯ , 𝑥𝑘−𝑁相互依赖 𝑥𝑘 = 𝜙1𝑥𝑘−1 + 𝑎𝑘