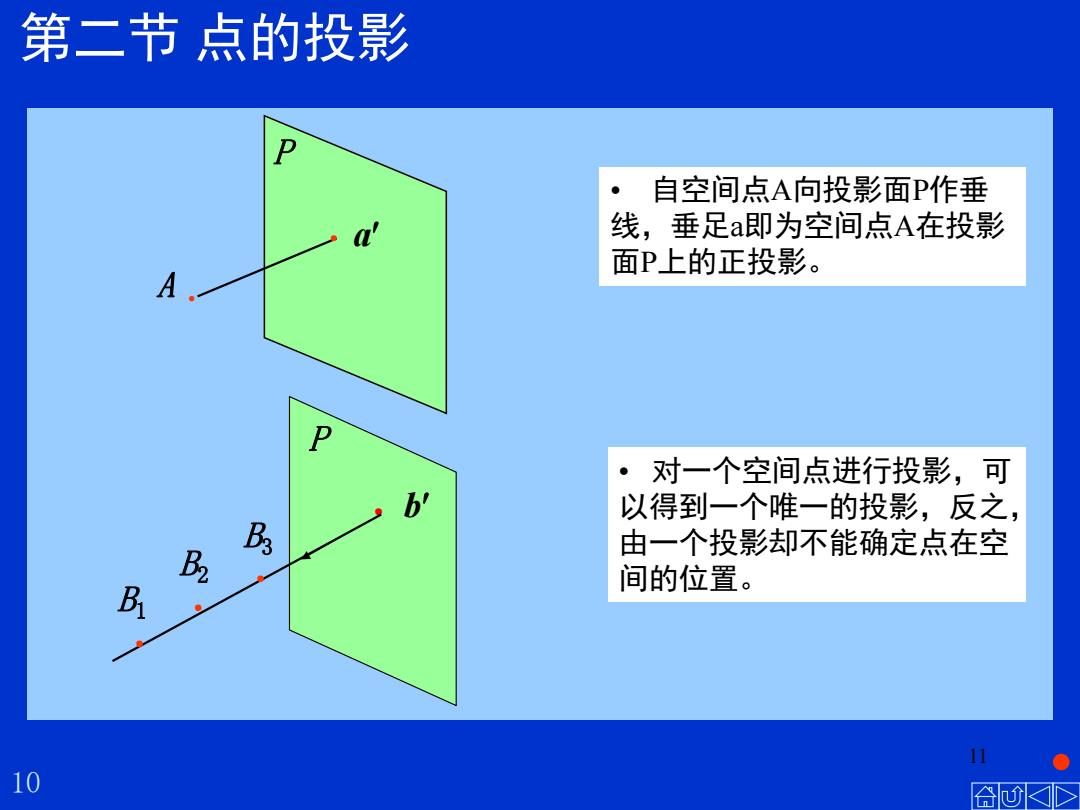
第二节点的投影 D ·自空间点A向投影面P作垂 线,垂足a即为空间点A在投影 面P上的正投影。 A ·对一个空间点进行投影,可 b 以得到一个唯一的投影,反之, 由一个投影却不能确定点在空 间的位置。 11 10
11 • 自空间点A向投影面P作垂 线,垂足a即为空间点A在投影 面P上的正投影。 • 对一个空间点进行投影,可 以得到一个唯一的投影,反之, 由一个投影却不能确定点在空 间的位置。 10 第二节 点的投影 A ● P a ● P ● b B3 B2 ● B ● 1 ●
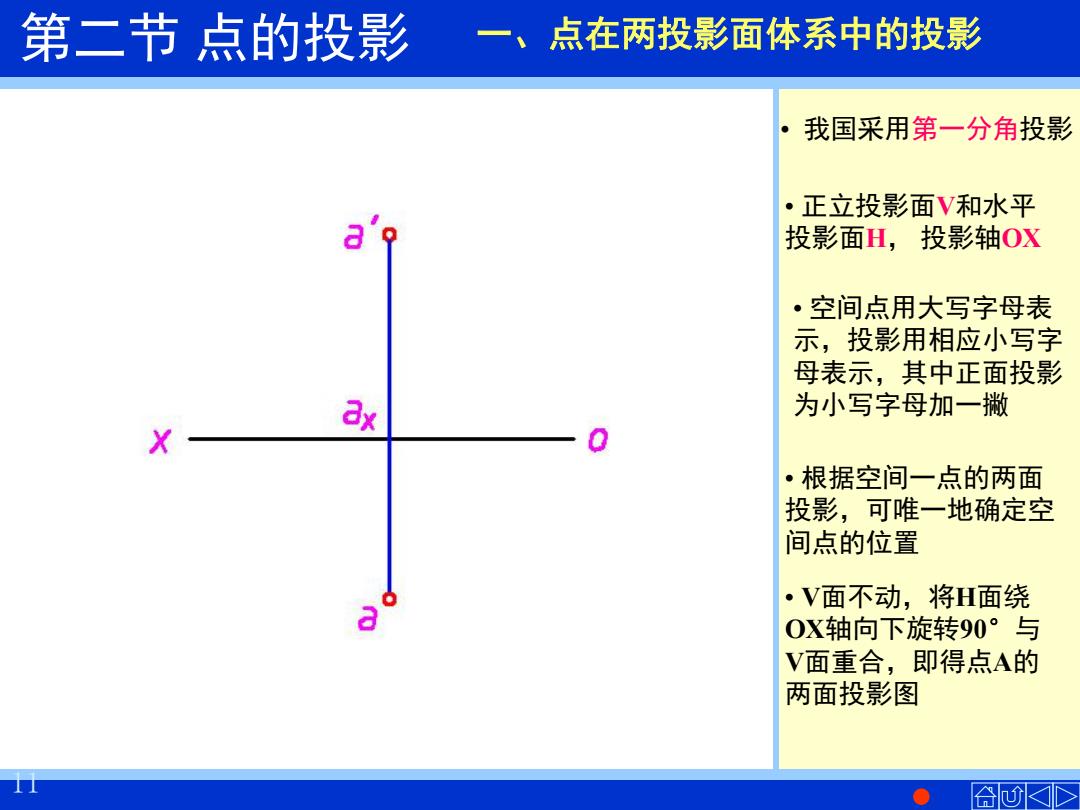
第二节点的投影 一、点在两投影面体系中的投影 。 我国采用第一分角投影 ·正立投影面V和水平 投影面H,投影轴Ox ·空间点用大写字母表 示,投影用相应小写字 母表示,其中正面投影 ax 为小写字母加一撇 X 0 ·根据空间一点的两面 投影,可唯一地确定空 间点的位置 ·V面不动,将H面绕 0X轴向下旋转90°与 V面重合,即得点A的 两面投影图 合K✉
12 一、点在两投影面体系中的投影 我国采用第一 分角投影 正立投影面V和水 平投影面H, 投影 轴OX 空间点用大写字母表示,如“A ” , 投影用相应小写字母表示,其中正面 根投据影空为间小一点写的字两母面加投一影,撇可,唯如一“地确a定’ ”空间点的位置 V面不动,将H面绕OX轴向下旋转90° 与V面重合,即得点A的两面投影图 投影面在空间可无限延伸,故无需画其边框线 用细实线画出投影轴和投影连线,并用小圆 圈表示点的投影 • 我国采用第一分角投影 • 正立投影面V和水平 投影面H, 投影轴OX • 空间点用大写字母表 示,投影用相应小写字 母表示,其中正面投影 为小写字母加一撇 • 根据空间一点的两面 投影,可唯一地确定空 间点的位置 • V面不动,将H面绕 OX轴向下旋转90°与 V面重合,即得点A的 两面投影图 11 第二节 点的投影
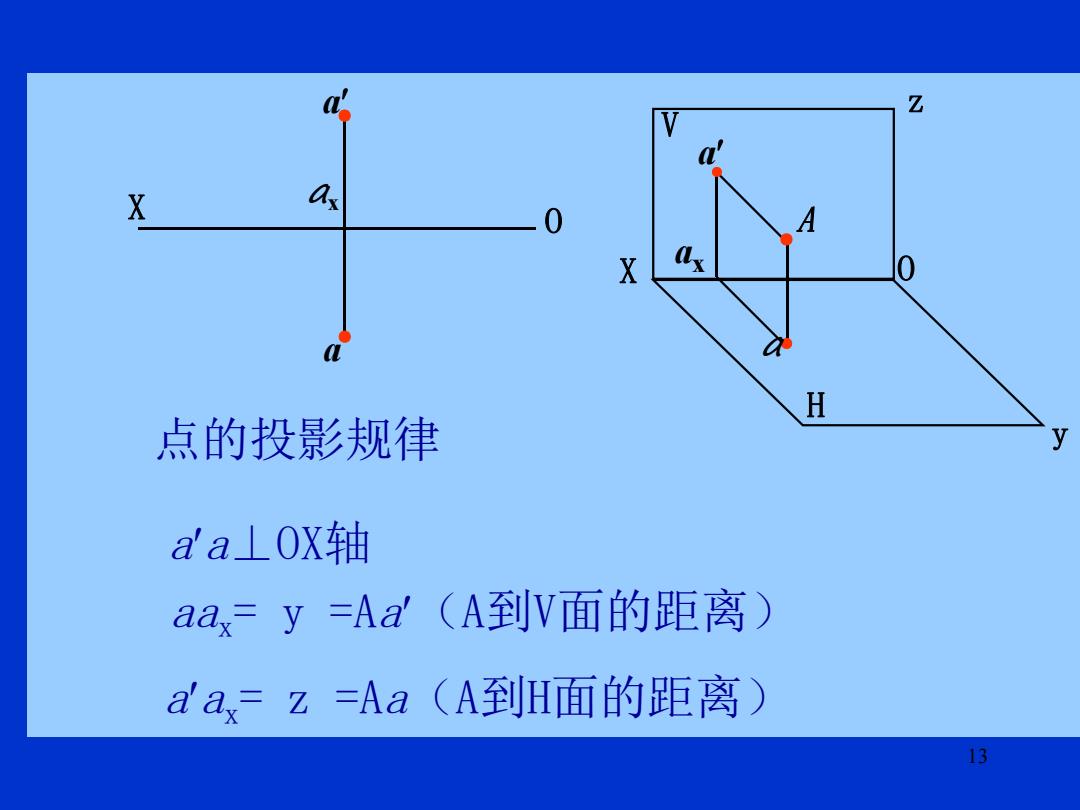
Z X as 0 A X 4 0 H 点的投影规律 y aa⊥OX轴 aax=y=Aa(A到V面的距离) aax=z=Aa(A到H面的距离) 13
13 ● ● ● X O V H A a a aa⊥OX轴 x a aax = y =Aa(A到V面的距离) aax = z =Aa(A到H面的距离) X ● a ax a ● O 点的投影规律 z y
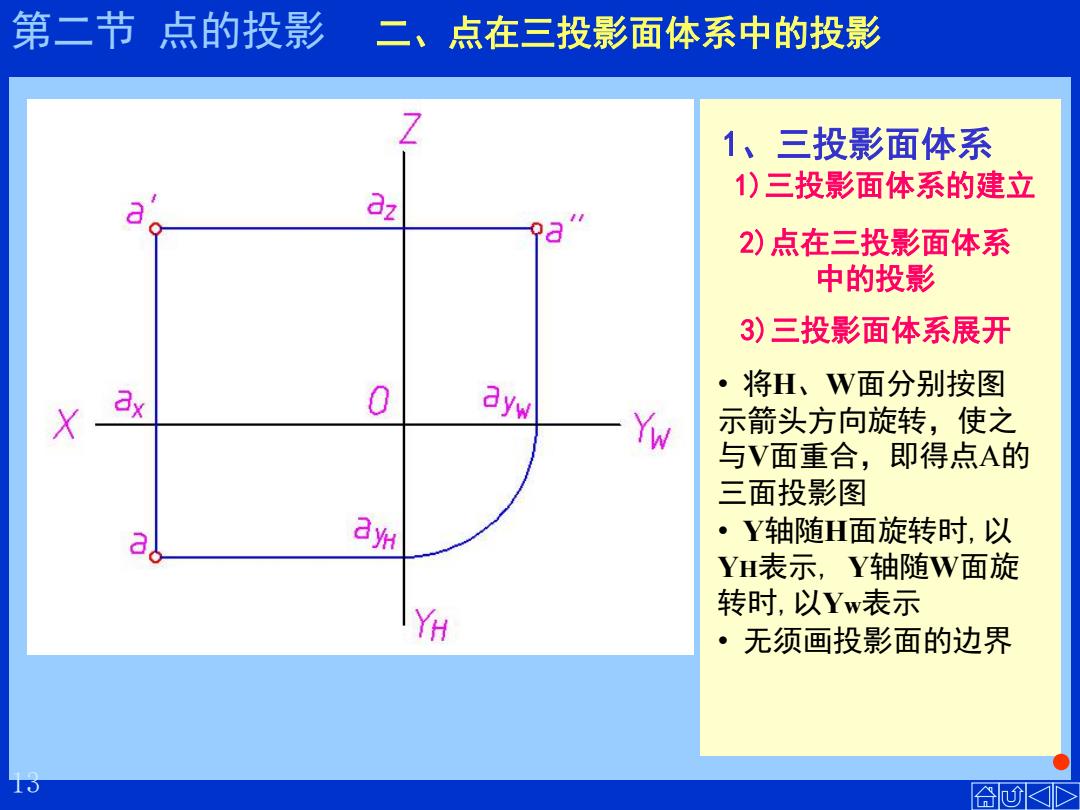
第二节点的投影二、点在三投影面体系中的投影 Z 1、三投影面体系 1)三投影面体系的建立 az 2)点在三投影面体系 中的投影 3)三投影面体系展开 。 X x 0 ayw 将H、W面分别按图 Yw 示箭头方向旋转,使之 与V面重合,即得点A的 三面投影图 a ay州 ·Y轴随H面旋转时,以 YH表示,Y轴随W面旋 YH 转时,以Yw表示 ·无须画投影面的边界 合
14 第二节 点的投影 1)三投影面体系的建立 • 在两投影面体系上再 加上一个与V、H均垂 直的侧立投影面W,三 个互相垂直的H、V、 W面组成一个三投影面 体系 • 投影轴:OX、OY、 OZ • 三轴交点:原点O 2)点在三投影面体系 中的投影 • 空间点A,分别向V、 H、W面投影得a、a’ 、a” ,其中a”是点A的侧面 投影 3)三投影面体系展开 • 将H、W面分别按图 示箭头方向旋转,使之 与V面重合,即得点A的 三面投影图 • 无须画投影面的边界 • Y轴随H面旋转时,以 YH表示, Y轴随W面旋 转时,以Yw表示 1、三投影面体系 二、点在三投影面体系中的投影 13
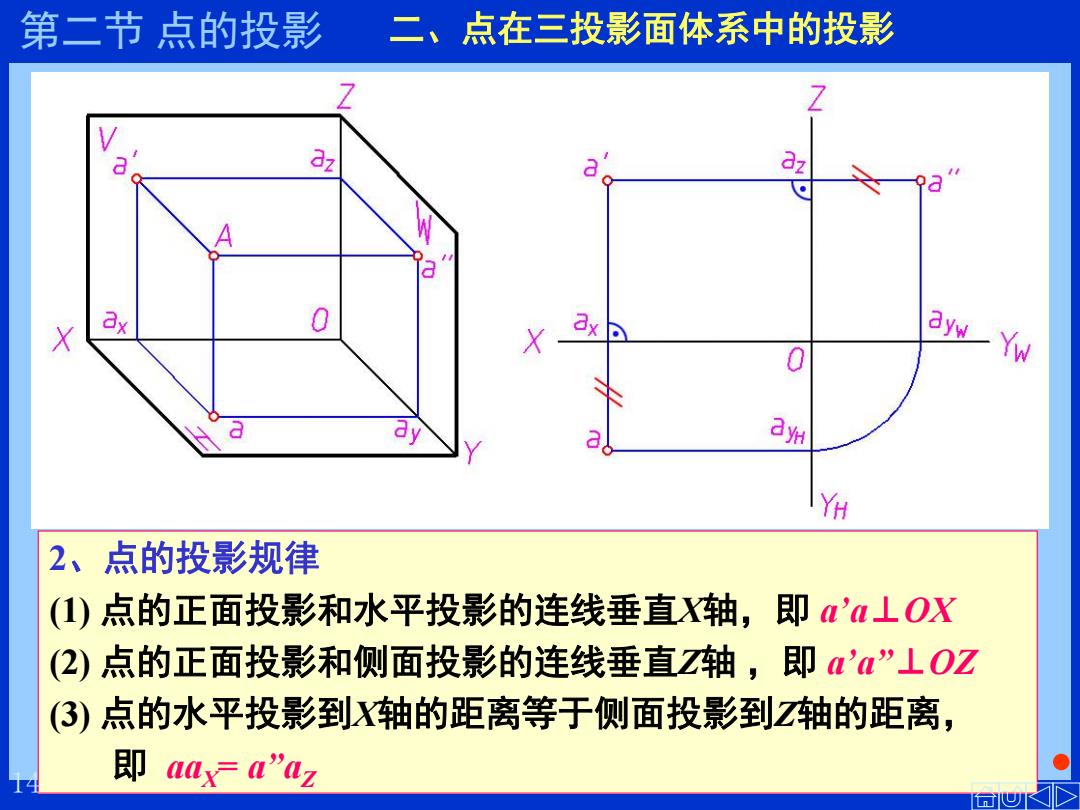
第二节点的投影 二、点在三投影面体系中的投影 Z a dz a ax 0 X X ax aywYw a ay a州 YH 2、点的投影规律 (1)点的正面投影和水平投影的连线垂直X轴,即a'a⊥OX (2)点的正面投影和侧面投影的连线垂直Z轴,即a'a”⊥OZ (3)点的水平投影到X轴的距离等于侧面投影到Z轴的距离, 即aa=a”'az
15 2、点的投影规律 (1) 点的正面投影和水平投影的连线垂直X轴,即 a’a⊥OX (2) 点的正面投影和侧面投影的连线垂直Z轴 ,即 a’a”⊥OZ (3) 点的水平投影到X轴的距离等于侧面投影到Z轴的距离, 即 aaX = a”aZ 二、点在三投影面体系中的投影 14 第二节 点的投影