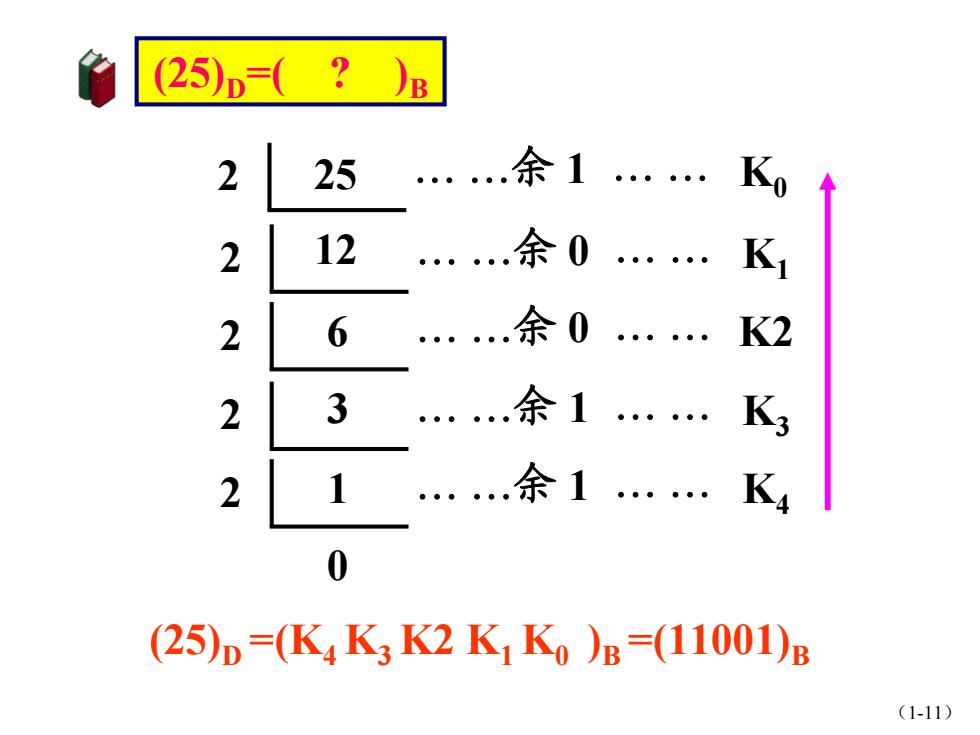
(25)D=( B 2 25 余1.K0 2 12 余0.K1 2 6 余0.K2 2 3 余1.K3 2 1 .余1. K 0 (25)D=(K4K3K2K,K)B=(11001)B (1-11)
(1-11) 2 25 余 1 K0 2 12 余 0 K1 2 6 余 0 K2 2 3 余 1 K3 2 1 余 1 K4 0 (25)D =(K4 K3 K2 K1 K0 )B =(11001)B (25)D =( ? )B

(2695)n=(?) =(A87)u 162695 余.7 16 168 余.8 16 10 余A 0 5.十进制(小数)转换为二进制数 转换方法:将十进制小数乘以2,取其个位 整数,直到满足误差要求进行“四舍五入”为止, 例 P17的例1.3.5 (1-12)
(1-12) (2695)D =( ? )H 1 6 2 6 9 5 余 7 1 6 1 6 8 余 8 1 0 0 1 6 余 A 5. 十进制(小数)转换为二进制数 =(A 8 7)H 转换方法:将十进制小数乘以2 , 取其个位 整数 , 直到满足误差要求进行“四舍五入”为止. 例 P17的例1.3.5
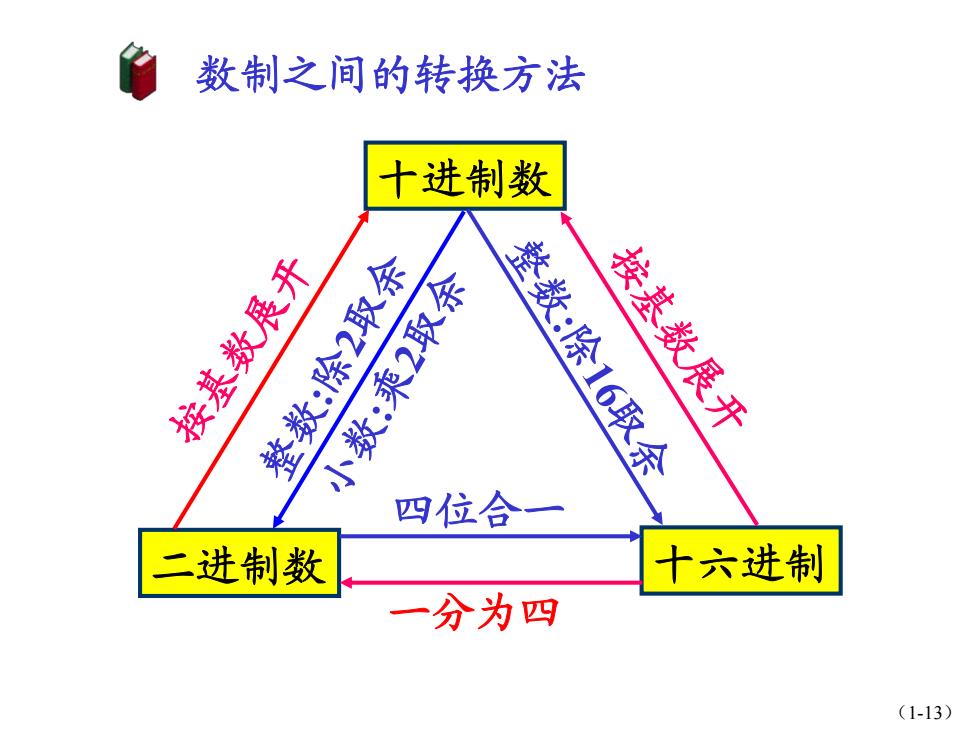
数制之间的转换方法 十进制数 整数:除2取余 按基数展开 小数:乘2取余 整数:除16取余 按基数展开 四位合 二进制数 十六进制 一分为四 (1-13)
(1-13) 十进制数 二进制数 十六进制 按基数展开 按基数展开 整数:除16取余 四位合一 一分为四 数制之间的转换方法 整数:除2取余 小数:乘2取余

1.2二进制数的算术运算(arithmetic) ◆Addition Augend +addend +carry-in Sum .carry-out ◆Subtraction -Minuend-subtrahend-borrow-in difference .borrow-out ◆Division -Dividend divisor quotient .remainder ◆ultiplication Multiplicand multiplier product (1-14)
(1-14) ◆Addition – Augend +addend +carry-in = Sum .carry-out ◆ Subtraction – Minuend – subtrahend – borrow-in = difference .borrow-out 1.2 二进制数的算术运算(arithmetic) arithmetic) ◆ Division – Dividend / divisor = quotient . remainder ◆ Multiplication – Multiplicand * multiplier = product