
导航 常用方法 规律特点 平均 v- ,对任何性质的运动都适用; 速度法 7=w+,只适用于匀变速直线运动 中间时刻 速度法 V:=7=w+),适用于匀变速直线运动 对于初速度为零的匀加速直线运动或末速度为零的 比例法 匀减速直线运动,可利用比例法求解
导航 常用方法 规律特点 平均 速度法 𝐯 = 𝐱 𝐭 ,对任何性质的运动都适用; 𝐯 = 𝟏 𝟐 (v0+v),只适用于匀变速直线运动 中间时刻 速度法 𝐯𝐭 𝟐 = 𝐯 = 𝟏 𝟐 (v0+v),适用于匀变速直线运动 比例法 对于初速度为零的匀加速直线运动或末速度为零的 匀减速直线运动,可利用比例法求解

导 常用方法 规律特点 把运动过程的“末态”作为“初态”,使运动反向的方 逆向 法。例如,末速度为零的匀减速直线运动可以看作 思维法 反向的初速度为零的匀加速直线运动 应用-图像,可把复杂的物理问题转化为较为简单 图像法 的数学问题解决,尤其是用图像定性分析,可避免繁 杂的计算,快速求解
导航 常用方法 规律特点 逆向 思维法 把运动过程的“末态”作为“初态”,使运动反向的方 法。例如,末速度为零的匀减速直线运动可以看作 反向的初速度为零的匀加速直线运动 图像法 应用v-t图像,可把复杂的物理问题转化为较为简单 的数学问题解决,尤其是用图像定性分析,可避免繁 杂的计算,快速求解
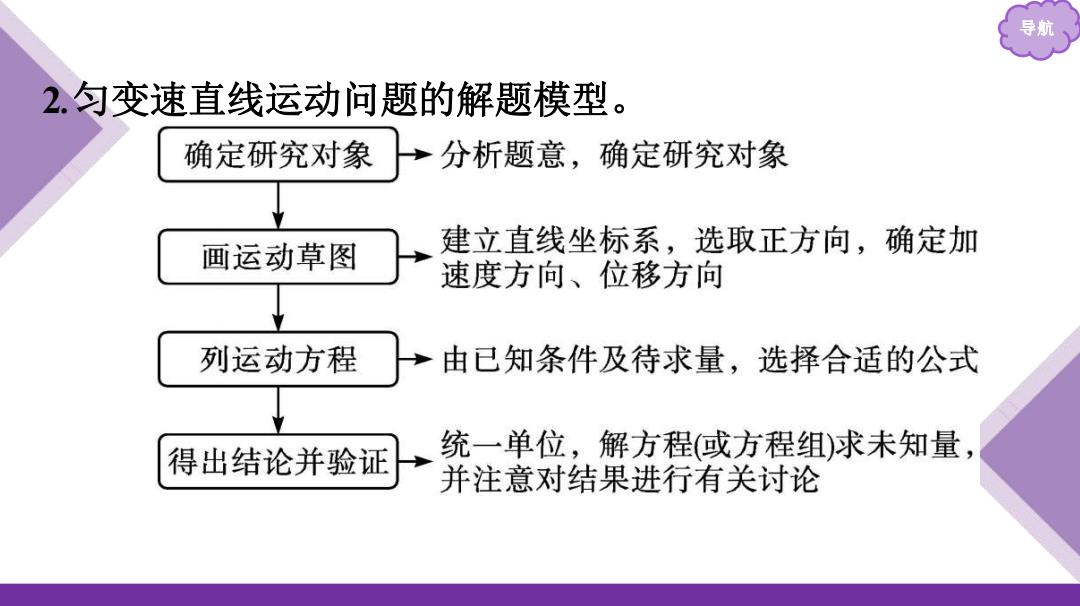
导航 2.匀变速直线运动问题的解题模型。 确定研究对象 →分析题意,确定研究对象 画运动草图 建立直线坐标系,选取正方向,确定加 速度方向、位移方向 列运动方程 由已知条件及待求量,选择合适的公式 得出结论并验证 统一单位,解方程(或方程组)求未知量 并注意对结果进行有关讨论
导航 2.匀变速直线运动问题的解题模型

【典型例题1】在平直的测试汽车加速性能的场地上,每隔 100有一个醒目的标志杆,两名测试员驾车由某个标志杆静 止开始匀加速启动,当汽车通过第二个标志杆开始计时,=10 s时,恰好经过第5个标志杆,,=20s时,恰好经过第10个标志杆, 汽车运动过程中可视为质点,如图所示。 ()求汽车的加速度大小。 23456 (2)若汽车匀加速达到最大速度 64m/s后立即保持该速度匀速 行驶,则汽车从20s末到30s末经过几个标志杆? 答案:(1)2m/s2(2)6个
导航 【典型例题1】在平直的测试汽车加速性能的场地上,每隔 100 m有一个醒目的标志杆,两名测试员驾车由某个标志杆静 止开始匀加速启动,当汽车通过第二个标志杆开始计时,t1 =10 s时,恰好经过第5个标志杆,t2 =20 s时,恰好经过第10个标志杆, 汽车运动过程中可视为质点,如图所示。 (1)求汽车的加速度大小。 (2)若汽车匀加速达到最大速度 64 m/s后立即保持该速度匀速 行驶,则汽车从20 s末到30 s末经过几个标志杆? 答案:(1) 2 m/s2 (2)6个

导 解析:()设汽车的加速度为,经过第二个标志杆的速度为。 在0-10s内有3ewf+号at12 在0~20s内有8=w+2at22 解得=2m/s2。 (2)由(1)解得v=20m/s 第20s时v=y+t2=60m/s 到达最大速度y'=叶△t 代入数据得△2s t3=30s
导航 解析:(1)设汽车的加速度为a,经过第二个标志杆的速度为v0。 在 0~10 s 内有 3l=v0t1+ 𝟏 𝟐 𝒂𝒕 𝟏 𝟐 在 0~20 s 内有 8l=v0t2+ 𝟏 𝟐 𝒂𝒕 𝟐 𝟐 解得a=2 m/s2 。 (2)由(1)解得v0 =20 m/s 第20 s时v=v0+at2 =60 m/s 到达最大速度v'=v+aΔt 代入数据得Δt=2 s t3 =30 s