2.电子导电:金属 这样的模型实际上类似量子 力学中的“一维无限深方势 阱” 2 nπx p(x)= n2π2h2 En=2mL2 =1 但是由此引出一个问题: 这样一来,波函数是以材料表面为边界的“驻波”,而“行波”才能 更好的研究电子传输行为 "God made the bulk,the surface was invented by the devil." Wolfgang Pauli
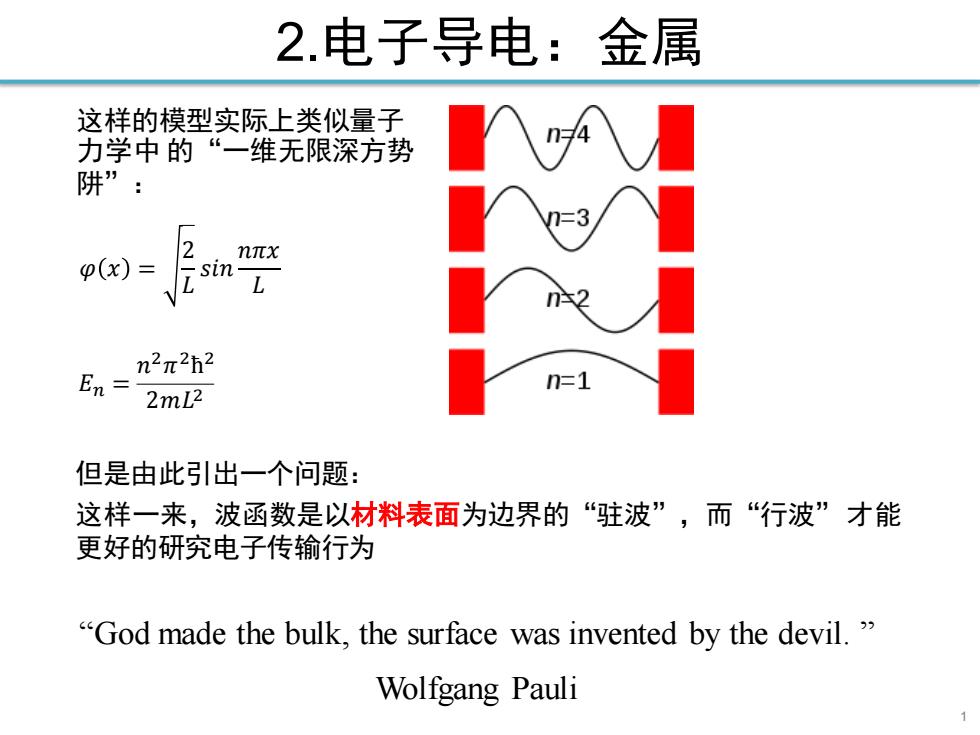
1 2.电子导电:金属 这样的模型实际上类似量子 力学中 的“一维无限深方势 阱”: 𝜑 𝑥 = 2 𝐿 𝑠𝑖𝑛 𝑛𝜋𝑥 𝐿 𝐸𝑛 = 𝑛 2𝜋 2ħ 2 2𝑚𝐿 2 但是由此引出一个问题: 这样一来,波函数是以材料表面为边界的“驻波”,而“行波”才能 更好的研究电子传输行为 “God made the bulk, the surface was invented by the devil. ” Wolfgang Pauli

2.电子导电:金属 Sommerfield模型中回避表面问题的方式:“起点即终点” 0(化,乃+L)=p化,)
2 2.电子导电:金属 Sommerfield模型中回避表面问题的方式:“起点即终点” 对于一维空间,相当于让直线闭合成圆环: 表面 材料内部 表面 L 周长L 表面重合 边界条件: x [0, L]时(x) = 0 (x+L) = (x) 将这一边界条件拓展到三维空间,就是所谓的Born-von Karman条件 (x+L, y, z) = (x, y, z) (x, y+L, z) = (x, y, z) (x, y, z+L) = (x, y, z)

2.电子导电:金属 h2 72φ()=Ep() 2m 通过代入法可以验证,薛定谔方程的解(无论是否考虑边界条件) 和对应的能量E具备以下形式: pk()= 4= 2m 其中是一个量子化的矢量,可以被理解为代表电子的物质波的波矢 因此,根据动量、能量、波长间的关系,容易得出k和波长入以及动量 有以下关系 市=hk 2π
3 2.电子导电:金属 − ħ 2 2𝑚 𝛻 2 𝑟 Ԧ = 𝐸 𝑟 Ԧ 通过代入法可以验证,薛定谔方程的解(无论是否考虑边界条件) 和对应的能量E具备以下形式: 𝜑𝑘 𝑟 Ԧ = 1 𝑉 𝑒 𝑖𝑘∙𝑟Ԧ 𝐸𝑘 = ħ 2 𝑘 2 2𝑚 其中𝑘是一个量子化的矢量,可以被理解为代表电子的物质波的波矢 因此,根据动量、能量、波长间的关系,容易得出𝑘和波长 以及动量p 有以下关系 = 2𝜋 𝑘 𝑝 Ԧ = ħ𝑘

2.电子导电:金属 由于薛定谔方程的解pk()需要服从Born-von Karman条件: p(x+L,y.z=p(x,y.2) 0(x,y+L,2)=p(x,y2) o(x,y,z+L=(x,y2 将p()=eif代入以上三个边界条件后,很容易得到 eikxl =eikyl eikzl =1 (kk,k为k在x,y方向上的分量) nx,n,n可以取任意整数
4 2.电子导电:金属 由于薛定谔方程的解𝜑𝑘 𝑟 Ԧ 需要服从Born-von Karman条件: (x+L, y, z) = (x, y, z) (x, y+L, z) = (x, y, z) (x, y, z+L) = (x, y, z) 将𝜑𝑘 𝑟 Ԧ = 1 𝑉 𝑒 𝑖𝑘∙𝑟Ԧ代入以上三个边界条件后,很容易得到 𝑒 𝑖𝑘𝑥𝐿 = 𝑒 𝑖𝑘𝑦𝐿 = 𝑒 𝑖𝑘𝑧𝐿 = 1 (kx , ky , kz为𝑘在x, y, z方向上的分量) 𝑘𝑥 = 2𝜋𝑛𝑥 𝐿 , 𝑘𝑦 = 2𝜋𝑛𝑦 𝐿 , 𝑘𝑧 = 2𝜋𝑛𝑧 𝐿 nx , ny , nz可以取任意整数

2.电子导电:金属 波矢分布密度(描述k空间中单位体积包含的状态数) 在波矢量飞,飞,飞,构成的空间(k空间,动量空间)中每一个点 表示一个(n,n,n),代表一个状态。每个状态占据的体积为(2πL)3。 k空间单位体积所含点数: (2πL)3=18元=p 由于每个波矢可以容纳自旋相反的两个电子,在体积元d之中可容 纳的电子状态数为 dZ 2p(k)dk dk ky 二维: 三维: 每个点对应一个电子 k空间中电子 k波失,每个波失占据 态所对应的等 k空间(2π/L)2的面积, 能面为球形。 以原点为圆心的圆形 上每一点能量相同
5 2.电子导电:金属 波矢分布密度(描述k空间中单位体积包含的状态数) 二维: 每个点对应一个电子 波失,每个波失占据 k 空间(2π/L)2的面积, 以原点为圆心的圆形 上每一点能量相同。 三维: k空间中电子 态所对应的等 能面为球形。 状态数为