
2.电子导电:金属 电子的能级密度(描述单位能量范围内容纳的电子数) 如果以NE)表示能量低于或等于E的电子态的数量 那么Z(E)=dWdE-能级E的态密度(Density of States,DOS) 波矢k的电子能量为E(k)= k2 2m 2m 在能量为E的球体中,波矢k的取值总数为 N=2p(k)3ks p=/8π3 k=√2mE/方 态密度Z(E)为 PDOS gl/2 Z(E)=dN/dE C√E C= V(2m 3/2 PDOS 2m2方2 E=const. 不同维度DOS与E关系 3D:E12 2D:常数 DOS 1D:~E1/2 x6-1/2 E
𝑁 = 2𝜌(𝒌) 4 3 𝜋𝒌 3 6 2.电子导电:金属 电子的能级密度(描述单位能量范围内容纳的电子数) 如果以N(E) 表示能量低于或等于E的电子态的数量 那么Z(E) = dN/dE = 能级E的态密度(Density of States, DOS)

2.电子导电:金属 根据Pui不相容原理,每个量子态(即每个)只能被两个自旋相反的电 子占据。 因此,在基态(T=0K),电子结构可以这样确定:将电子逐个填入未被 占据的能量最低的电子态中,直到N个电子都“各得其所”。 如果N足够大,那么被占据的轨道在k空间中看来将接近一个球形。它的球 面称为费米面,其半径称为费米波矢kF,能量称为费米能量E,Ek称为 费米温度T 关于费米能量E更严格的定义: 费米面 0K时金属基态系统电子所占有的能 级最高的能量
7 2.电子导电:金属 根据Pauli不相容原理,每个量子态(即每个𝑘)只能被两个自旋相反的电 子占据。 因此,在基态(T = 0 K),电子结构可以这样确定:将电子逐个填入未被 占据的能量最低的电子态中,直到N个电子都“各得其所”。 如果N足够大,那么被占据的轨道在k空间中看来将接近一个球形。它的球 面称为费米面,其半径称为费米波矢𝑘𝐹,能量称为费米能量EF,EF /kB称为 费米温度TF。 关于费米能量EF更严格的定义: 0K时金属基态系统电子所占有的能 级最高的能量 费米面
2.电子导电:金属 更普遍的,如果也考虑T>OK的情况,电子将遵从Fermi-Dirac分布: 金属中具有能量E的状态被电子占据的几率是 f(E)= 1+exp E-Er E) T>OK 1.0 T=0K 0.5- 0 E E
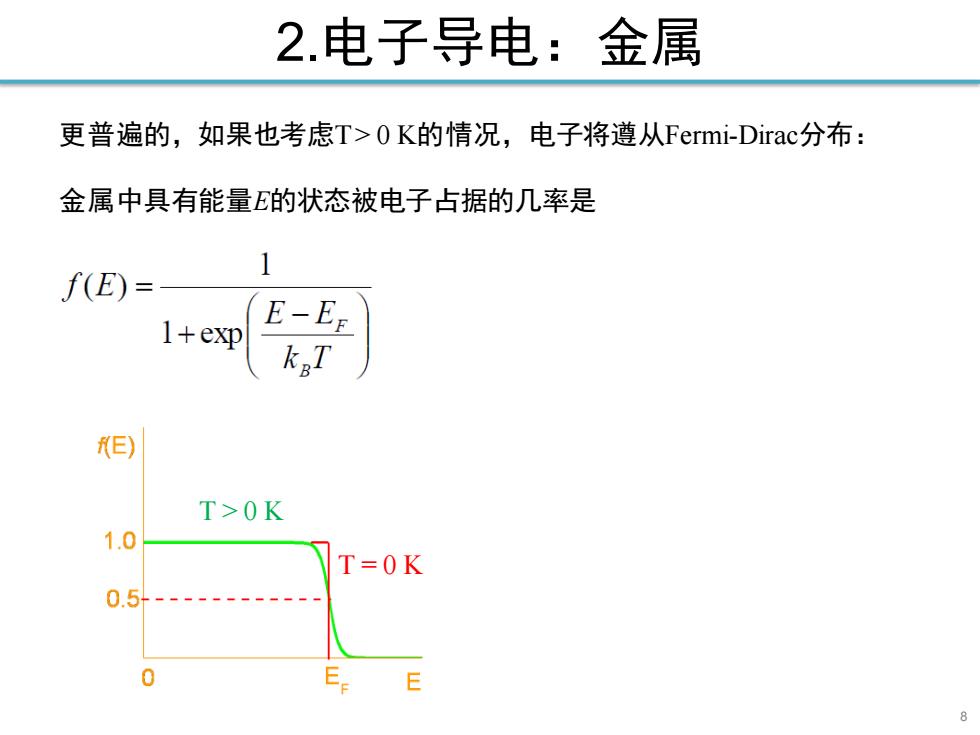
8 2.电子导电:金属 更普遍的,如果也考虑T > 0 K的情况,电子将遵从Fermi-Dirac分布: 金属中具有能量E的状态被电子占据的几率是 T > 0 K T = 0 K