
18 v=cT有()=C=兰 代入上式后得 dW=-dp+¥dr或y=-2+ 上式积分得 lnV+lnp=lnT+常数 若所取气体的量是1mol,则体积写作Vm,常数写作R,即得 pV=RT 上式两边同乘以物质的量n,则得 pV nRT 这就是理想气体的状态方程式。已知m=,N是分子的个数,L是Avogadro 常数。令:尽=k,ks称为Boltzmann(玻耳兹曼)常数,则上式又可写作: PV NknT (1.15) 5.Dalton分压定律 若在定温下,把几种不同的气体混合于容积为V的容器中,各种分子的数 目分别为,N2,.,总分子数为N,十N2十.=N。混合气体可设想是通过 如下的混合过程来完成, T.V T.V T.V N:P N:.P: N,N2,N. 混合前, A=N,m时=号YE A:=N:m:暖=号兰E 诸式相加 ∑p,=[N,E+N,E+.] 混合后, p=3是NmE

文雪11气体分子动理论19 由于相同温度下,各气体分子具有相同的平均动能,即 E=E=.=E Nmx=N,+N2+. 所以 p=p1十p十. (1.16 这就是Dalton分压定律(Dalton's law of partial pressure),即混合气体的 总压等于各气体分压之和。所谓分压,就是在同一温度下,各别气体单独存在、 并占有与混合气体相同体积时所具有的压力。 若任一种气体的分压除以总压,则得 N 式中x,是摩尔分数。这是Dalton分压定律的另一种形式。 6.Amagat(阿马格)分体积定律 在一定的T,p时,混合气体的体积等于组成该混合气体的各组分的分体积 之和,即 V=V1+V2+. 这就是Amagat分体积定律(Amagat's law of partial volume),所谓某一组 分的体积,它等于该气体在温度T和总压p时单独存在时所占据的体积。 设有两种气体的混合过程如下图所示, V, T.D.N T.p.N:T.p.(N:+N,) V:=V:+V, 由此并可导出 V,=Vri (1.17) 根据气体的运动公式,不难导出Amagat分体积定律(读者试自证之)。 由式(1.17)可知,在混合气体中各气体的体积分数就等于它的摩尔分数 (在工业分析中经常使用的气体分析仪,就使用了这一定律) 分子平均平动能与温度的关系 已知气体分子的平均平动能是温度的函数,即
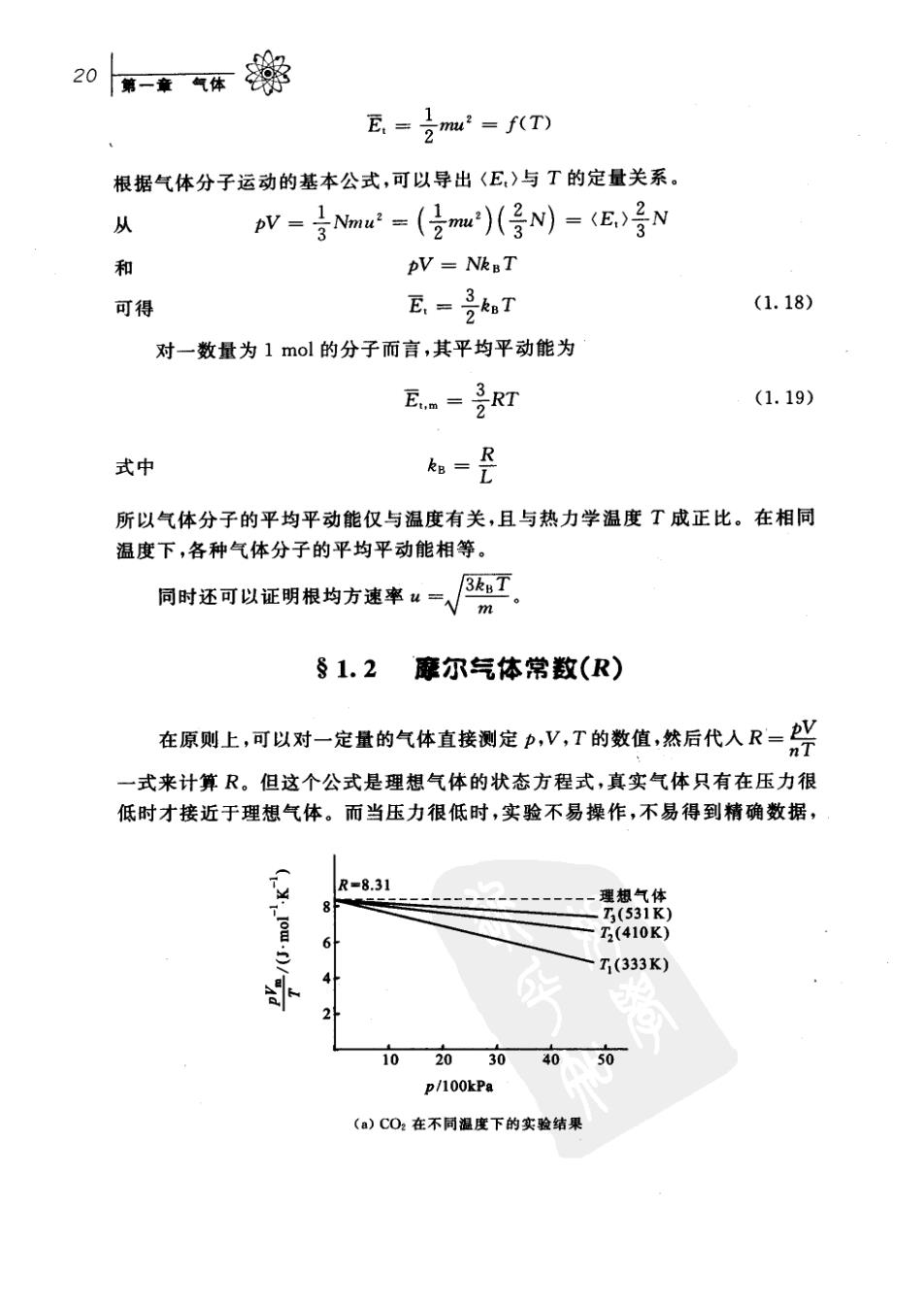
20=来气车黎 E=之mu2=fTD 根据气体分子运动的基本公式,可以导出〈E)与T的定量关系。 pV=号ma2=(2m)(号N))-(E,)号N 袋 pV NknT 可得 E,=子aT (1.18) 对一数量为1mol的分子而言,其平均平动能为 E=是RT (1.19) 式中 如= 所以气体分子的平均平动能仅与温度有关,且与热力学温度T成正比。在相同 温度下,各种气体分子的平均平动能相等。 同时还可以证男根均方速率:=√ §1.2摩尔气体常数(R) 在原则上,可以对一定量的气体直接测定,V,T的数值,然后代人R-光 一式来计算R。但这个公式是理想气体的状态方程式,真实气体只有在压力很 低时才接近于理想气体。而当压力很低时,实验不易操作,不易得到精确数据, R-831 T7(410K) 7(333K) 102030 4050 p/100kPa (a)C02在不同温度下的实验结果
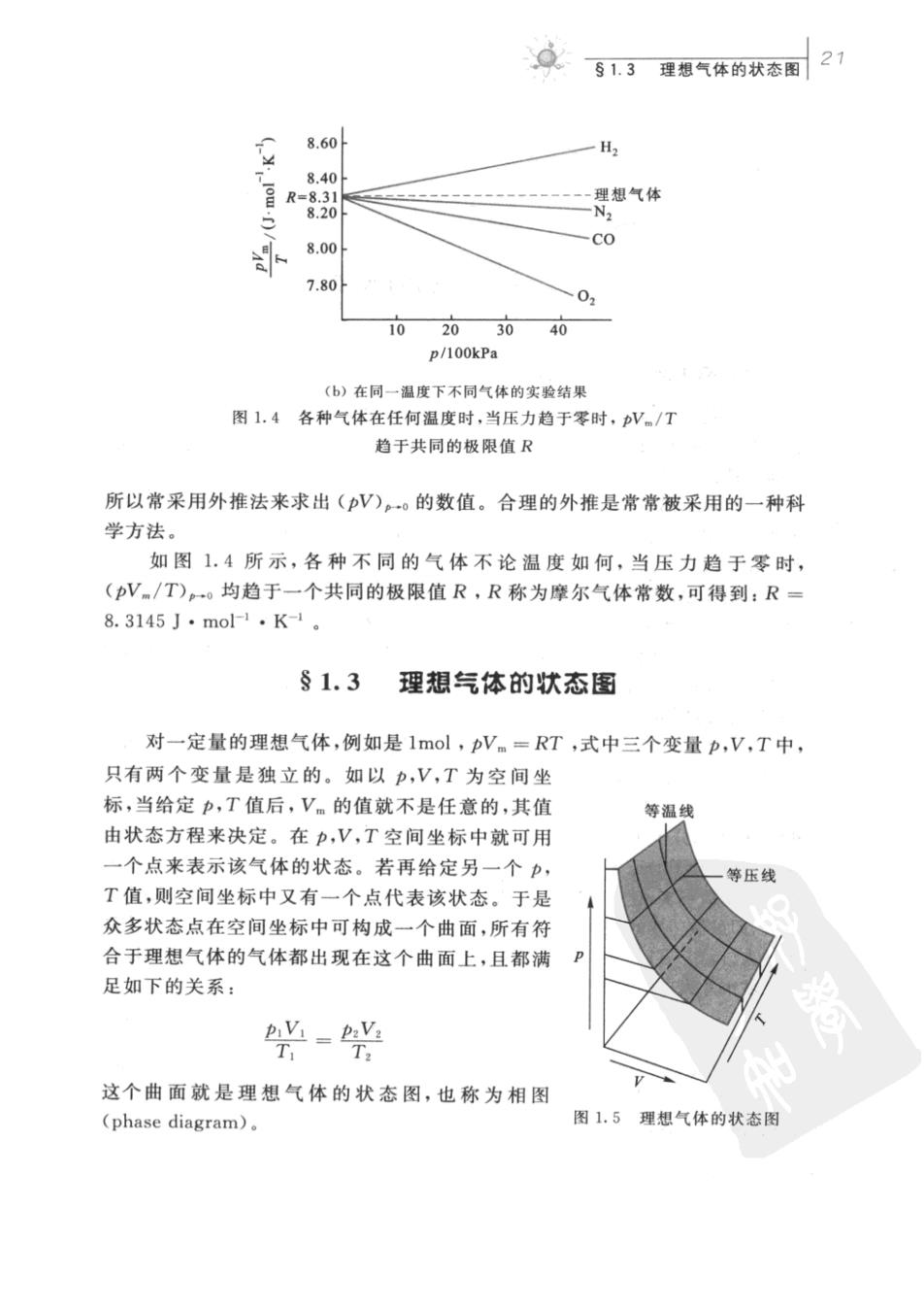
众913理想气体的状态围21 8.60 H 8.40 8.00 co 7.80 0 10 20 3040 p/100kPa (b)在同一温度下不同气体的实验结果 图1.4各种气体在任何温度时,当压力趋于零时,V。/T 趋于共同的极限值R 所以常采用外推法来求出(V),。的数值。合理的外推是常常被采用的一种科 学方法。 如图1.4所示,各种不同的气体不论温度如何,当压力趋于零时, (pV./T)-。均趋于一个共同的极限值R,R称为摩尔气体常数,可得到:R= 8.3145J·mo1·K-1。 §1.3理想气体的状态图 对一定量的理想气体,例如是1mol,Vm=RT,式中三个变量p,V,T中, 只有两个变量是独立的。如以p,V,T为空间坐 标,当给定p,T值后,V的值就不是任意的,其值 等温线 由状态方程来决定。在p,V,T空间坐标中就可用 一个点来表示该气体的状态。若再给定另一个, T值,则空间坐标中又有一个点代表该状态。于是 众多状态点在空间坐标中可构成一个曲面,所有符 合于理想气体的气体都出现在这个曲面上,且都满 足如下的关系: '=y T T. 这个曲面就是理想气体的状态图,也称为相图 (phase diagram)。 图1.5理想气体的状态图

22第=率气体缘 用等温面切割,就得到等温线(isotherm); 如用等压面切割,就得到等压线(isobar)。 读者试在: (1)p-V坐标图上画出理想气体在不同温度下的等温线, (2)在p一T坐标图上画出理想气体在不同压力下的等压线。 §1.4分子运动的速率分布 Maxwell速率分布定律 气体包含了为数很多的分子,它们在容器内作高速的无秩序运动,不难想 像,它们互碰的次数很多。如果某一个分子被连续碰撞,速率可能增加得很大, 但也可能因同时受几个分子自不同方向碰撞,而在瞬息间相对的“静止”。每 个分子的速率都随时间而不断地改变,并受概率的支配。但分子整体的总动能 或平均速率在定温下却保持不变。当气体分子处于稳定状态时,速率的分布遵 循一定的统计规律。 我们无法很精确地知道具有某一给定速率的分子究竟有多少,因为一般地 讲在某一瞬间速率正好是的分子可能很少,甚至可能没有这样的分子。但是 可以提出这样的问题,即速率落在一定间隔v~v十d口内的分子有多少,落在哪 一个间隔中的分子数最多?(由于分子的数目很多,即使d很小,但在。~v十 d口的间隔内仍包含着为数众多的分子)。这就是本节中所要讨论的问题。 Maxwell于l859年首先导出了分子速率的分布公式,后来Boltzmann用统 计力学的方法也得到相同的公式,从而加强了Maxwell公式的理论基础。 今设容器内有N个分子,速率在v~v+du范围内的分子有dN。个, dN,/N表示分子速率在此范围中的分子占总分子数的分数。对于一个分子来 说,就是该分子的速率在o~v十du间隔中的概率。dN,显然与N和du有关, 即总分子数越多,速率间隔越大,则dN。必越大。同时dN,也与速率。的大小 有关,即虽然速率的间隔相同,而速率不同,则其分子数也不同(这正如在一个城 市的人口,10~11岁和2021岁,两个年龄段都相差1岁,但这两个年龄段人 口在城市总人口中所占的分数可能是不同的)。即 dN.oc Ndu或dN。=Nf(o)du (1.20) f(o)是一个与v及温度有关的函数,称为分布函数(distribution func- tion),它的意义相当于du=1时,即速率在v至v+l之间的分子在总分子中所 占的分数。Maxwell证得