
个体与集成一简单分析 口考虑二分类问题,假设基分类器的错误率为: P(hi(x)卡f(c)=e 口假设集成通过简单投票法结合T个分类器,若有超过半数的基分类 器正确侧分类就正确 H(x)=sign
个体与集成 – 简单分析 p 考虑二分类问题,假设基分类器的错误率为: p 假设集成通过简单投票法结合�个分类器,若有超过半数的基分类 器正确则分类就正确

个体与集成一简单分析 口假设基分类器的错误率相互独立,则由Hoeffding不等式可得集成 的错误率为: T/2 P(H(c)≠f()》= (图)a-gert ≤m(7-2) ▣上式显示,在一定条件下,随着集成分类器数目的增加,集成 的错误率将指数级下降,最终趋向于0
个体与集成 – 简单分析 p 假设基分类器的错误率相互独立,则由Hoeffding不等式可得集成 的错误率为: p 上式显示,在一定条件下,随着集成分类器数目的增加,集成 的错误率将指数级下降,最终趋向于0

个体与集成一简单分析 ▣ 上面的分析有一个关键假设:基学习器的误差相互独立 口现实任务中,个体学习器是为解决同一个问题训练出来的,显然 不可能互相独立 ▣事实上,个体学习器的“准确性”和“多样性”本身就存在冲突 口如何产生“好而不同”的个体学习器是集成学习研究的核心 口集成学习大致可分为两大类
个体与集成 – 简单分析 p 上面的分析有一个关键假设:基学习器的误差相互独立 p 现实任务中,个体学习器是为解决同一个问题训练出来的,显然 不可能互相独立 p 事实上,个体学习器的“准确性”和“多样性”本身就存在冲突 p 如何产生“好而不同”的个体学习器是集成学习研究的核心 p 集成学习大致可分为两大类

集成学习 ▣ 个体与集成 ▣Boosting Adaboost GBDT ▣Bagging与随机森林 口结合策略 ●平均法 ●投票法 ●学习法 口多样性 ●误差分歧分解 多样性度量 ● 多样性扰动
集成学习 p 个体与集成 p Boosting l Adaboost l GBDT p Bagging与随机森林 p 结合策略 l 平均法 l 投票法 l 学习法 p 多样性 l 误差-分歧分解 l 多样性度量 l 多样性扰动
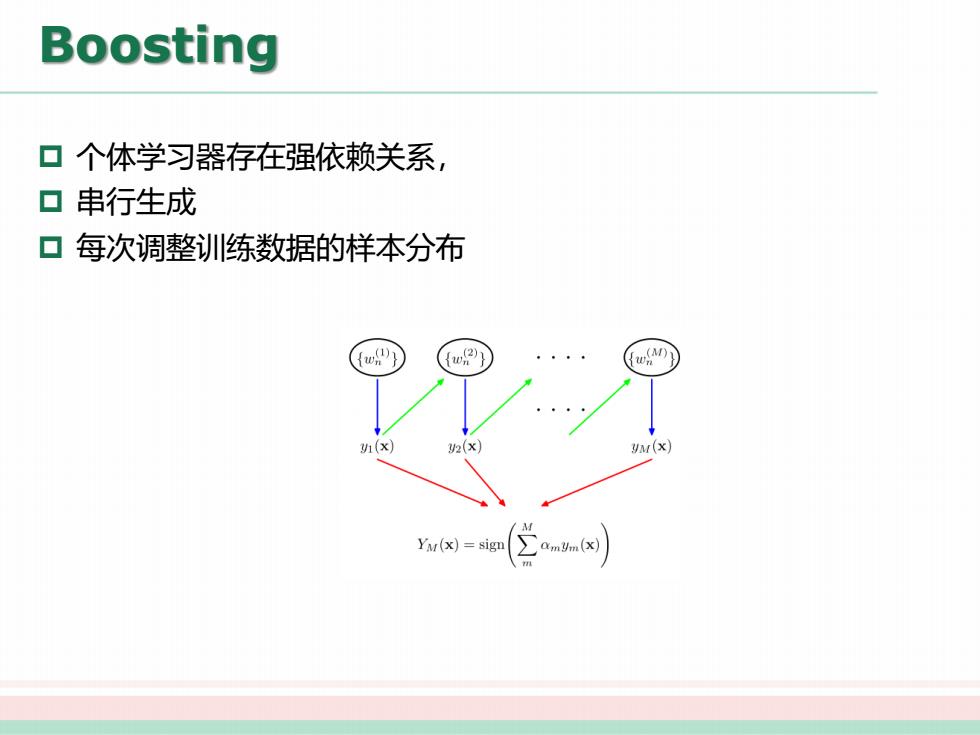
Boosting 口个体学习器存在强依赖关系, ▣串行生成 口每次调整训练数据的样本分布 (x) 2(x yM(x) /A Yu(x)=sign CamUm(x)
Boosting p 个体学习器存在强依赖关系, p 串行生成 p 每次调整训练数据的样本分布