
西北大学化工原理电子教案 1 众,作用于abc过面上的压强为P+×必x.因此作用于该两表面上的 20x 2 Ox 压力分别为: op Sx 2 图1-6流体微元的受力平衡 (2)体积力设作用于单位质量流体上的体积力在x方向的分量为X,则微元所受的体积力 在x方向的分量为Xp远(式中p为密度)。同理,在y及:轴上微元所受的体积力分别 为YpoxSv&Y和Zp&x8v&。 该流体处于静止状态,外力之和必等于零。对x方向,可写成: p--(p+5正+=0 各项均除以微元体的流体质量py正可得: X-1@p 0 p ox 同理 y-1p=0 (1-6) pay z、1 =0 poz 此式称为欧拉平衡方程。等式左方为单位质量流体所受的体积力和压力。 若将该微元流体移动d山距离,此距离对x,y,z轴的分量为dx,dy,d止,将上列方程 组分别乘以c,,止并相加可得: 6
西北大学化工原理电子教案 x x p p δ ∂ ∂ ×− 2 1 ,作用于 a’b’c’d’面上的压强为 x x p p δ ∂ ∂ ×+ 2 1 。因此作用于该两表面上的 压力分别为: zyx x p p ⎟ δδδ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ×− 2 1 和 zyx x p p ⎟ δδδ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ×+ 2 1 z y O d’ c’ b’ a’ d c b a A x x x p p δ ∂ ∂ ×− 2 1 x x p p δ ∂ ∂ ×+ 2 1 图 1-6 流体微元的受力平衡 (2) 体积力 设作用于单位质量流体上的体积力在 x 方向的分量为 X,则微元所受的体积力 在 x 方向的分量为 ρδ δ δzyxX (式中ρ为密度)。同理,在 y 及 z 轴上微元所受的体积力分别 为 ρδ δ δzyxY Y 和 ρδ δ δzyxZ 。 该流体处于静止状态,外力之和必等于零。对 x 方向,可写成: 0 2 1 2 1 ⎟ + = ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ⎟ ×+− ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ×− zyxXzyx x p pzyx x p p δδδ δδρδδδδ 各项均除以微元体的流体质量 ρδ δ δzyx 可得: ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎬ ⎫ = ∂ ∂ − = ∂ ∂ − = ∂ ∂ − 0 1 0 1 0 1 z p Z y p Y x p X ρ ρ ρ 同理 (1-6) 此式称为欧拉平衡方程。等式左方为单位质量流体所受的体积力和压力。 若将该微元流体移动 dl 距离,此距离对 x,y,z 轴的分量为 dx,dy,dz,将上列方程 组分别乘以 dx,dy,dz 并相加可得: 6

西北大学化工原理电子教案 吧d+2d+d止 -(Xdx +Ydy+Zd2)=0 (1-7) 表示两种力对微元流体作功之和为零。由于静止流体压强仅与空间位置有关,而与时间 无关,所以,式(1-7)左侧第一项括号内即为压强的全微分dp,于是: d迎=Xdk+Yy+Zt (1-8) 式(1-8)是流体平衡的一般表达式。等式两边分别表示压力和体积力所作的功。 平衡方程在重力场中的应用如流体所受的体积力仅为重力,并取?轴方向与重力方向相 反,则:X=0,Y=0,Z=g。将此代入式(1-8),得: dp+pgdz=0 +在=0 (1-9) 设流体不可压缩,即密度ρ与压强无关,可将上式积分得: 卫+g=常数 (1-10) 对于静止流体中任意两点1和2,如图1-7所示: 1 图1-7重力场中静压强分布 +g=+g (1-11) 0 0 或 P2=P+P8(a1-2)=P1+P8h (1-12) 注意:式(1-10)、(1-11)、(1-12)三式仅适用于在重力场中静止的不可压缩流体
西北大学化工原理电子教案 ( 0 1 =++−⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ ZdzYdyXdxdz z p dy y p dx x p ρ ) (1-7) 表示两种力对微元流体作功之和为零。由于静止流体压强仅与空间位置有关,而与时间 无关,所以,式(1-7)左侧第一项括号内即为压强的全微分 dp,于是: ZdzYdyXdx dp ++= ρ (1-8) 式(1-8)是流体平衡的一般表达式。等式两边分别表示压力和体积力所作的功。 平衡方程在重力场中的应用 如流体所受的体积力仅为重力,并取 z 轴方向与重力方向相 反,则:X=0,Y=0,Z=-g。将此代入式(1-8),得: + ρgdzdp = 0 ∫ ∫ dzg =+ 0 dp ρ (1-9) 设流体不可压缩,即密度ρ与压强无关,可将上式积分得: gz =+ 常数 p ρ (1-10) 对于静止流体中任意两点 1 和 2,如图 1-7 所示: h z1 z2 图 1-7 重力场中静压强分布 2 2 1 1 gz p gz p +=+ ρρ (1-11) = + ρ − = + ρghpzzgpp 12 121 或 )( (1-12) 注意:式(1-10)、(1-11)、(1-12)三式仅适用于在重力场中静止的不可压缩流体。 7

西北大学化工原理电子教案 1.2.2压强能与位能 g项实质上是单位质量流体所具有的位能。P相应地是单位质量流体所具有的压强能。 静止流体存在着两种形式的势能(位能和压强能),在同一种静止流体中处于不同位置的微 元其位能和压强能各不相同,但其和即总势能保持不变。若以符号一 表示单位质量流体 的总势能,则 =g+ (1-13) 式中乎具有与压强相同的因次,可理解为一种虚拟的压强。 乎=Pg+p (1-14) 对不可压缩流体,同种静止流体各点的虚拟压强处处相等。注意:乎的大小与密度有 关,即与流体种类有关。 1.2.3压强的表示方法 压强的其它表示方法压强的大小除直接以P表示外,工程上常间接地以流体柱高度表示, 如用米水柱或毫米汞柱等。液柱高度h与压强的关系为: p=pgh (1-15) 注意:当以液柱高度h表示压强时,必须同时指明为何种流体。 1atm(标准大气压)=1.013×103Pa,相当于760mmHg或10.33mH20。 压强的基准压强的大小常以两种不同的基准来表示:一是绝对真空:二是大气压强。以绝 对真空为基准量得的压强称为绝对压强,以大气压强为基准量得的压强称为表压或真空度。 表压 大气压 绝对压力 真空度 P2 绝对压力 绝对真空 图1-8压强的基准和量度 表压=绝对压一大气压:真空度=大气压一绝对压。 8
西北大学化工原理电子教案 1.2.2 压强能与位能 gz 项实质上是单位质量流体所具有的位能。 ρ p 相应地是单位质量流体所具有的压强能。 静止流体存在着两种形式的势能(位能和压强能),在同一种静止流体中处于不同位置的微 元其位能和压强能各不相同,但其和即总势能保持不变。若以符号 表示单位质量流体 的总势能,则 P ρ (1-13) 式中 P 具有与压强相同的因次,可理解为一种虚拟的压强。 (1-14) 对不可压缩流体,同种静止流体各点 P ρρ p gz += P = ρgz + p 的虚拟压强处处相等。注意:P 的大小与ρ密度有 关,即与流体种类有关。 1.2.3 压强的表示方法 压强的大小除直接以 Pa 表示外,工程上常间接地以流体柱高度表示, (1-15) 注意:当以液柱高度 h 表示压强时, O。 强的基准 压强的大小常以两种不同的基准来表示:一是绝对真空;二是大气压强。以绝 图 1-8 压强的基准和量度 表压 = 绝对压-大气压;真 压强的其它表示方法 如用米水柱或毫米汞柱等。液柱高度 h 与压强的关系为: p = ρgh 必须同时指明为何种流体。 1atm(标准大气压)=1.013×105 Pa,相当于 760mmHg或 10.33mH2 压 对真空为基准量得的压强称为绝对压强,以大气压强为基准量得的压强称为表压或真空度。 空度 = 大气压-绝对压。 绝对真空 p1 大气压 绝对压力 绝对压力 表压 真空度 p2 8

西北大学化工原理电子教案 1.2.4压强的静力学测量方法 压强的测量仪表很多,本节仅介绍应用静力学原理测量压强的方法。 简单测压管。最简单的测压管如图1-9所示。 Pa=pa+Rpg A点的表压为: PA-Pa=Rpg (1-16) 图1-9简单测压管 简单测压管只适用于高于大气压的液体压强的测定,不能适用于气体。此外,如被测压强 P4过大,读数R也将过大,测压很不方便。反之,如被测压强与大气压过于接近,读数R将 很小,使测量误差增大。 U形测压管图1-10表示用U形测压管测量容器中的A点压强。在U形玻璃管内放有某种 液体作为指示液。指示液必须与被测流体不发生化学反应且不互溶,其密度大于被测流体 的密度p 由静力学原理可知,在同一种静止流体内部等高面即是等压面, 即p1=P2 PI=Pa+pghi p2=Pa+pigR 由此可求得A点的压强为 PA Pa+PgR-pghi 图1-10U型测压管 A点的表压为 Pa -Pa PigR -pgh (1-17) 若容器内为气体,则由气柱h造成的静压强可以忽略,得 PA -Pa =PgR (1-18) 此时U形测压管的指示液读数R表示A点压强与大气压之差,读数R即为A点的表压。 U形压差计如U形测压管的两端分别与两个测压口相连,则可以测得两测压点之间的压 差,故称为压差计。图1-11表示U形压差计测量均匀管内作定态流动时A、B两点的压差。 因U形管内的指示液处于静止,故位于同一水平面1、2两点的压强 pI=pa+pgh 与 P2=PB+pg(h2-R)+pgR
西北大学化工原理电子教案 1.2.4 节仅介绍应用静力学原理测量压强的方法。 简单 A 点的表压为: pA − pa = Rρg (1-16) 图 1-9 简单测压管 简单测压管只适用于高于大气压的液体压强的测定,不能适 压强的静力学测量方法 压强的测量仪表很多,本 测压管 最简单的测压管如图 1-9 所示。 pA = pa + Rρg 用于气体。此外,如被测压强 形测压管 图 1-10 表示用U形测压管测量容器中的 A 点压强。在U形玻璃管内放有某种 学原理可知, 在同一种静止流体内部等高面即是等压面, 即p1 p1 = pA + ρgh1 由此可求得 A 点的 ρigR − ρgh1 图 1-10 U型测压管 A点的表压为 (1-18) 此时 U 形测压管的指示液读数 R 表示 形压差计 如 U 形测压管的两端分别与两个测压口相连,则可以测得两测压点之间的压 与 p2 = p pA过大,读数R也将过大,测压很不方便。反之,如被测压强与大气压过于接近,读数R将 很小,使测量误差增大。 U 液体作为指示液。指示液必须与被测流体不发生化学反应且不互溶,其密度ρi大于被测流体 的密度ρ。 由静力 = p2 p2 = pa + ρigR 压强为 pA = pa + pA − pa = ρigR − ρgh1 (1-17) 若容器内为气体,则由气柱h1造成的静压强可以忽略,得 pA − pa = ρigR A 点压强与大气压之差,读数 R 即为 A 点的表压。 U 差,故称为压差计。图 1-11 表示 U 形压差计测量均匀管内作定态流动时 A、B 两点的压差。 因 U 形管内的指示液处于静止,故位于同一水平面 1、2 两点的压强 p1 = pA + ρgh1 BB + ρg(h2 − R) + ρigR 9
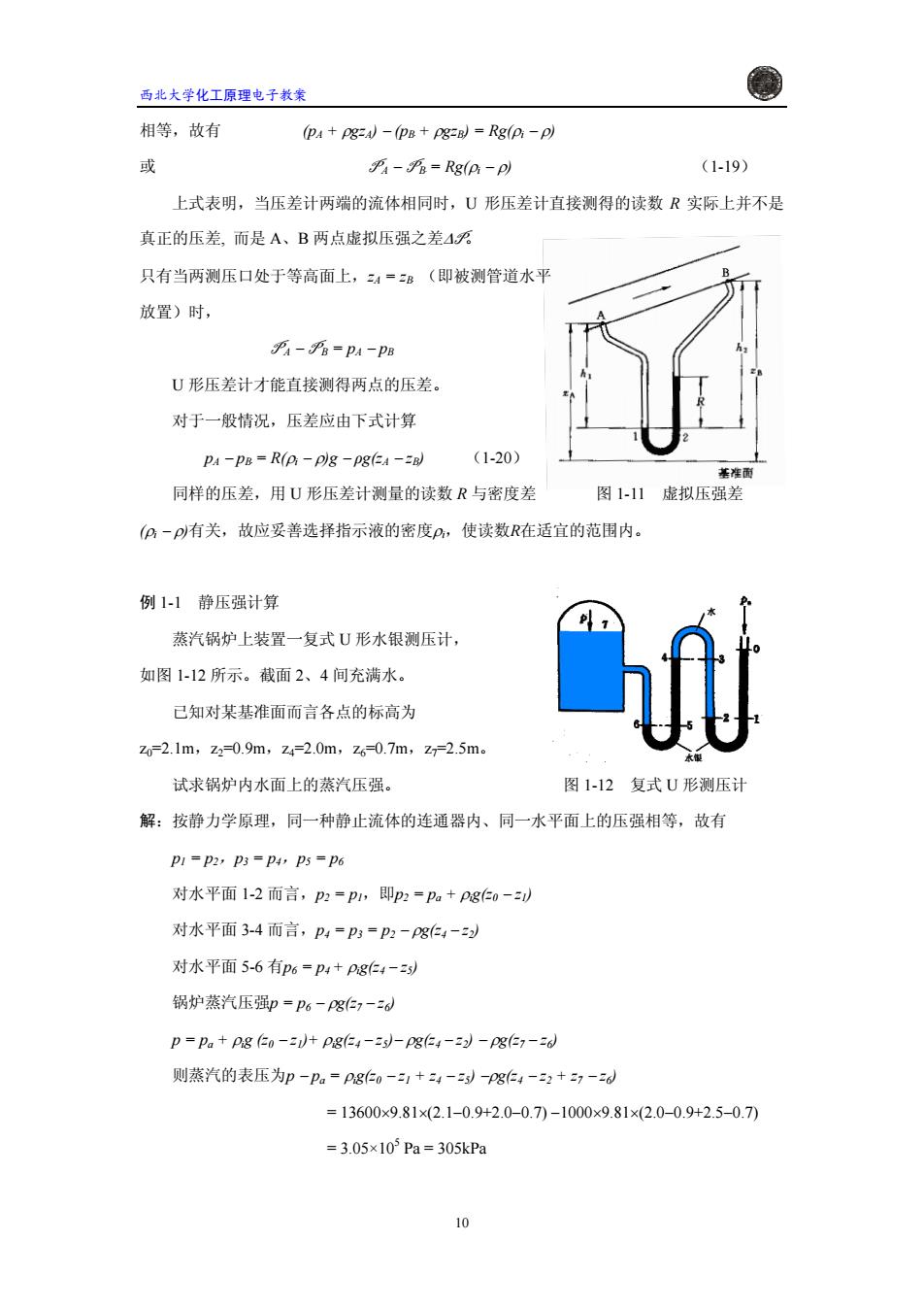
西北大学化工原理电子教案 相等,故有 (PA+P8=A)-(PB+Pg=B)=Rg(p:-p) 或 =Rg(pi-p) (1-19) 上式表明,当压差计两端的流体相同时,U形压差计直接测得的读数R实际上并不是 真正的压差,而是A、B两点虚拟压强之差4万 只有当两测压口处于等高面上,4=B(即被测管道水平 放置)时, 乎A-%=pA-PB U形压差计才能直接测得两点的压差。 对于一般情况,压差应由下式计算 PA-PB=R(Pi-p)g -p8(A-B) (1-20) 基准面 同样的压差,用U形压差计测量的读数R与密度差 图111虚拟压强差 (P一p有关,故应妥善选择指示液的密度P,使读数R在适宜的范围内。 例1-1静压强计算 蒸汽锅炉上装置一复式U形水银测压计, 如图1-12所示。截面2、4间充满水。 己知对某基准面而言各点的标高为 Z0-2.1m,z2=0.9m,Z4=2.0m,z6=0.7m,z斤2.5m。 试求锅炉内水面上的蒸汽压强。 图1-12复式U形测压计 解:按静力学原理,同一种静止流体的连通器内、同一水平面上的压强相等,故有 P1=P2,P3=P4,P5=P6 对水平面1-2而言,p2=p,即p2=Pa+P8仁0-) 对水平面3-4而言,P4=P3=p2-Pg4-) 对水平面5-6有p6=p4+P8e4-到 锅炉蒸汽压强p=P6-Pg仁1-6d p=Pa+pg (o-1)+P8(4-Es)-p8(E4-22)-pg(=7-36) 则蒸汽的表压为p-pa=P80-1+24-)-Pg4-2+27-d =13600×9.81×(2.1-0.9+2.0-0.7)-1000×9.81×(2.0-0.9+2.5-0.7) =3.05×105Pa=305kPa 10
西北大学化工原理电子教案 相等,故有 (pA + ρgzA) − (pB + B ρgzBB) = Rg(ρ − ρ) i 或 P A − P B = Rg( B ρ (1-19) 是 真正 − ρ) i 上式表明,当压差计两端的流体相同时,U 形压差计直接测得的读数 R 实际上并不 的压差, 而是 A、B 两点虚拟压强之差ΔP。 只有当两测压口处于等高面上,zA = zBB (即被测管道水平 P A − P B = pA − pB U 形压差计才能直接测得两点的压差。 放置)时, 对于一般情况,压差应由下式计算 pA − pB = R( B ρi − ρ)g − ρg(zA − zBB (1-20) 同样 R 图 1-11 虚拟压强差 (ρi − 1-1 静压强计算 一复式 U 形水银测压计, 如图 z0=2 z7=2.5m。 图 1-12 复式 U 形测压计 解: p1,即p2 = pa + ρig(z0 − z1) ρg(z4 − z2) − ρg(z7 − z6) z7 − z6) ×(2.0−0.9+2.5−0.7) ) 的压差,用 U 形压差计测量的读数 与密度差 ρ)有关,故应妥善选择指示液的密度ρi,使读数R在适宜的范围内。 例 蒸汽锅炉上装置 1-12 所示。截面 2、4 间充满水。 已知对某基准面而言各点的标高为 .1m,z2=0.9m,z4=2.0m,z6=0.7m, 试求锅炉内水面上的蒸汽压强。 按静力学原理,同一种静止流体的连通器内、同一水平面上的压强相等,故有 p1 = p2,p3 = p4,p5 = p6 对水平面 1-2 而言,p2 = 对水平面 3-4 而言,p4 = p3 = p2 − ρg(z4 − z2) 对水平面 5-6 有p6 = p4 + ρig(z4 − z5) 锅炉蒸汽压强p = p6 − ρg(z7 − z6) p = pa + ρig (z0 − z1)+ ρig(z4 − z5)− 则蒸汽的表压为p − pa = ρig(z0 − z1 + z4 − z5) −ρg(z4 − z2 + = 13600×9.81×(2.1−0.9+2.0−0.7) −1000×9.81 = 3.05×105 Pa = 305kPa 10