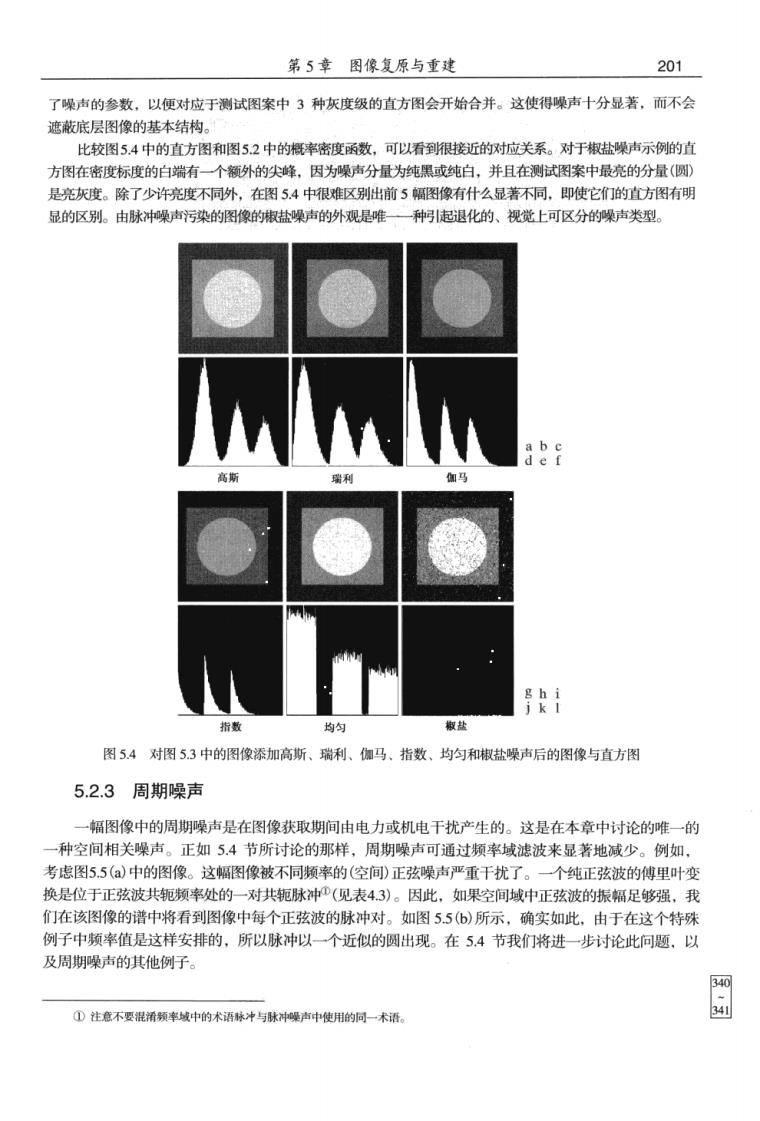
第5章图像复原与重建 201 了噪声的参数,以便对应于测试图案中3种灰度级的直方图会开始合并。这使得噪声十分显著,而不会 遮蔽底层图像的基本结构。 出校图5.4中的有方图和图52中的概率密度函数,可以看到很接近的对应关系。对于椒盐噪声示例的直 方图在密度标度的白端有一个额外的尖峰,因为噪声分量为纯黑或纯白,并且在测试图案中最亮的分量(圆) 是亮灰度。除了少许亮度不同外,在图5.4中很难区别出前5幅图像有什么显著不同,即使它们的直方图有明 显的区别。由脉冲噪声污染的图像的椒盐噪声的外观是唯一一种啊引起退化的、视觉上可区分的噪声类型。 指数 均匀 散盐 图54对图5.3中的图像添加高斯、瑞利、伽马、指数、均匀和椒盐噪声后的图像与直方图 5.2.3周期噪声 一幅图像中的周期噪声是在图像获取期间由电力或机电干扰产生的。这是在本章中讨论的唯一的 一种空间相关噪声。正如5.4节所讨论的那样,周期噪声可通过频率域滤波来显著地减少。例如 考虑图5.5(a)中的图像。这幅图像被不同频率的(空间)正弦噪声严重干扰了。一个纯正弦波的傅里叶变 换是位于正弦被共距顿率处的一对共轭脉神①(见表43)。因此,如果空间域中正弦波的振辐足够强我 们在该图像的谱中将看到图像中每个正弦波的脉冲对。如图55⑥)所示,确实如此,由于在这个特殊 例子中频率值是这样安排的,所以脉冲以一个近似的圆出现。在5.4节我们将进一步讨论此问题,以 及周期噪声的其他例子。 ①注意不要混淆颗率域中的术语脉冲与琳冲燥声中使用的同一未语

202 数字图像处理(第三版) a b 图55(a)被正弦噪声污染的图像:(6)谱(每对共轭脉冲对应于一个正弦波(原图像由NASA提) 5.2.4噪声参数的估计 典型地。周期噪声的参数是通过检测图像的傅里叶谱来估计的。正如前几节提及的那样,周期噪 声趋向于产生频率尖峰,甚至通过视觉分析也经常可以检测到这些尖峰。另一种方法是试图直接由图 像推断出噪声分量的周期性,但这仅在非常简单的情况下才是可能的。在噪声尖峰格外显著或可以使 用关于干扰的频率分量一般位置的某些知识时,自动分析是可能的 噪声PDF的参数一般可以从传感器的技术说明中得知,但对于特殊的成像装置通常需要估计这 些参数。如果成像系统可用,那么研究系统噪声特性的一种简单方法是获取一组“平坦”环境的图像 例如,在光学传感器的情况下,这像对一个光照均匀的纯色灰度板成像一样简单。结果图像是典型的 系统噪声的良好指示器。 当仅有通过传感器生成的图像可用时,通常可由合理的恒定灰度值的一小部分来估计PDF的 参数。例如,图5.6所示的垂直条带(150×20像素)是从图5.4中所示的高斯、瑞利和均匀图像中截取 的。所显示的直方图是使用这些小条带的图像数据计算出来的。与图5.6中的直方图对应的图5.4中 的直方图.是图5.4(d)、图54(e)和图5.4k)这三组直方图中间的一组。我们可以看出,这些对应的 直方图的形状非常接近于图5.6中的直方图的形状。由于缩放的原因,它们的高度不同,但形状明 显类似。 a b c 图5.6使用小条带(显示为桶图从图5.4中的(a)高斯、()瑞利和(©)均噪声图像计算的直方图 来自图像条带数据的最简单的用途是计算灰度级的均值和方差。考虑由S表示的一个条带(子图 像),并今P5(),i=0,1,2,…,L-1表示S中像素灰度的概率估计(归一化直方图饱,其中L是整 个图像中可能的灰度数(例如,对于8比特图像,L为256)。如第3章那样,我们估计S的均值和方 差如下: -P() (5.2-15) 图 。-公-ana (5.2-16)

第5章图像复原与重建 203 直方图的形状确定最接近的PDF匹配。如果其形状近似于高斯,那么均值和方差正是我们所需 要的.因为高斯PDF完全由这两个参数指定。对于5.22节讨论的其他形状,我们使用均值和方差米 解出参数α和b。使用不同的方法来处理脉冲噪声,因为需要的估计是黑、白像素发生的实际概率。 获得这些估计值需要黑白像素是可见的,因此为了计算直方图,图像中需要有一个相对恒定的中等灰 度区域。对应于黑、白像素的尖峰的高度是式(5.214)中P.和P,的估计值 5.3只存在噪声的复原—空间滤波 当一幅图像中唯一存在的退化是噪声时,式(5.1-1)和式(5.1-2)变成 g(x.y)=f(x.y)+n(x.y) (5.3-) G(,v)=F(M,)+N(u,v) (5.3-2) 噪声项是未知的,故从gK)或G私,中减去它们不是一个现实的选择。在周期噪声的情祝下,由G山,) 的谱来估计M4,通常是可能的、正如5.2.3节所述。在这种情况下,从G(4,)中减去N山,)可得到 原图像的一个估计。然而,这种类型的知识通常只是例外而不是规律。 当仅存在加性噪声的情况下可以选择空间滤波方法。空间滤波已在第3章中详细讨论过了。 除了执行一种特定的滤波来计算特性以外,下面实现的所有滤波的机理完全与35节和3.6节中讨论 过的一样。 5.3.1均值滤波器 在本节中,我们简要地讨论35节中介绍过的空间滤波器的降噪能力,并探讨一些其他的滤波器, 这些滤波器的性能在许多情况下要优于3.5节中所讨论的滤波器的性能。 算术均值滤波器 这是最简单的均值滤波器。令S,表示中心在点(x,y)处、大小为mxn的矩形子图像窗口(邻域) 的一组坐标。算术均值滤波器在S。定义的区域中计算被污染图像 假设m和是奇整数 gx,)的平均值。在点(xy)处复原图像子的值.就是简单地使用5 定义的区域中的像素计算出的算术均值,即 fx.)产mm点 1∑g,0 (5.33) 这个操作可以使用大小为m×n的一个空间滤波器来实现。其所有的系数均为其值的1mn。均值滤波 平滑一幅图像中的局部变化。虽然模糊了结果,但降低了噪声。 几何均值滤波器 使用几何均值滤波器复原的一幅图像由如下表达式给出: ixy=[Π8,0 (5.34) 其中,每个复原的像素由子图像窗口中像素的乘积的1m次幂给出。如例5.2所示,几何均值滤波 器实现的平滑可与算术均值滤波器相比。但这种处理中丢失的图像细节更少

204 数字图像处理(第三版) 谐波均值滤波器 谐波均值滤波操作由如下表达式给出: f(x.y)=- (5.3.5 1 点n 谐波均值滤波器对于盐粒噪声效果较好,但不适用于胡椒噪声。它善于处理像高斯噪声那样的其他 噪声 逆谐波均值滤波器 逆谐波均值滤波器基于如下表达式产生一幅复原的图像: ∑ga,)e x)= (5.3-6) 其中Q称为滤波器的阶数。这种滤波器适合减少或在实际中消除椒盐噪声的影响。当Q值为正时, 该滤波器消除胡椒噪声:当Q值为负时,该滤波器消除盐粒噪声。但它不能同时消除这两种噪声。注 意。当Q=0时,逆谐波均值滤波器简化为算术均值滤波器:而当Q=-1时,则为谐波均值滤波器 例52均值滤波器的说明 图5.7(a)显示了一块电路板的8比特X射线图像,图5.7(6)显示了相同的图像,但图像已被均值为零 方差为400的加性高斯噪声污染了。对于这种类型的图像,这是非常严重的噪声。图5.7()和图5.7(@)分 别显示了使用大小为3×3的算术均值滤波器和同样大小的几何均值滤波器滤除噪声后的结果。尽管这两 种噪声滤波器对噪声的衰减都起到了作用,但几何均值滤波器并未像算术均值滤波器那样使图像变得模 糊。例如,图像顶部的连接片在图5.7()中比在图5.7(c)中更为清晰。图像的其他部分同样如此。 abcd出 图5.7(a)X射线图像:(6)被加性高斯噪声污染的图像:(@)使用大小为3x3的 算术均值滤波器对图 像滤波后的结果(@使用相同大小的几何均值滤波 器对图像滤波后的结果(原图像由Lixi公司的Joseph E Pascemte先生提供 图5.8(a)显示了同样的电路图像,但被概率为0.1的胡椒噪声污染了。类似地,图5.8(b)显示了已被 具有相同概率的盐粒噪声污染了的图像。图5.8(C)显示了使用Q=1.5的逆谐波均值滤波器对图5.8(a)滤 波的结果。图5.8(@显示了使用Q=-15的逆谐波均值滤波器对图5.86)滤波后的结果。两种滤波器都有 很好的去除噪声的效果。这种正阶滤波器除了使得暗区稍微有些淡化和模糊之外,都使背景变得更为清 圆版的收

第5章图像复原与重建 205 eH出HH 图5.8(a)被概率为0.1的胡椒噪声污染的图像:()被相同概率的盐粒噪声污染的 图像:()使用大小为3x3,阶数为15的逆 波均值滤波器对图(a)滤 后的结果:(@)使用Q=-1.5的逆谐波均值滤波器对图(6)滤波后的结果 总之,算术均值滤波器和几何均值滤波器(尤其是后者)更适合于处理高斯或均匀随机噪声。逆谐波 均值滤波器更适合于处理脉冲噪声,但它还有一个缺点,即必须知道噪声是暗噪声还是亮噪声,以便于 为Q选择的正确的符号。如果Q的符号选择错了,则可能会引起灾难性的后果,如图59所示。下面几 节讨论的一些滤波器可消除这种缺点。 图59在逆谐波滤波中选择错误符号的结果:()使用大小为3x3且Q=-15的逆谐 波滤波器对图5.8(a)滤波后的结果;(6)当Q=1.5时对图5.8(6)滤波后的结果 5.3.2统计排序滤波器 3.5.2节介绍过统计排序滤波器。我们现在扩充那一节的讨论,并介绍其他一些统计排序滤波器 正如3.5.2节所述,统计排序滤波器是空间域滤波器,空间滤波器的响应基于由该滤波器包围的图像 区域中的像素值的顺序(排序)。排序结果决定滤波器的响应 中值滤波器 最著名的统计排序滤波器是中值滤波器,如其名称所暗示的那样,它使用一个像素邻域中的灰 度级的中值来替代该像素的值,即 y)=mediang(s.) (5.37) 在化,y)处的像素值是计算的中值。中值滤波器的应用非常普遍,因为对于某些类型的随机噪声,它 们可提供良好的去噪能力,且比相同尺寸的线性平滑滤波器引起的模糊更少。在存在单极或双极脉 冲噪声的情况下,中值滤波器尤其有效。事实上,正如下面的例5.3所示,中值滤波器对于这种噪 声污染的图像可得到非常好的处理效果。这种滤波器中值的计算和实现已在352节中进行了详细网 的讨论