
随机误差符合正态分布 1.大误差出现的几率小,小误差出现的几率大。 2,绝对值相等的正负误差出现的几率相等。 3,误差为零的测量值出现的几率最大。 所有测量值出现的概率总和应为1,即 (x-4)2 2 e dx =1 -00 求变量在某区间出现的概率,即对该区间求积分 (x-)2 P(a,b)=- 20 dx N2π
随机误差符合正态分布 1.大误差出现的几率小,小误差出现的几率大。 2.绝对值相等的正负误差出现的几率相等。 3.误差为零的测量值出现的几率最大。 所有测量值出现的概率总和应为 1,即 e d 1 2 π 1 ( , ) 2 2 2 ( ) −∞ ∞ = = − ∞ − ∫− ∞ P x x σ µ σ 求变量在某区间出现的概率,即对该区间求积分 P a b x x b a e d 2 π 1 ( , ) 2 2 2 ( ) σ µ σ − − ∫ =
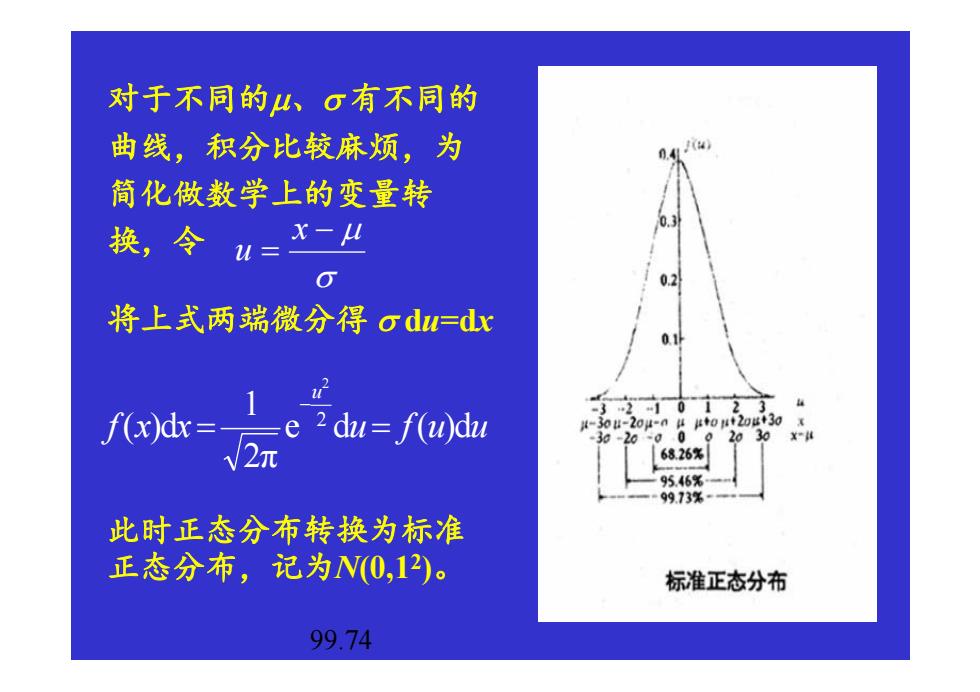
对于不同的山、o有不同的 曲线,积分比较麻烦,为 简化做数学上的变量转 换,令1= X-4 0 将上式两端微分得odu=dx 12 f(x)dx=-e 2du=f(u)du 30-204-n 2π 6826% 95.46% 99.73%- 此时正态分布转换为标准 正态分布,记为N(0,1)。 标准正态分布 99.74
对于不同的µ、σ 有不同的 曲线,积分比较麻烦,为 简化做数学上的变量转 换,令 σ − µ = x u 将上式两端微分得 σ du=dx f x x u f u u u e d ( )d 2π1 ( )d 2 2 = = − 此时正态分布转换为标准 正态分布,记为N(0,12)。 99.74

u 积分P= e2du已被做成概率积分表 √2π0 正态分布概率积分表 面积 wl 面积 | 面积 0.0 0.0000 1.0 0.3413 20 0.4773 0.1 0.0398 1.1 0.3643 21 0.4821 02 0.0793 12 03849 22 0.4861 0.3 0.1179 1.3 04032 2.3 0.4893 4 0.1554 14 Q.192 2.4 0.4918 0.5 01915 1.5 04332 25 0.4938 0.6 0.2258 1.6 Q.4452 26 0.4953 0.7 0.2580 1.7 0.4554 27 0.4965 0.8 02881 1.8 0641 28 0.4974 0.9 0.3159 1.9 0.4713 29 0.4987
积分 已被做成概率积分表 P u u u e d 2 π 1 2 0 2 − ∫ =

u x-u P% M=士1 土0 G u+o P=2×0.3413=0.6826=68.26% u户±2 ±2o u-20 +2G P=2×04773=0.9546=95.46% M=±3 ±3a L-3G +3o P=2×0.4987=0.9974=99.74% <例>按照正态分布x在区间(-0.5o,+1.5o出现的概率 解:根据 =-4 0 可将h0.5o≤≤H1.5o变换为-0.5≤u≤1.5 查表u=0.5时面积为0.1915 u=1.5时面积为0.4332 则-0.5≤u≤1.5的总面积即为x在区间(4-0.5o, 4+1.5o)出现的概率P=0.1915+0.4332=0.6247
u x -μ x P % u=±1 ±σ µ-σ µ+σ P=2× 0.3413 = 0.6826 =68.26% u=± 2 ± 2σ µ-2σ µ+2σ P=2× 0.4773 = 0.9546 =95.46% u=± 3 ± 3σ µ-3σ µ+3σ P=2× 0.4987 = 0.9974=99.74% <例> 按照正态分布x在区间(µ-0.5σ, µ+1.5σ)出现的概率 解: 根据 σ x u − µ = 可将 µ-0.5σ ≤x ≤µ+1.5σ 变换为 -0.5≤u ≤1.5 查表 u=0.5 时 面积为0.1915 u=1.5 时 面积为0.4332 则-0.5≤ u ≤1.5的总面积即为x在区间( µ - 0.5σ , µ +1.5σ )出现的概率 P = 0.1915 + 0.4332=0.6247