工程流体力学 Engineering Fluld Mechanics 6-4 圆管中流体的层流流动 达西公式 128uLqv △p= πd4 由前述沿程损失公式: hr=△p/pg ad2 9=A。= 4 a hi P 128Mg=64uL☒ 64L2 =λ pg pgndA pv d d2g Re d 2g 12g 得: =64/Re 可见,层流流动的 沿程损失与平均流 速的一次方成正比 7
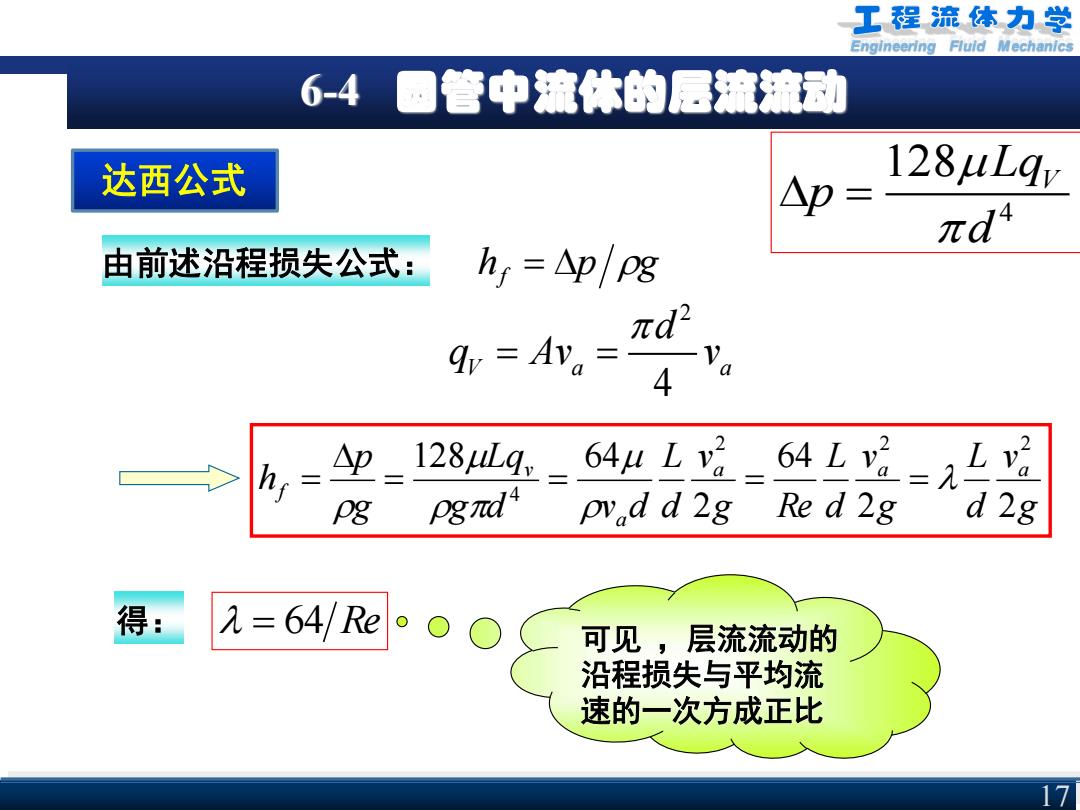
Engineering Fluid Mechanics 6-4 圆管中流体的层流流动 达西公式 h p g 由前述沿程损失公式: f = g v d L g v d L g Re v d L g d v d Lq g p h a a a a v f 2 2 64 2 128 64 2 2 2 4 = = = = = 2 4 V a a d q Av v = = 得: = 64 Re 可见 ,层流流动的 沿程损失与平均流 速的一次方成正比 17 4 128 LqV p d =

工程流体力学 Engineering Fluld Mechanics 6-4 圆管中流体的层流流动 其它系数 因沿程损失而消耗的功率:P=△pqv= 128Lq配 πd4 动痿正系数工“-灯说d1-以--2 優正系数工月=位rd4=∫(G-广 3 对动水平放蛋的恩置不,=。一号 8 此式对于圆管中粘 性流体的层流和紊 流流动都适用 8
Engineering Fluid Mechanics 6-4 圆管中流体的层流流动 其它系数 因沿程损失而消耗的功率: 4 2 128 d Lq P pq V V = = 动能修正系数: 0 r 3 2 2 3 8 0 0 A 0 1 16 ( ) d ( ) d 2 l a v A r r r r A v r = = − = 动量修正系数: 2 2 2 2 6 0 0 1 8 4 ( ) d ( ) d 3 x a v A r r r r A v r = = − = 对水平放置的圆管 0 2 2 8 0 v L r p w r r = = = = 此式对于圆管中粘 性流体的层流和紊 流流动都适用 18

工程流体力学 Engineering Fluld Mechanics 例题6-2 水平放置的毛细管黏度计,内径d0.50mm,两测点间的管长L=1.0m, 液体的密度p999kgm3,当液体的流量9r=880mm3/s时,两测点间的压 降Ap=1.0MPa,试求该液体的黏度。 解:假定流动为充分发展的层流,则 πdp- π(0.5×10-3)4×1.0×10 -=1.743×10-3(Pa2s) 128Lqv 128×1.0×880×10-9 4(880×10-9)×999 由于Re= Aqvp =1284<2000 πdu 元(0.5×10-3)×(1.743×10-3) 说明,层流的假定是对的,计算成立。 9
Engineering Fluid Mechanics 例 题 6-2 水平放置的毛细管黏度计,内径d=0.50mm,两测点间的管长L=1.0m, 液体的密度=999kg/m3 ,当液体的流量 =880mm3 /s时,两测点间的压 降 p=1.0MPa,试求该液体的黏度。 解: 19 V q 假定流动为充分发展的层流,则 4 3 4 6 9 πd π 3 (0.5 10 ) 1.0 10 1.743 128 128 1.0 880 10 10 ? V P Lq a s p − − − = = = ( ) 由于 9 3 3 4 4(880 10 ) 999 1284 2000 πd π(0.5 10 ) (1.743 10 ) V q Re − − − = = = 说明,层流的假定是对的,计算成立

工程流体力学 Engineering Fluld Mechanics 例题6-3 下图所示为内径20mm的倾斜放置的圆管,其中流过密度p-815.7kg/m3、黏 度0.04Pas的流体,已知截面1处的压强p1=9.806×10Pa,截面2处的压强 P2=19.612×10Pa。试确定流体在管中的流动方向,并计算流量和雷诺数。 解:为了确定流动方向,需要计算截面1和 2处流体总机械能的大小。由于等截面 6m 的管道在1和2处的流速相等,即它们 的动能相等,因而流动的方向决定于 该两处压强势能与位势能之和的大小。 在截面1处(p+pgh)1=9.806×104+815.7×9.807x2=114.06×103(Pa) 在截面2处(p+pgh)2=19.612×104+0=196.12×103(Pa) 由于(p叶pgh)2>(p+Pgh)1,故流体自截面2流向截面1。 元×0.014114060-196120 假设流动为层流,流量为9= =0.00134(m3/s 8×0.04 6 20
Engineering Fluid Mechanics 例 题 6-3 下图所示为内径20mm的倾斜放置的圆管,其中流过密度=815.7kg/m3 、黏 度=0.04Pa·s的流体,已知截面1处的压强p1=9.806104Pa,截面2处的压强 p2=19.612104Pa。试确定流体在管中的流动方向,并计算流量和雷诺数。 解: 20 为了确定流动方向,需要计算截面1和 2处流体总机械能的大小。由于等截面 的管道在1和2处的流速相等,即它们 的动能相等,因而流动的方向决定于 该两处压强势能与位势能之和的大小。 在截面1处 (p+gh)1=9.806104+815.79.8072=114.06103(Pa) 在截面2处 (p+gh)2=19.612104+0=196.12103(Pa) 由于(p+gh)2>(p+gh)1,故流体自截面2流向截面1。 假设流动为层流,流量为 4 π 0.01 114060 196120 0.00134 8 0.04 6 V q − = − = (m3 /s)

工程流体力学 Engineering Fluld Mechanics 例题6-3 0.00134 平均流速ⅴ= =4.25(m/s 元×0.012 雷诺数Re=pvd 815.7×4.25×0.02 =1735 4 0.04 由于Re<2000,以上计算成立。 倘若R>2000,流动为紊流,以上计算不成立。 21
Engineering Fluid Mechanics 例 题 6-3 21 平均流速 2 0.00134 4.25 π 0.01 = = v 雷诺数 1735 0.04 d 815.7 4.25 0.02 = = = v Re 由于Re<2000,以上计算成立。 倘若Re>2000,流动为紊流,以上计算不成立。 (m/s)