工程流体力学 Engineering Fluld Mechanics 6-4 园管中流体的层流流动 圆管有效截面上的切应力分布 取微体:如图,半径r,长d中心线和轴重合 4受力分析:p,p+ 端的切向力和侧面的法向力在流动方向投影为零。 al 重力pgπr2·dl,无惯性力a= =0 8t 在1方向上的平衡方程 ∑E=0 al 12
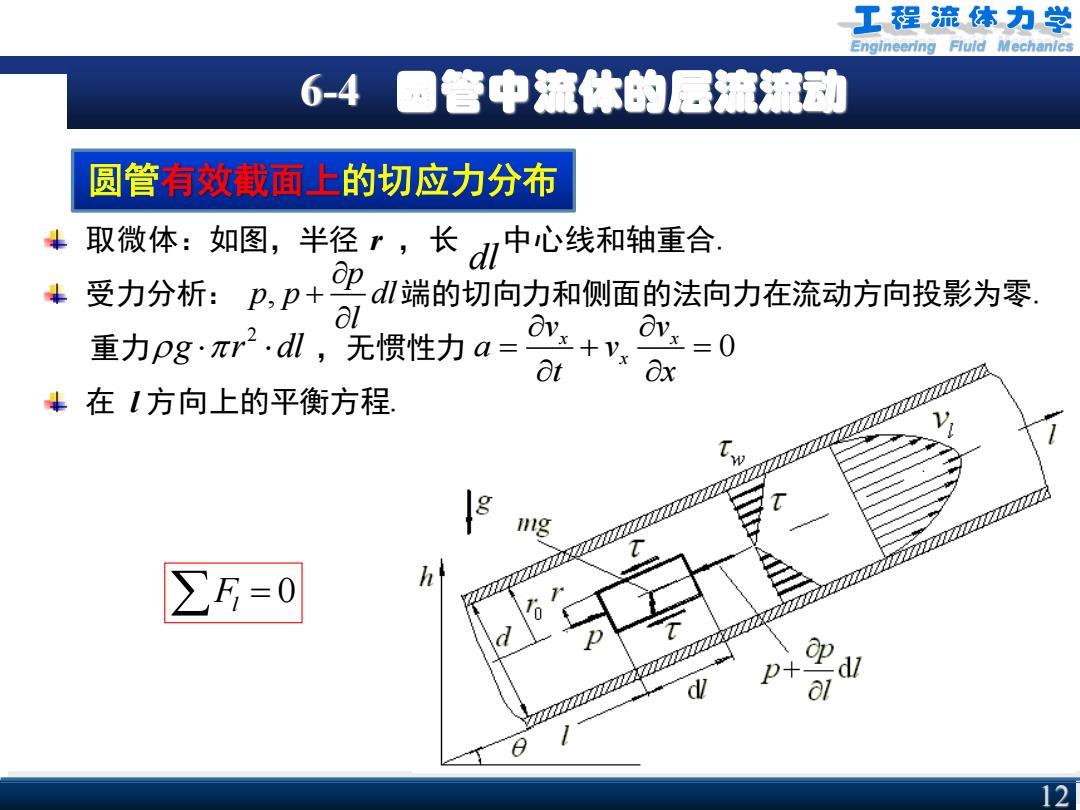
Engineering Fluid Mechanics 6-4 圆管中流体的层流流动 圆管有效截面上的切应力分布 取微体:如图,半径 r ,长 中心线和轴重合. 受力分析: 端的切向力和侧面的法向力在流动方向投影为零. 重力 ,无惯性力 在 l 方向上的平衡方程. dl , p p p dl l + 2 g r dl 0 x x x v v a v t x = + = 0 Fl = 12

工程流体力学 Engineering Fluld Mechanics 6-4 圆管中流体的层流流动 (disin0 al 由:sinO=dh/dl;p+pgh不随r变化 方程两边同除πr2dl得: r d T= 2 (p+pgh) 粘性流体在圆管中作层流流动时,同一 截面上的切向应力的大小与半径成正比 13
Engineering Fluid Mechanics 6-4 圆管中流体的层流流动 2 2 2 ( d ) 2 d d sin 0 p r p r p l r l r l g l − + − − = 由: ; 不随 r 变化 方程两边同除 得: d ( ) 2 d r p gh l = − + p gh + 2 r dl sin d / d = h l 粘性流体在圆管中作层流流动时,同一 截面上的切向应力的大小与半径成正比 13

工程流体力学 Engineering Fluld Mechanics 6-4 @管中流体的层流流动 r d r△p 2dl21 21 水平管 .Ap=p-p2=-dp 没有负号 在管壁上 21 由前述 p= d 2 代入上式得:T。= 8 4
Engineering Fluid Mechanics 6-4 圆管中流体的层流流动 h c = . 2 2 2 r dp r p r p dl l l = − = = 在管壁上 0 2 w r p l = 1 2 = − = − p p p dp 没有负号 由前述 2 2 l v p d = 代入上式得: 2 8 w v = d ( ) 2 d r p gh l = − + 水平管 14

工程流体力学 Engineering Fluld Mechanics 6-4四管中流体的层流流动 层流运动的流速分布 为保证切向应力的值为正,根据牛顿内摩擦定律,得t=一“d山 1 d 代入上式,得dv,= 2 (p+pghrdr 1 d 对积分,得 y=4adp+pghr2+C 当=r时,Y,0,C=-6 d (p+Pgh),代入上式,得 4u dl 1o-r2d 黏性流体在圆管中作层流流动时, V,= 4u dl (p+pgh) 流速的分布规律为旋转抛物面 最大流速为 Vimax d (p+pgh) 4u dl 1 d 平均流速 2 V= 、 2 8μdl (p+pgh)
Engineering Fluid Mechanics 6-4 圆管中流体的层流流动 层流运动的流速分布 为保证切向应力的值为正,根据牛顿内摩擦定律,得 r l d dv = − 代入上式,得 p gh r r l l ( ) d d d 2 1 d v = + 对r积分,得 p gh r C l l = + + 2 ( ) d d 4 1 v 当r=r0时, vl =0, ,代入上式,得 2 0 d ( ) 4 d r C p gh l = − + ( ) d d 4 2 2 0 p gh l r r l + − v = − 黏性流体在圆管中作层流流动时, 流速的分布规律为旋转抛物面 最大流速为 ( ) d d 4 2 0 max p gh l r l v = − + 平均流速 ( ) d d 2 8 1 2 0 max p gh l r l v = v = − +

工程流体力学 Engineering Fluld Mechanics 6-4四管中流体的层流流动 圆管层流流动的流量 圆管中的流量:4,=π。=~% 对于水平圆管 h=c. 哈根一泊肃叶公式 πd4△p 9y= 128uL 16
Engineering Fluid Mechanics 6-4 圆管中流体的层流流动 圆管层流流动的流量 4 2 0 0 d ( ) 8 d V a r q r v p gh l 圆管中的流量: = = − + 对于水平圆管 4 128 V d p q L = ( ) d p p gh dl l + = − 哈根一泊肃叶公式 h c = . 16