
+玩=w+m号 由此可得频率间隔为 △f-f2-f= 2Ts MSK信号的调制指数为 h=△fT,= 2T、 2T, 当取N=1,m=0时,MSK信号的时间波形如图9-6所示。 对第k个码元的相位常数Φ的选择应保证MSK信号相位 在码元转换时刻是连续的。根据这一要求,由式(9.2-2)可以 得到相位约束条件为
T m N T f f S c 1 ) 4 1 ( 4 1 2 − = + = + 由此可得频率间隔为 Δf=f2 -f1 = MSK信号的调制指数为 h=ΔfTs = TS 2 1 0.5 2 1 2 1 2 1 = S = = S S T T T 当取N=1, m=0 时,MSK信号的时间波形如图 9 - 6 所示。 对第k个码元的相位常数φk的选择应保证MSK信号相位 在码元转换时刻是连续的。根据这一要求,由式(9.2 - 2)可以 得到相位约束条件为
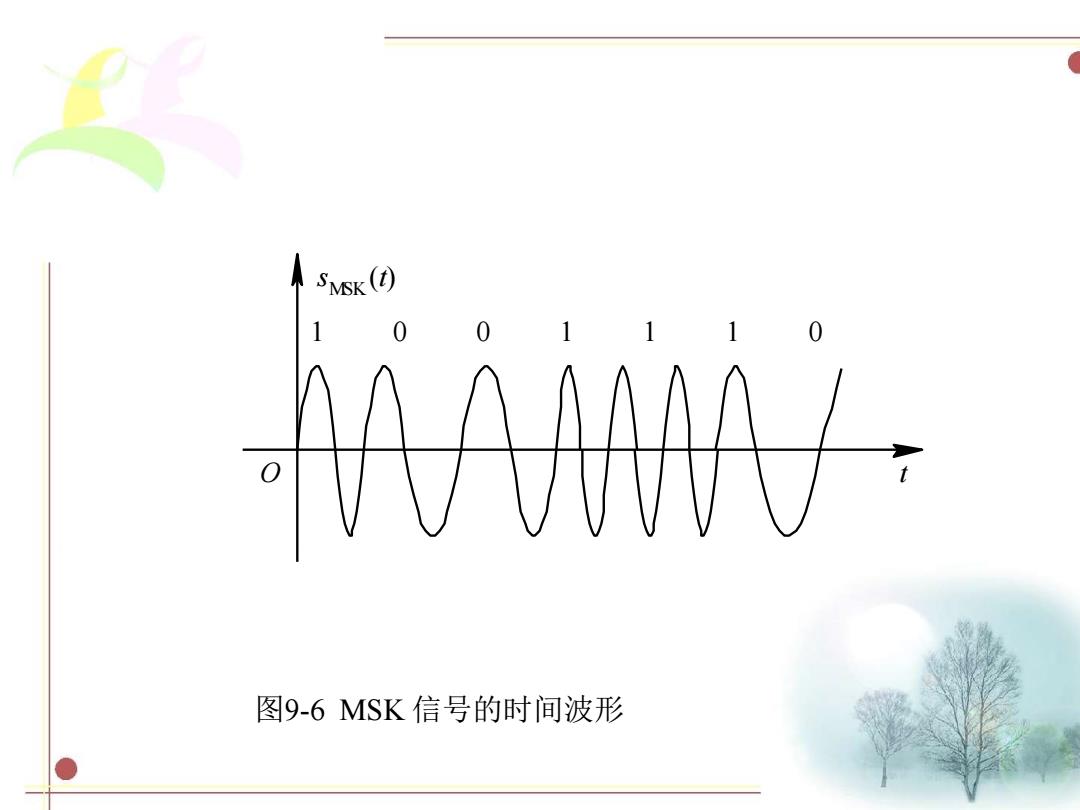
SMK(t) 0 图9-6MSK信号的时间波形
图9-6 MSK 信号的时间波形 1 0 0 1 1 1 0 O t s MSK(t)

9k-1 00aa)写(K-11=9±k-z ak-ak-i akfak-I 式中,若取0的初始参考值o0=0,则 φ=0或士π(模2π)k=0,1,2,… 上式即反映了M$K信号前后码元区间的相位约束关系, 表明MSK信号在第k个码元的相位常数不仅与当前码元的取值 a有关,而且还与前一码元的取值a.1及相位常数pk.1有关
φk=φk-1+(ak-1 -ak ) ( −1)] = 2 [ K K−1 K−1 (k −1) ak=ak-1 ak≠ak-1 式中,若取φk的初始参考值φ0=0,则 φk=0 或 ±π(模2π)k=0, 1, 2, … 上式即反映了MSK信号前后码元区间的相位约束关系, 表明MSK信号在第k个码元的相位常数不仅与当前码元的取值 ak有关,而且还与前一码元的取值ak-1及相位常数φk-1有关

由附加相位函数k()的表示式(9.2-2)可以看出,0(t)是一 直线方程,其斜率为 πakt, 截距为pk。由于ak的取值为士1 2T、 故 π缇分段线性的相位函数。因此,MSK的整个相位路径 2T 是由间隔为Ts的一系列直线段所连成的折线。在任一个码元期 间T,若a=+1,则0(t)线性增加 若a=-l,则6(0线性减 小 。对于给定的输入信号序列{a,相应的附加相位函数 0()的波形如图9-7所示。 对于各种可能的输入信号序列,k()的所有可能路径如图 9-8所示,它是一个从-2π到+2π的网格图
由附加相位函数θk(t)的表示式(9.2 - 2)可以看出,θk (t)是一 直线方程,其斜率为 , 截距为φk。由于ak的取值为±1, 故 是分段线性的相位函数。因此,MSK的整个相位路径 是由间隔为Ts的一系列直线段所连成的折线。在任一个码元期 间Ts,若ak=+1,则θk (t) ;若ak=-1, 则θk (t)线性减 小 。对于给定的输入信号序列{ak},相应的附加相位函数 θk (t)的波形如图 9 - 7 所示。 对于各种可能的输入信号序列,θk(t)的所有可能路径如图 9 - 8 所示,它是一个从-2π到+2π的网格图。 t T a S k 2 t T a S k 2 2 2
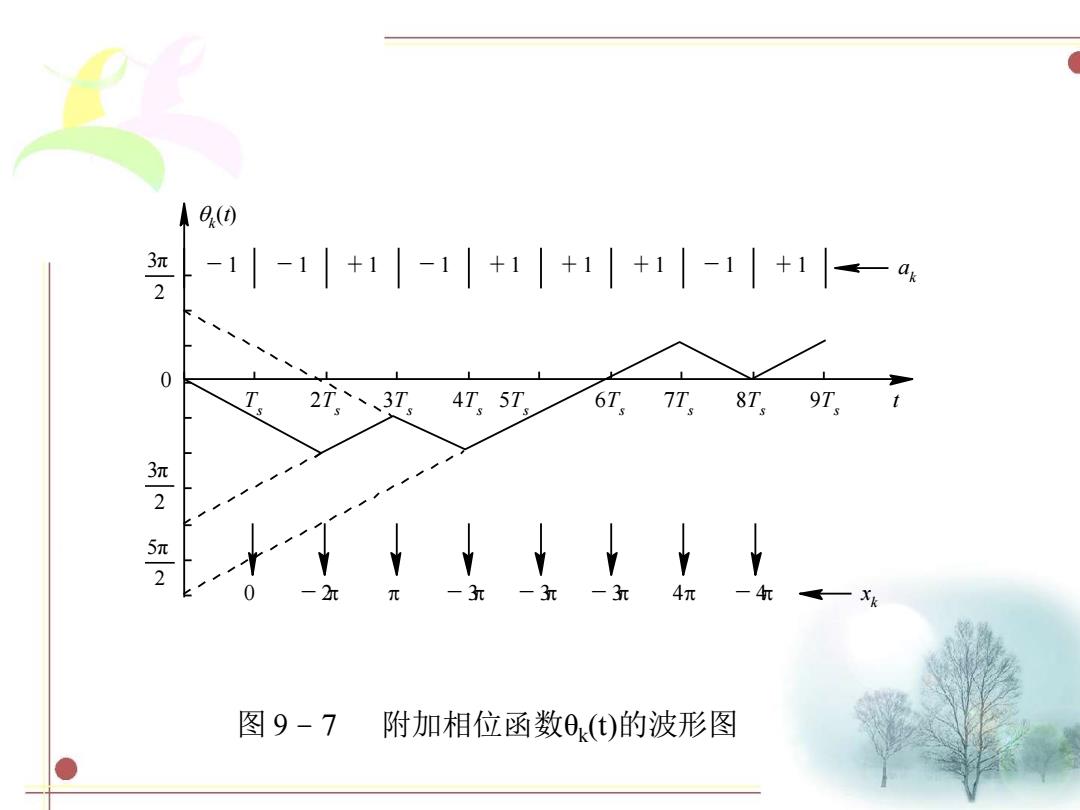
e() -1|-1|+1|-1+1|+1+1-1+1<-a 0 2T,、3T,4T,5T, 6T,7T,8T, 9T 加2 2 -2 一3 -3元 -3 4π 一4红 图9-7 附加相位函数0()的波形图
图 9 – 7 附加相位函数θk (t)的波形图 0 k (t) - 1 - 1 + 1 - 1 + 1 + 1 + 1 - 1 + 1 ak 0 - 2 - 3 - 3 - 3 4 - 4 x k 2Ts Ts 3Ts 4Ts 5Ts 6Ts 7Ts 8Ts 9Ts t 2 3π 2 3π 2 5π