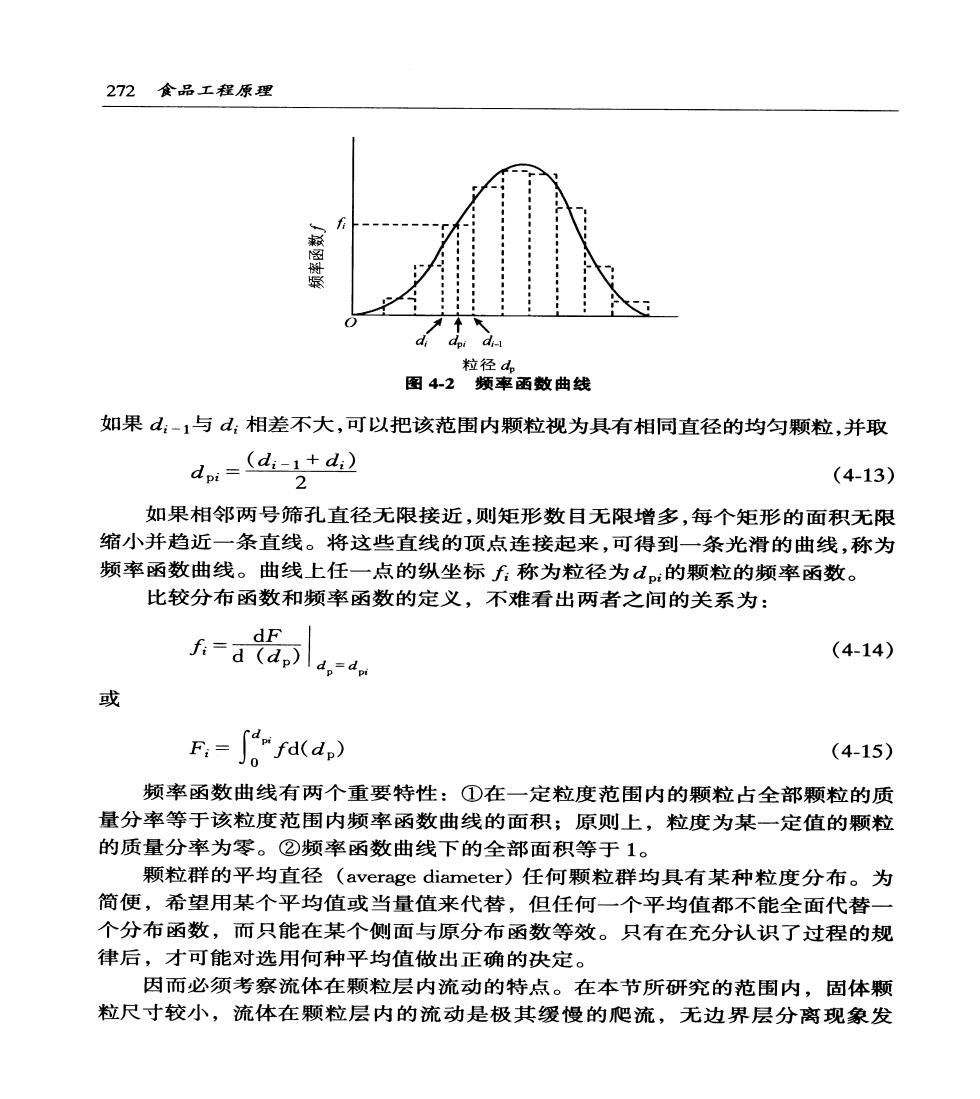
272食品工程原理 d 粒径d 图4-2频率函数曲线 如果d:-1与d:相差不大,可以把该范围内颗粒视为具有相同直径的均匀颗粒,并取 d=(a-2*a2 (4-13) 如果相邻两号筛孔直径无限接近,则矩形数目无限增多,每个矩形的面积无限 缩小并趋近一条直线。将这些直线的顶点连接起来,可得到一条光滑的曲线,称为 频率函数曲线。曲线上任一点的纵坐标f:称为粒径为dp的颗粒的频率函数。 比较分布函数和频率函数的定义,不难看出两者之间的关系为: 万=a指a4 (4-14) 或 F.=fd(d.) (4-15) 频率函数曲线有两个重要特性:①在一定粒度范围内的颗粒占全部颗粒的质 量分率等于该粒度范围内频率函数曲线的面积;原则上,粒度为某一定值的颗粒 的质量分率为零。②频率函数曲线下的全部面积等于1。 颗粒群的平均直径(average diameter)任何颗粒群均具有某种粒度分布。为 简便,希望用某个平均值或当量值来代替,但任何一个平均值都不能全面代替一 个分布函数,而只能在某个侧面与原分布函数等效。只有在充分认识了过程的规 律后,才可能对选用何种平均值做出正确的决定。 因而必须考察流体在颗粒层内流动的特点。在本节所研究的范围内,固体颗 粒尺寸较小,流体在颗粒层内的流动是极其缓慢的爬流,无边界层分离现象发
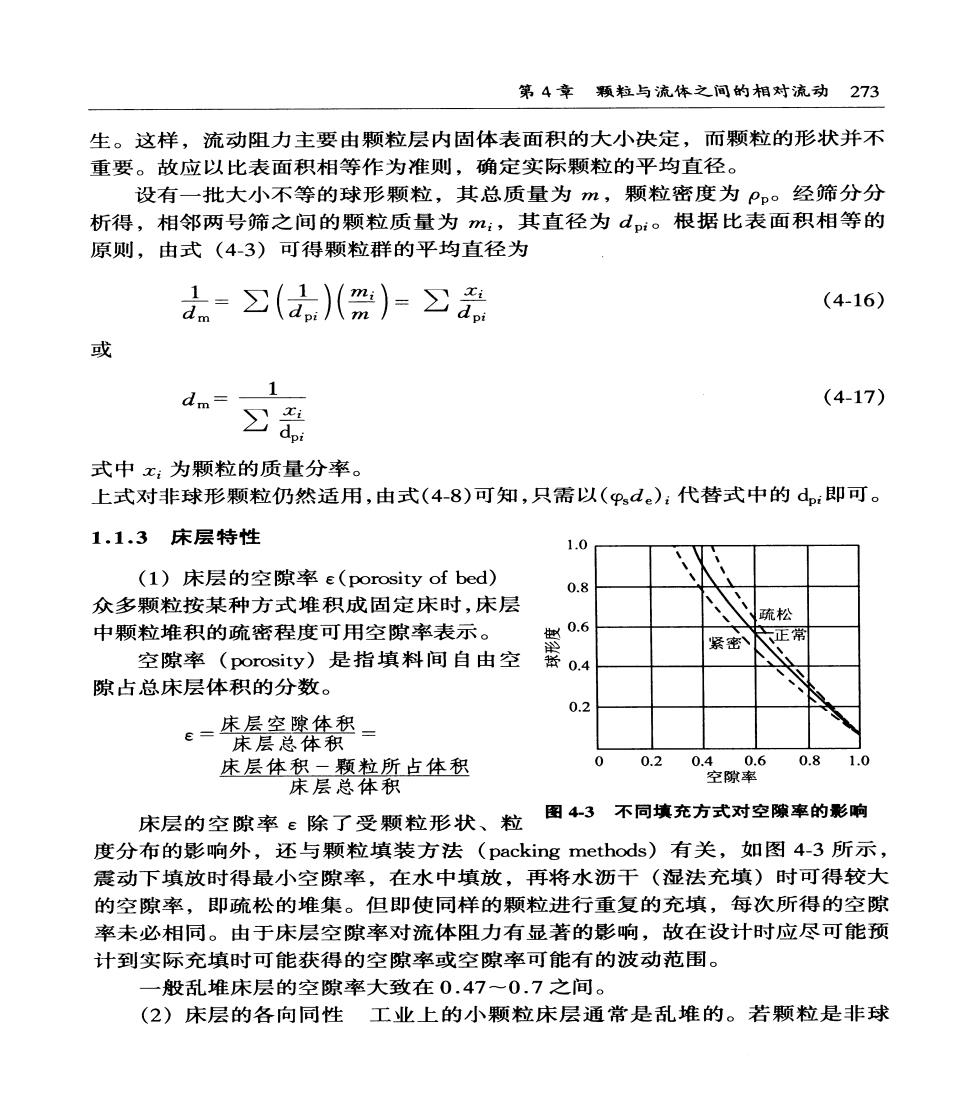
第4章颗粒与流体之间的相对流动273 生。这样,流动阻力主要由颗粒层内固体表面积的大小决定,而颗粒的形状并不 重要。故应以比表面积相等作为准则,确定实际颗粒的平均直径。 设有一批大小不等的球形颗粒,其总质量为m,颗粒密度为P。经筛分分 析得,相邻两号筛之间的颗粒质量为m:,其直径为dp:。根据比表面积相等的 原则,由式(43)可得颗粒群的平均直径为 =(d)(0)=2 (4-16) 或 1 dm= (4-17) 公品 式中x;为颗粒的质量分率。 上式对非球形颗粒仍然适用,由式(4-8)可知,只需以(pd。):代替式中的d,即可。 1.1.3床层特性 1.0 (1)床层的空隙率e(porosity of bed) 0.8 众多颗粒按某种方式堆积成固定床时,床层 疏松 中颗粒堆积的疏密程度可用空隙率表示。 正常 空隙率(porosity)是指填料间自由空 隙占总床层体积的分数。 02 e=床层空啤体积= 床层总体积 床层体积一颗粒所占体积 0 0.8 1.0 床层总体积 床层的空隙率e除了受颗粒形状、粒 图43不同填充方式对空隙率的影响 度分布的影响外,还与颗粒填装方法(packing methods)有关,如图4-3所示 震动下填放时得最小空隙率,在水中填放,再将水沥干(湿法充填)时可得较大 的空隙率,即疏松的堆集。但即使同样的颗粒进行重复的充填,每次所得的空隙 率未必相同。由于床层空隙率对流体阻力有显著的影响,故在设计时应尽可能预 计到实际充填时可能获得的空隙率或空隙率可能有的波动范围。 一般乱堆床层的空隙率大致在0.47一0.7之间。 (2)床层的各向同性工业上的小颗粒床层通常是乱堆的。若颗粒是非球

274食品工程原理 形,各颗粒的定向应是随机的,从而可以认为床层是各向同性的。 各向同性的一个重要特点:床层横截面上可供流体通过的空隙面积(即自由 截面)与床层截面之比在数值上等于空隙率e。 实际上,壁面附近的空隙率总是大于床层内部。因阻力较小,流体在近壁处 的流速必大于床层内部,这种现象称为壁效应(wall effect)。对于直径D较大的 床层,近壁区所占的比例较小,壁效应的影响可忽略,如圆简形床层的直径为 颗粒直径的1020倍以上,壁效应可以忽略;而当床层直径与颗粒直径之比号。 较小时,壁效应的影响则必须考虑。 (3)床层的比表面(specific surface of bed)单位床层体积(不是颗粒体 积)具有的颗粒表面积称为床层的比表面αB。如果忽略因颗粒相互接触而使裸 露的颗粒表面减少,则aB与颗粒的比表面a之间有如下关系: aB=a (1-e) (4-18) 床层通道特性固体颗粒堆积所形成的孔道的形状是不规则的、细小曲折 的。许多研究者将孔道视作流道,并将其简化成长度为L。的一组平行细管,并 规定:①细管的内表面积等于床层颗粒的全部表面;②细管的全部流动等于颗粒 床层的空隙容积。则这些虚拟细管的当量直径d。为: 流道的截面积 山。=流体流动清的调边 则 流道容积 对球形颗粒而言,球形颗粒的直径为4。,体积为元号,表面积为。若 床尽的高度为L,圆形床宋层的直径为D,固体颗粒床层的体积即为元D华;若 床层的空隙率为€,则床层中球形颗粒的个数为: x D2L (1-e) 4 这些球形颗粒所具有的总表面积为:

第4章颗粒与流体之间的相对流动275 x D2L (1-e) A= .xd3=GxD2L (1-e) 4dp 由此求得球形颗粒床层的流体流动孔道的当量直径为: 山.一瓷漆装素终整×:=亲本最路集最 = 4πD2Le mD2a=号·ag Edp (4-19) dp 将式(4-3)代入上式,又有: 4E d.=(1-e)a (4-20) 可见,影响床层通道特性的因素与床层颗粒的特性有关,颗粒的粒度愈小则所 形成的通道数目愈多,通道截面积也愈小,粒度分布愈不均匀和表面愈粗糙的颗粒 所形成的通道就愈不规则,计算流体流动时应折算成当量直径(也称为水力直径)。 1,2流体绕球形颗粒的流动 1.2.1流体绕颗粒的流动状态 设固体颗粒为球形颗粒,若流体为理想流体时,流体内的流线(指这样的曲 线,其每一点处的切线方向即为流体的速度方向)如图4-4(1)所示,A、B两 点的流体处于静止,流速为零,此点称为滞点;而C、D两点的流速则为最大。 当流体为不可压缩流体时,球表面上各点的动能和静压能之和为一常数。因此, 在A、B点处,动能为零,静压能最大;在C、D点处,动能最大,静压能最 小。由于流体无内摩擦力,所以没有摩擦损失。上、下游的流线是完全对称的。 若流体为有粘性的实际流体时,由于粘性的存在,流体在球面附近形成边界 层,其厚度随离前缘距离的增加而增加。流体受到阻力,产生了阻力损失,阻力 损失的大小与流速有关。①如果流体的流速较低,则边界层为滞流边界层 (laminar boundary layer),此时上、下游的流线仍是对称的,与理想流体流动的 不同点仅在于粘性阻力(viscosity resistance)的存在。②如果流体的流速较高, 在前半周,情况仍与①类似,但在后半周,会产生边界层的分离,如图44

276食品工程原理 (2)。边界层分离时,在球体背后形成漩涡,导致能量损失,这一阻力称为形体 阻力(form resistance)。总的阻力为粘性阻力与形体阻力之和,称为局部阻力 (partial resistance)。形体阻力在局部阻力中常占较大比例。③如果流体的流速极 高,则边界层内的流动状态在边界层分离现象发生之前已变为湍流,此时产生边 界层分离的可能性反而不大。 @, (1)理想流体绕流 (2)实际流体绕流 图44流体绕球形颗粒的流动 1.2.2流体绕颗粒流动时的作用力 流体与固体颗粒之间的相对运动可以细分为三种情况:①固体颗粒静止,流体 作绕流:②流体静止,颗粒作沉降运动;③两者都运动但保持移动的相对速度。但 就流体对颗粒的作用力(称为曳力,即流体受到的阻力的反作用力)来讲,只要相对 运动的速度相同,上述三种情形并无本质区别。因此,下面仅讨论第一种情形。 当流体以均匀速度“绕过某静止固 体颗粒时,因相对运动而作用于颗粒上的 曳力(drag force)可分为两类(图4-5)。 一类是剪力在流动方向上的分力总和,称 为表面曳力(surface drag force),若用符 号Fs表示,则Fs=∮twdA sin a;另一 pdA 类为全部表面压力在流动方向上的分压的 总和,称为形体曳力(form drag force),若 1 用符号FF表示,则Fr=中pdA cos a。 流动方向 注意,此形体曳力并不包括浮力。因为当 图45颗粒表面上的曳力 无相对运动时,没有形体曳力,但尚有浮力作用在颗粒上