上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[13]Lecture73-stability analysis in frequency domain 系统稳定性的频域分析

ME369-系统模型、分析与控制 7.3系统稳定性的频域分析 School of Mechanical Engineering ME369-lecture 7.3 Shanghai Jiao Tong University Fall 2015 特征矢量与稳定性 一阶系统 s平面 D(s)=s+p D)=1+ 0 (s=j0) s平面 s平面 D(jo) D(jo jo D(j0) ∠DU -P -P -D 【正实特征根】 【负实特征根】 4∠Djo)=T 4∠Djo)=- 0++o 2 r-0◆+o 2 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 1

1 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering ME369-lecture 7.3 Shanghai Jiao Tong University 7.3 系统稳定性的频域分析 ME369-系统模型、分析与控制 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 特征矢量与稳定性 一阶系统 D s s p ( )   【负实特征根】 【正实特征根】 :0 ( )  2       D j : 0 ( )  2         D j （s j  ）

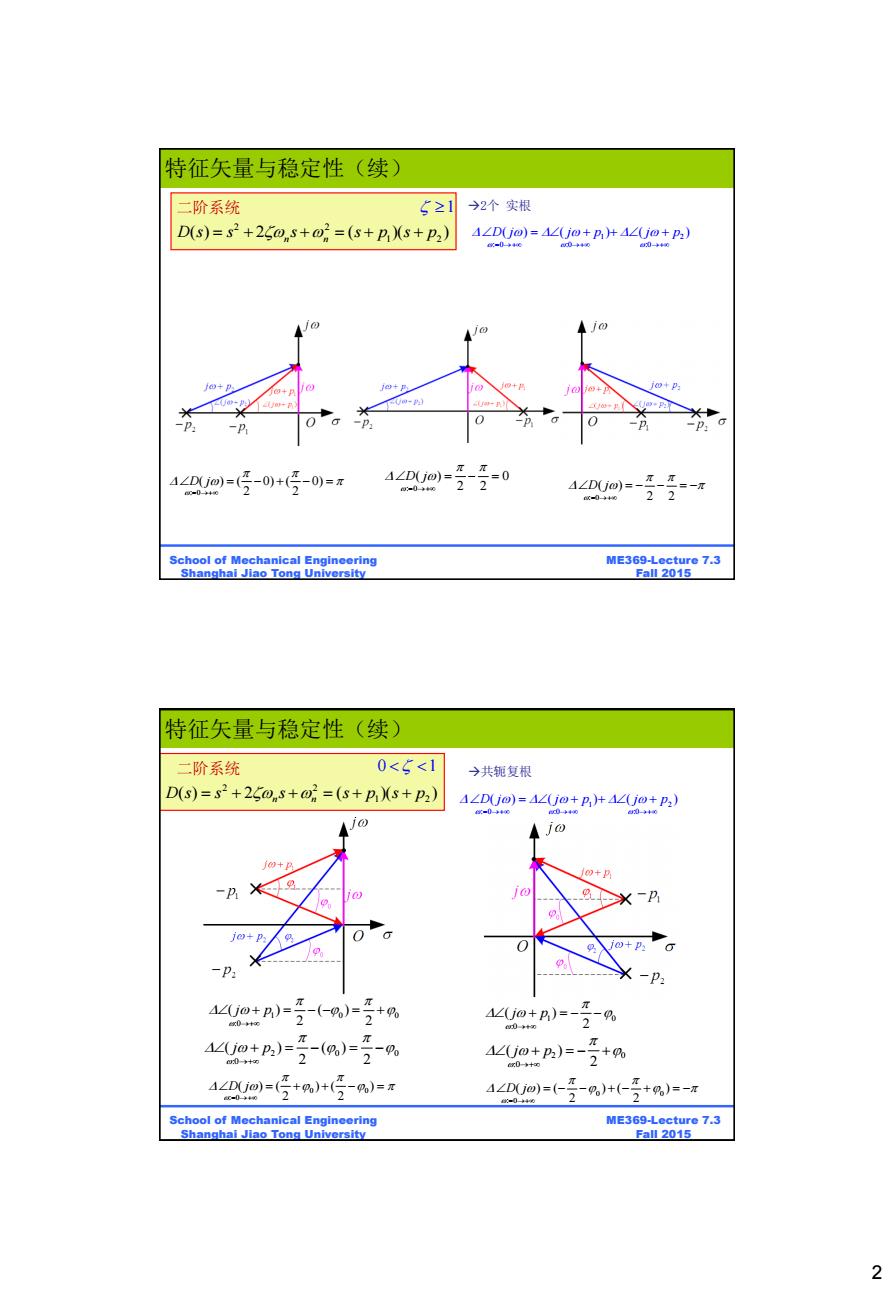
特征矢量与稳定性（续） 二阶系统 521 →2个实根 D(s)=s2+25D,S+o2=(s+Ps+P2) 4∠Djo)=4jo+BHA∠(Uo+P) -0→4 0 jo @+P +P + 1+ -P: ππ 4∠DU)=( -0)+ 2 -0)=π A∠DUj)= -0+e 4∠D(jo)=- =一π 22 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 特征矢量与稳定性（续） 二阶系统 0<5<1 →共轭复根 D(s)=s2+25@s+=(s+pXs+P2) 4∠DUjo)=4∠Uo+B+4∠(jo+P2) =040 040 'u040 j + 10+p -P x-p g入J+P P. X-P 4∠(jo+B)= (%)= π +% A∠j0+乃)=- 0+ 0+汤 2% 4(o+B)= (%) 2 2% 4Uo+Pp2)= 0十0. 2+% A∠Dj=( c-00 +)+（区 2 %)=π =0440 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 2

2 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 二阶系统 2 2 1 2 ( ) 2 ( )( ) D s s s s p s p n n          1 : 0 ( ) ( 0) ( 0) 2 2 D j               : 0 ( ) 0 2 2 D j            : 0 ( ) 2 2 D j               2个 实根 1 2 : 0 :0 :0 D j j p j p ( ) ( ) ( )                     特征矢量与稳定性（续） ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 0 1    1 0 0 :0 ( ) ( ) 2 2 j p                2 0 0 :0 ( ) ( ) 2 2 j p               0 0 : 0 ( ) ( ) ( ) 2 2 D j                 1 0 :0 ( ) 2 j p            2 0 :0 ( ) 2 j p           0 0 : 0 ( ) ( ) ( ) 2 2 D j                    共轭复根 1 2 : 0 :0 :0 D j j p j p ( ) ( ) ( )                     2 2 1 2 ( ) 2 ( )( ) D s s s s p s p n n         特征矢量与稳定性（续） 二阶系统

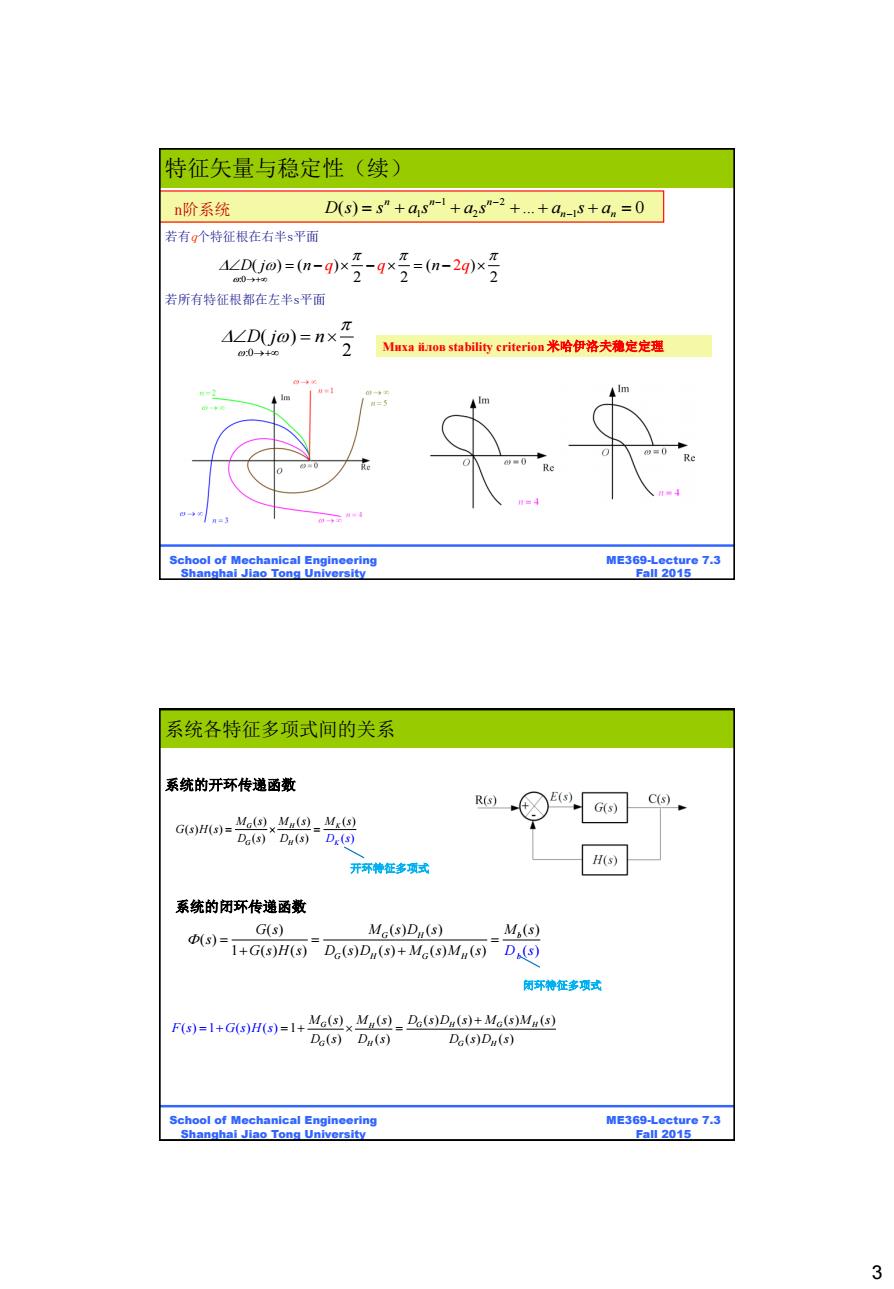
特征矢量与稳定性（续） n阶系统 Ds）=3”+a3-+as"-2++an-3+an=0 若有g个特征根在右半s平面 A/D(jo)=(n-q)xI 0→+a0 =a-240x号 若所有特征根都在左半s平面 ALD(j0)=nX2 00-→+0 Mmxa蓝ostability criterion米哈伊洛夫稳定定理 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 系统各特征多项式间的关系 系统的开环传递函数 R(s) E(s) G(s) C(s) Gs)H(s）= Ma(s)Mu(s)M(s) Da(s)Du(s)De(s) 开环神征多项式 H(s) 系统的闭环传递函数 (s)= G(s) MG(s)Du(s) M,(s) 1+G(s)H(s)Da(s)Du(s)+MG(s)Mn(s)D(s) 闭环神征多项式 Fs=l+GsH句=l+Me(xMn@_Ds)DaS)+Me(s)M包 D(s)D(s) Da(s)Da(s) School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 3

3 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 若所有特征根都在左半s平面 若有q个特征根在右半s平面 :0 ( ) ( ) ( ) 2 2 2 D j n q q n 2q                 :0 ( ) 2 D j n        ( ) ... 1 0 2 2 1   1         n n n n n n阶系统 D s s a s a s a s a Миха йлов stability criterion 米哈伊洛夫稳定定理 特征矢量与稳定性（续） ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 闭环特征多项式 系统的开环传递函数 系统的闭环传递函数 ( ) ( ) ( ) ( ) ( ( ) ) ( ) ( ) G H K G H K M s M s M s G s H s D s D s D s    ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ) ( ( ) G H b G H G H b G s M s D s M s s G s H s D s M M s D s s D s       ( ) ( ) ( ) ( ( ) 1 ( ) ) ( ) 1 ( ) ( ) ( ) ( ( ) ( ) ) G G H G H H G H G H M s D s D s M s M s M s D s D s D s D s F s G s H s        系统各特征多项式间的关系 开环特征多项式

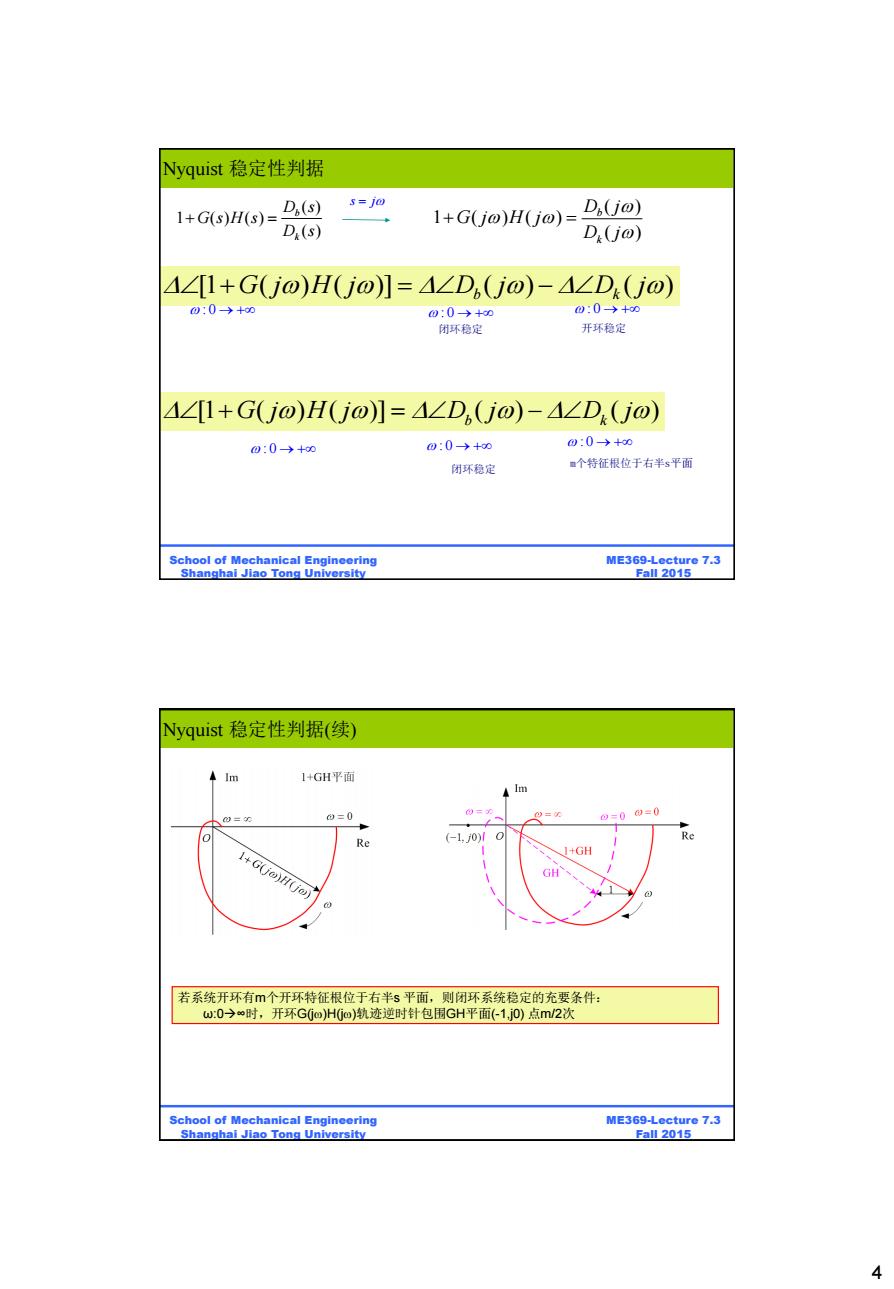
Nyquist稳定性判据 D,(s) 3=j0 1+G(s)H(s)= 1+G(jo)H(U@)= D,(jo) D(s) D(jo) A∠1+G(jo)H(jo)]=4∠D(jo)-A∠D(jo) 0:0→+0 0:0→+0 0:0→+0 闭环稳定 开环稳定 4∠1+G(jo)H(jo)]=△∠D,(jo)-4∠D(Uo) 0:0→+0 0:0→+0 0:0→+0 闭环稳定 ■个特征根位于右半s平面 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 Nyquist稳定性判据（续） ◆lm 1+GH平面 A Im 0=0 =0 ”= =001=0 Re Re 1+GH 1+G(jo GH 若系统开环有m个开环特征根位于右半s平面，则闭环系统稳定的充要条件： w:0→∞时，开环G(o)Ho)轨迹逆时针包围GH平面(-1，j0)点m/2次 School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 4

4 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [1 ( ) ( )] ( ) ( )              G j H j D j D j b k ( ) ( ) 1 ( ) ( ) D s D s G s H s k b   ( ) ( ) 1 ( ) ( )     D j D j G j H j k b   闭环稳定 开环稳定 s j    :0   Nyquist 稳定性判据  :0    :0   [1 ( ) ( )] ( ) ( )              G j H j D j D j b k m个特征根位于右半s平面  :0    :0    :0   闭环稳定 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Nyquist 稳定性判据(续) 若系统开环有m个开环特征根位于右半s 平面，则闭环系统稳定的充要条件： ω:0∞时，开环G(j)H(j)轨迹逆时针包围GH平面(-1,j0) 点m/2次

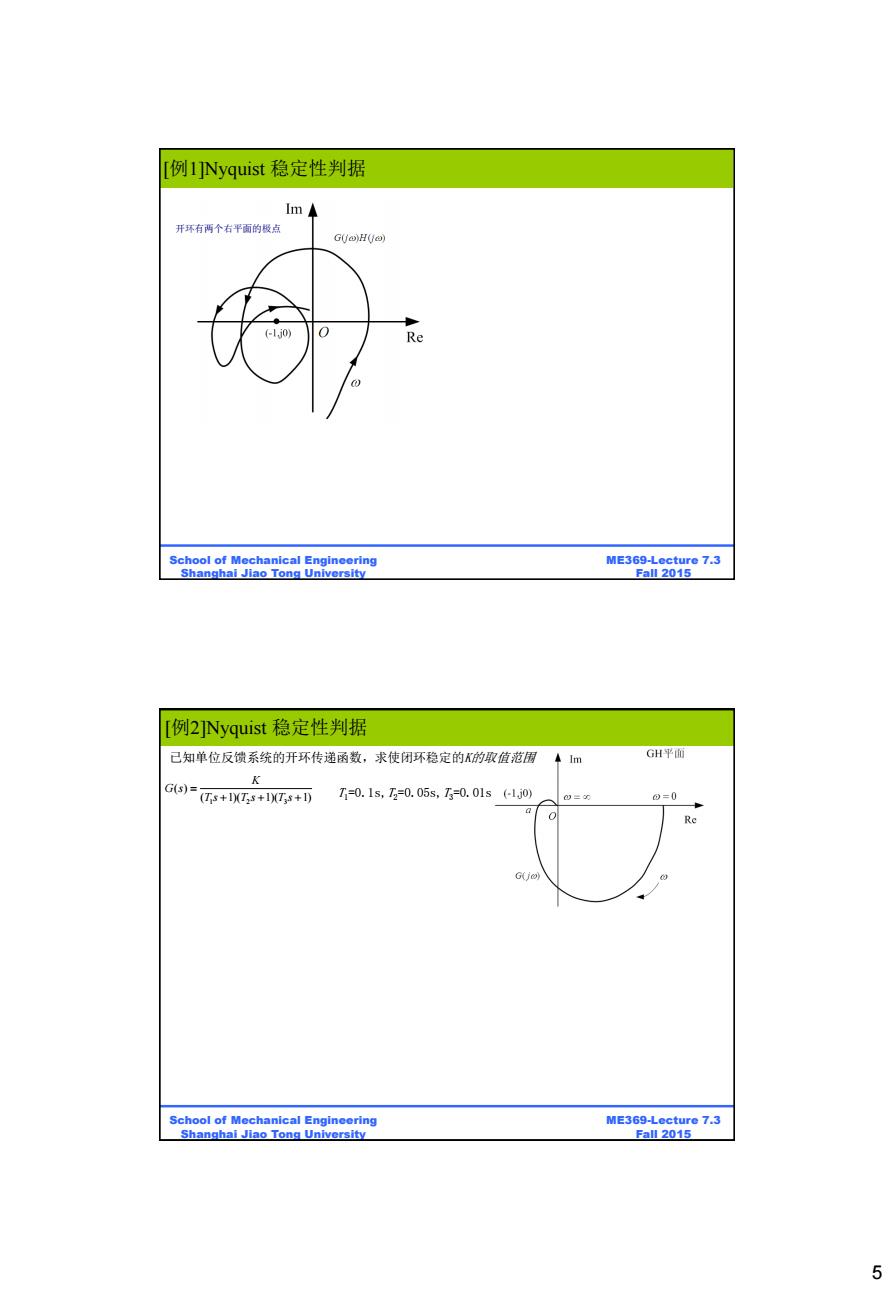
T例1 Nyquist稳定性判据 Im◆ 开环有两个右平面的极点 G(o)H() 10) 0 Re School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 [例2 Nyquist稳定性判据 已知单位反馈系统的开环传递函数，求使闭环稳定的的取值范围 GH平面 G)严p+lXI+T+ T=0.1s,T2=0.05s,T=0.01s1j0) a)=0 0=0 Re G(jw) School of Mechanical Engineering ME369-Lecture 7.3 Shanghai Jiao Tong University Fall 2015 5

5 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 开环有两个右平面的极点 [例1]Nyquist 稳定性判据 ME369-Lecture 7.3 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 1 2 3 ( ) ( 1)( 1)( 1) K G s T s T s T s     已知单位反馈系统的开环传递函数，求使闭环稳定的K的取值范围 T1=0.1s,T2=0.05s,T3=0.01s [例2]Nyquist 稳定性判据