上海交通大学：《系统模型、分析与控制 Modeling、Analysis and Control》课程教学资源[08]Lecture62-Stability 系统稳定性

ME369-系统模型、分析与控制 6.2系统稳定性 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 T引例1]稳定性(Stability)定义 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 1

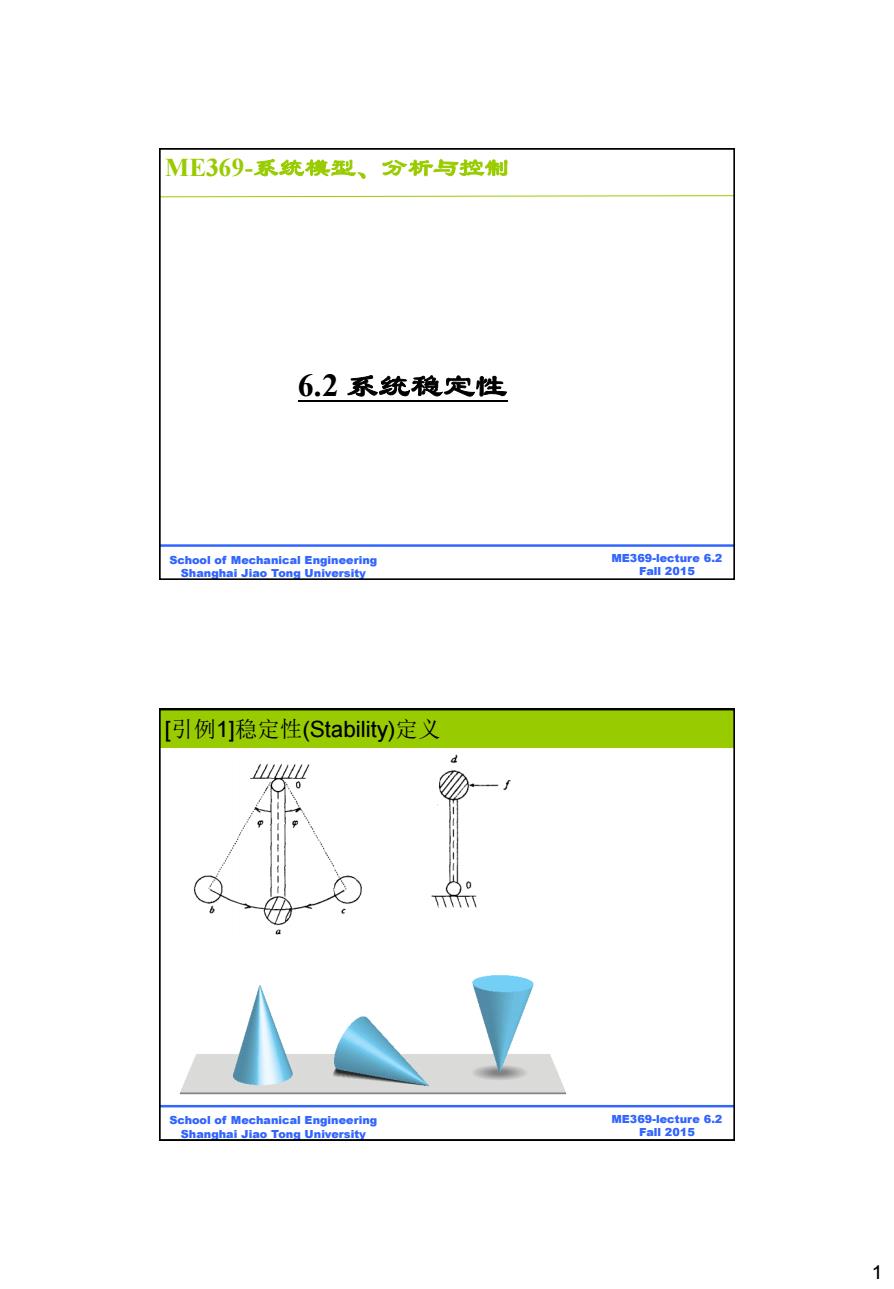
1 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 6.2 系统稳定性 ME369-系统模型、分析与控制 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [引例1]稳定性(Stability)定义

[引例2]稳定性定义 Tacoma narrows bridge 华盛顿州塔科马峡谷的大桥 Built July Ist,1940 Nov7h,1940 5 seconds School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fal12015 引例3稳定性定义 R(s) E(s) G(s) C(s) C(s)=_ G(s) R(s)1-G(s)H(s) H(s) G(s)=5H(s)=0.1 ()=1 G(s)=10 H(s)=0.1 r)=1 G(s)=5 H(s)=0.2 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 2

2 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Tacoma narrows bridge 华盛顿州塔科马峡谷的大桥 Built : July 1st ,1940 Nov 7th , 1940 [引例2]稳定性定义 5 seconds ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) ( ) ( ) 1 ( ) ( ) C s G s R s G s H s   G s( ) 5  H s( ) 0.1  r t( ) 1  G s( ) 10  H s( ) 0.1  G s( ) 5  H s( ) 0.2  r t( ) 1  [引例3]稳定性定义

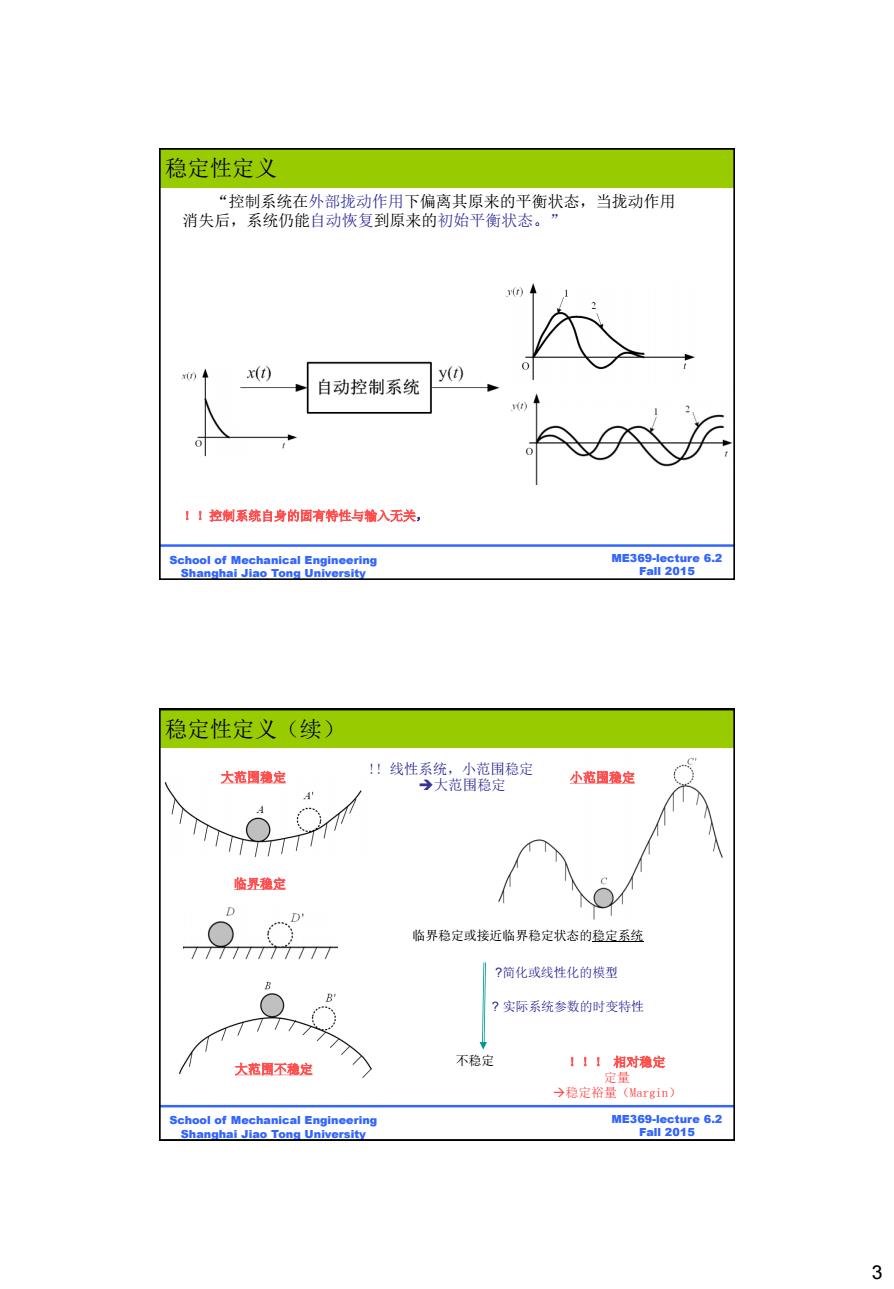
稳定性定义 “控制系统在外部拢动作用下偏离其原来的平衡状态，当拢动作用 消失后，系统仍能自动恢复到原来的初始平衡状态。” v(r) x(t) y(t) 自动控制系统 11控制系统自身的固有特性与输入无关， School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 稳定性定义（续） 大花圆稳定 !线性系统，小范围稳定 →大范围稳定 小范围稳定 临界稳定 D D 临界稳定或接近临界稳定状态的稳定系统 7TT777T777T ?简化或线性化的模型 ？实际系统参数的时变特性 77 大花圆不糖定 入 不稳定 1【1相对稳定 定量 →稳定裕量(Margin) School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 3

3 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University “控制系统在外部拢动作用下偏离其原来的平衡状态，当拢动作用 消失后，系统仍能自动恢复到原来的初始平衡状态。” ！！控制系统自身的固有特性与输入无关， 稳定性定义 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 大范围稳定 小范围稳定 !! 线性系统，小范围稳定 大范围稳定 大范围不稳定 临界稳定 ！！！ 相对稳定 定量 稳定裕量（Margin） ?简化或线性化的模型 ? 实际系统参数的时变特性 不稳定 临界稳定或接近临界稳定状态的稳定系统 稳定性定义（续）

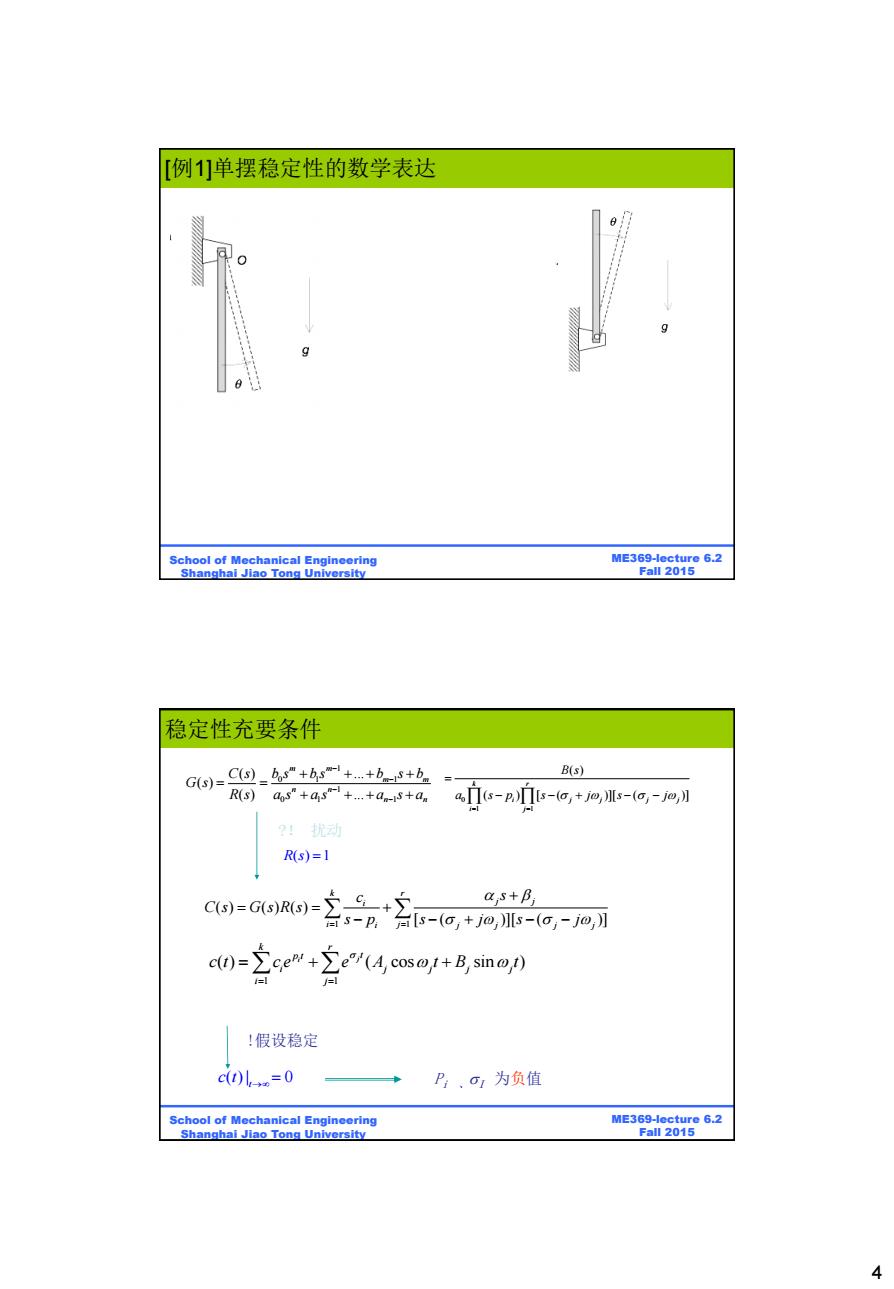
[例1]单摆稳定性的数学表达 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 稳定性充要条件 G6)=C-+hs-++b8+b B(s) R(s)aos"+as"+.+as+a a广s-p-o,+jo,s-(o,-jm,】 2!动 R(s)=1 a,s+B C()-G(S)R(s)ps=(a.+io.s=(a.-o c()(cos+B,sin) 人 !假设稳定 c()l=0 P:、o1为负值 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 4

4 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University [例1]单摆稳定性的数学表达 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Pi 、I 为负值 !假设稳定 1 1 ( ) ( ) ( ) [ ( )][ ( )] k r j j i i j i j j j j c s C s G s R s s p s j s j                    1 1 ( ) ( cos sin ) j i k r p t t i j j j j i j c t c e e A t B t           ?！ 扰动 R s( ) 1  ( ) | 0 t c t   0 1 1 ( ) ( ) [ ( )][ ( )] k r i j j j j i j B s a s p s j s j               1 0 1 1 1 0 1 1 ( ) ... ( ) ( ) ... m m m m n n n n C s b s b s b s b G s R s a s a s a s a               稳定性充要条件

稳定性充要条件（续） Iff condition The poles of characteristic equation have negative real part 系统特征方程的根全部具有负实部 D(s)=a(s-p,)s-(G,+j0,s-(o,-jo,】=0 →闭环系统的极点全部在s平面左半部 x平面 0 (稳定) (不稳定) →稳定性与零点无关 School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fal12015 [例1]稳定性充要条件 K 单位反馈系统 G(s)= (K>0,T>0) 求K的取值范围 s(Ts+1) School of Mechanical Engineering ME369-lecture 6.2 Shanghai Jiao Tong University Fall 2015 5

5 ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University Iff condition : The poles of characteristic equation have negative real part 系统特征方程的根全部具有负实部 0 1 1 ( ) ( ) [ ( )][ ( )] 0 K r i j j j j i j D s a s p s j s j                稳定性与零点无关 闭环系统的极点全部在s平面左半部 稳定性充要条件（续） ME369-lecture 6.2 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University ( ) ( 1) K G s s Ts   单位反馈系统 [例1]稳定性充要条件 ( 0, 0) K T   求K的取值范围