
由统计规律可知 >实际损失在(m-6)与(m+6)间的概率为68.27%; (m-26)与(m+26)间的概率为94.45%; (m-36)与(m+36)间的概率为99.73% 理论上上 无论什么保险,只要在纯费率上加三倍标准差,就能充分保 障保险人财务稳定性。 实践中: 强制保险包广泛性②连续性(到期必须续保) K=6/m,足以保证财务稳定性。 自愿保险,由于“逆选择”,K=26/m 危险程度高,且受互灾损失时,K=36/
由统计规律可知: ➢实际损失在(m-б )与(m+б )间的概率为 68.27%; ➢(m-2б)与(m+2б)间的概率为94.45%; ➢(m-3б)与(m+3б)间的概率为99.73% 理论上: 无论什么保险,只要在纯费率上加三倍标准差,就能充分保 障保险人财务稳定性。 实践中: 强制保险①广泛性②连续性(到期必须续保) K=б/m,足以保证财务稳定性。 自愿保险,由于“逆选择”,K=2б/m 危险程度高,且受巨灾损失时,K=3б/m

二、附加费率 根据以往若干年度附加费用构成的实际数额和预 期利润占保险金额比率确定: 附加费用总额 附加费率 ×100% 保险金额总数
二、附加费率 根据以往若干年度附加费用构成的实际数额和预 期利润占保险金额比率确定: 附加费用总额 附加费率 = ╳ 100% 保险金额总数

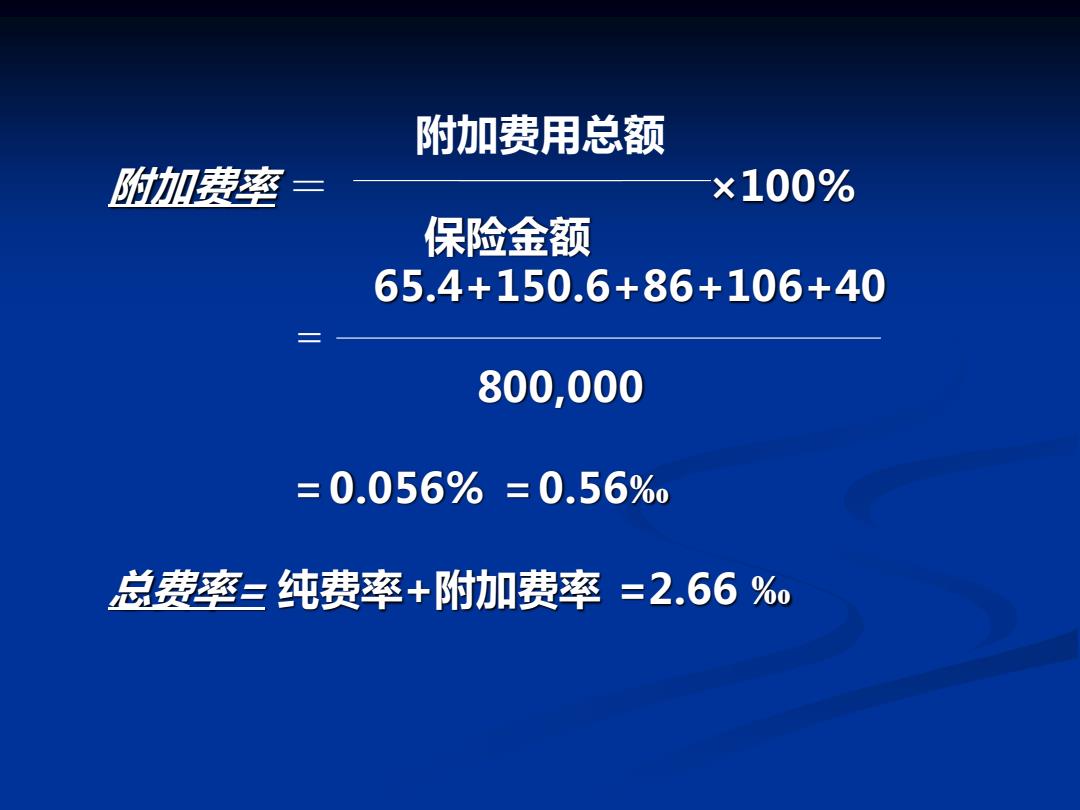
附加费率的计算 例:某财产保险总保险金额为80亿,纯费率为2.1%。, 附加费用有: (1)代理手续费65.4万元 (2)其它管理费150.6万元 (3)职工工资等86万元 (4)营业税收106万元 (5)预期经营利润40万元
附加费率的计算 例:某财产保险总保险金额为80亿,纯费率为2.1‰, 附加费用有: (1)代理手续费65.4万元 (2)其它管理费150.6万元 (3)职工工资等86万元 (4)营业税收106万元 (5)预期经营利润40万元
附加费用总额 附加费率 ×100% 保险金额 65.4+150.6+86+106+40 800,000 =0.056%=0.56%0 总费率三纯费率+附加费率=2.66%
附加费用总额 附加费率 = ×100% 保险金额 65.4+150.6+86+106+40 = 800,000 =0.056% =0.56‰ 总费率= 纯费率+附加费率 =2.66 ‰

三、毛费率 毛费率 =纯费率+ 附加费率 由公式计算出来的毛费率,一般只是承担的某一大类标的 平均数,不能适应某一大类分项业务的风险情况需要。 保额损失率实际上是由统计资料得出的,只能是某一险 种的总损失率,而且实际业务中,根据不同风险要按具体 情况分类制定。 在以往年度统计求得的保额损失率基础上,针对不同标 的,风险性质和风险程度,分项调整,这种调整即级差费 率
三、毛费率 ➢ 毛费率 = 纯费率 + 附加费率 ➢ 由公式计算出来的毛费率,一般只是承担的某一大类标的 平均数,不能适应某一大类分项业务的风险情况需要。 ➢ ∵保额损失率实际上是由统计资料得出的,只能是某一险 种的总损失率,而且实际业务中,根据不同风险要按具体 情况分类制定。 ➢ ∴在以往年度统计求得的保额损失率基础上,针对不同标 的,风险性质和风险程度,分项调整,这种调整即级差费 率