第四章组合逻辑电路 半加器(Half Adder) A S=AB:+AB 函数式 =A⊕B 逻辑图 Ci=AiBi & 曾用符号 HA 国标符号 B A Bi
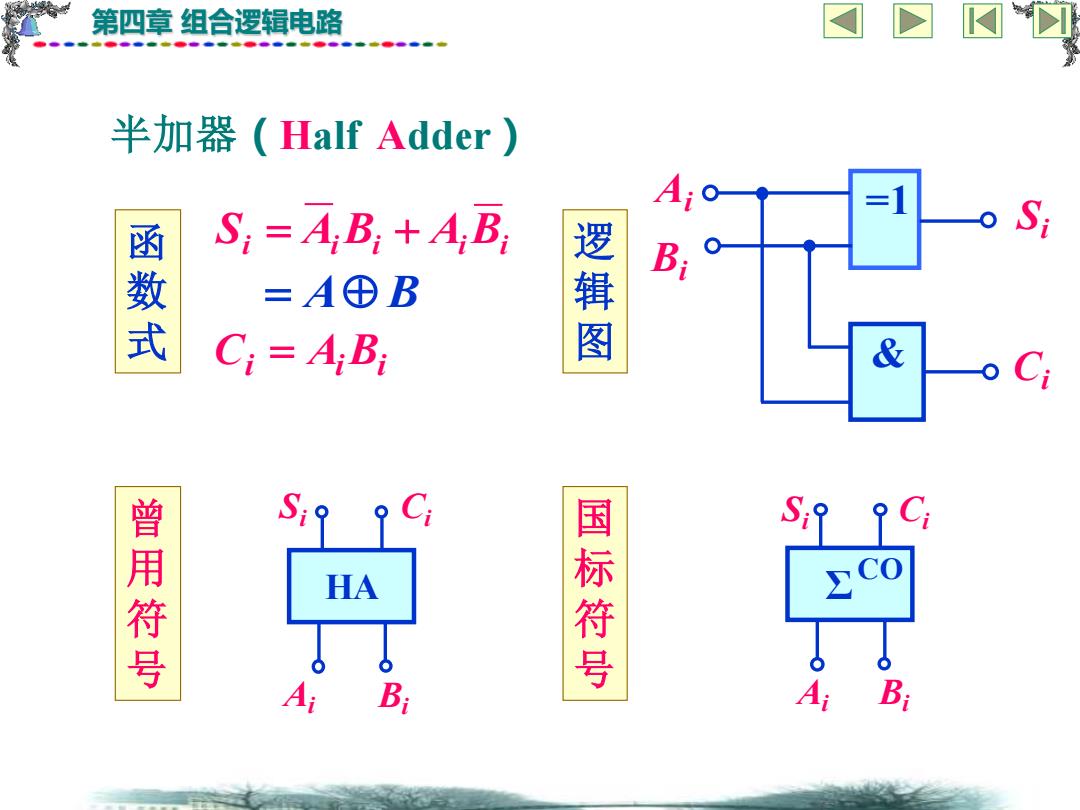
第四章 组合逻辑电路 逻 辑 图 曾 用 符 号 国 标 符 号 半加器(Half Adder) Si & Ai Bi =1 Ci Σ CO Si Ai Bi Ci HA Si Ai Bi Ci Si = Ai Bi + Ai Bi Ci = Ai Bi 函 数 式 = A B
第四章组合逻辑电路 2.全加器(Full Adder ) 两个1位二进制数相加,考虑低位进位。 A;+B:+C:-1(低位进位) 1011 A =S:(和)→C:(向高位进位) 11 0 B +11 低位进位 高位进位一11001 -S A B C Si Ci A B Ci-1 S; C 真值表 0 0 0 0 ■。■08■gg■g等男用图级男8■后原国目8里 1 0 0 0 1 0 标准 S:=AB:Ci+AB:C+A B:Ci+A B;Ci- 与或式 C:=A B:Ci-1+A B;C1+ABCi-+ABiCi
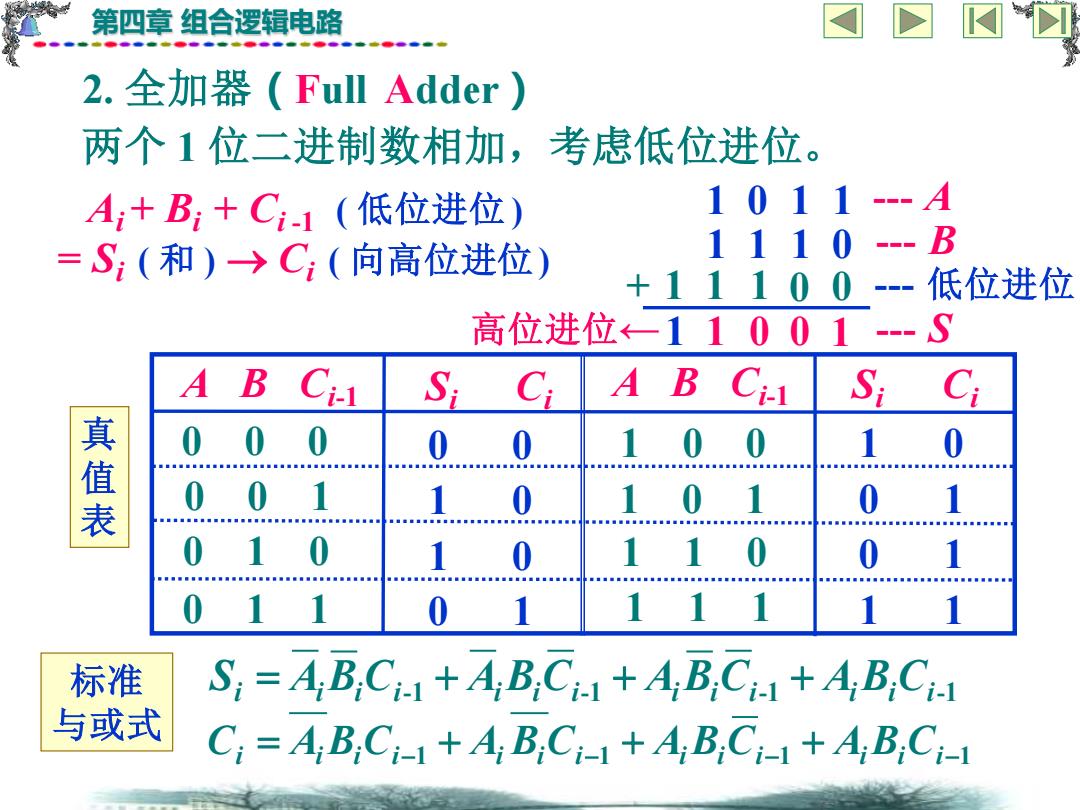
第四章 组合逻辑电路 2. 全加器(Full Adder) 两个 1 位二进制数相加,考虑低位进位。 Ai + Bi + Ci -1 ( 低位进位 ) = Si ( 和 ) → Ci ( 向高位进位) 1 0 1 1 --- A 1 1 1 0 --- B + --- 低位进位 0 1 1 0 0 1 1 1 1 真 值 表 Si = Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 Ci = Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 标准 与或式 A B Ci-1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Si Ci A B Ci-1 Si Ci 0 0 1 0 1 0 0 1 1 0 0 1 0 1 1 1 高位进位← --- S 0

第四章组合逻辑电路 全加器 卡诺图 SBC 001110 A 00011110 0 0 最简与或式 圈 1S=ABC+BE+4BC4BC C=4B:+4C+BC 圈 “0”S,=AB,C1+AB,C+4B,C1+4B,C C=4B +4C+B.C
第四章 组合逻辑电路 卡诺图 全加器 A BC 0 1 00 01 11 10 1 1 1 1 Si A BC 0 1 00 01 11 10 1 1 1 1 Ci 圈 “ 0 ” Si = Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 Ci = Ai Bi + Ai Ci-1 + Bi Ci-1 Si = Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 Ci = Ai Bi + Ai Ci-1 + Bi Ci-1 最简与或式 圈 “ 1

第四章组合逻辑电路 逻辑图 曾用符号 (a)用与门、或门和非门实现 C FA A;Bi Ci- & & &&& && 国标符号 S C B A;BiCi
第四章 组合逻辑电路 逻辑图 (a) 用与门、或门和非门实现 曾用符号 国标符号 Σ CO CI Si Ai BiCi-1 Ci FA Si Ai BiCi-1 Ci & & & & & & & ≥1 1 1 1 Ai Si Ci Bi Ci-1 ≥1
第四章组合逻辑电路 (b)用与或非门和非门实现 S:=A B:Ci-1+AB;Ci+ABCi+A BiCi- C,=A,B,+A,C-1+B,C- Ci ≥1 ≥1 & & Ai B:
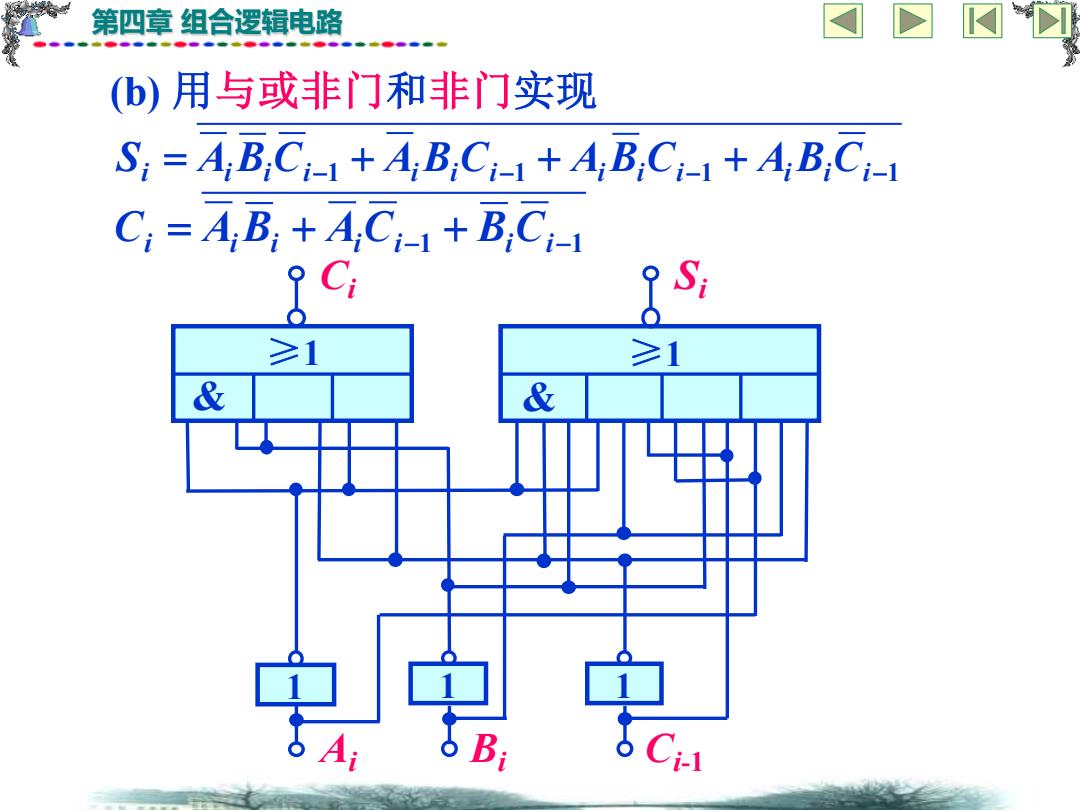
第四章 组合逻辑电路 (b) 用与或非门和非门实现 Si = Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 Ci = Ai Bi + Ai Ci-1 + Bi Ci-1 & ≥1 & ≥1 1 1 1 Ci Si Ai Bi Ci-1