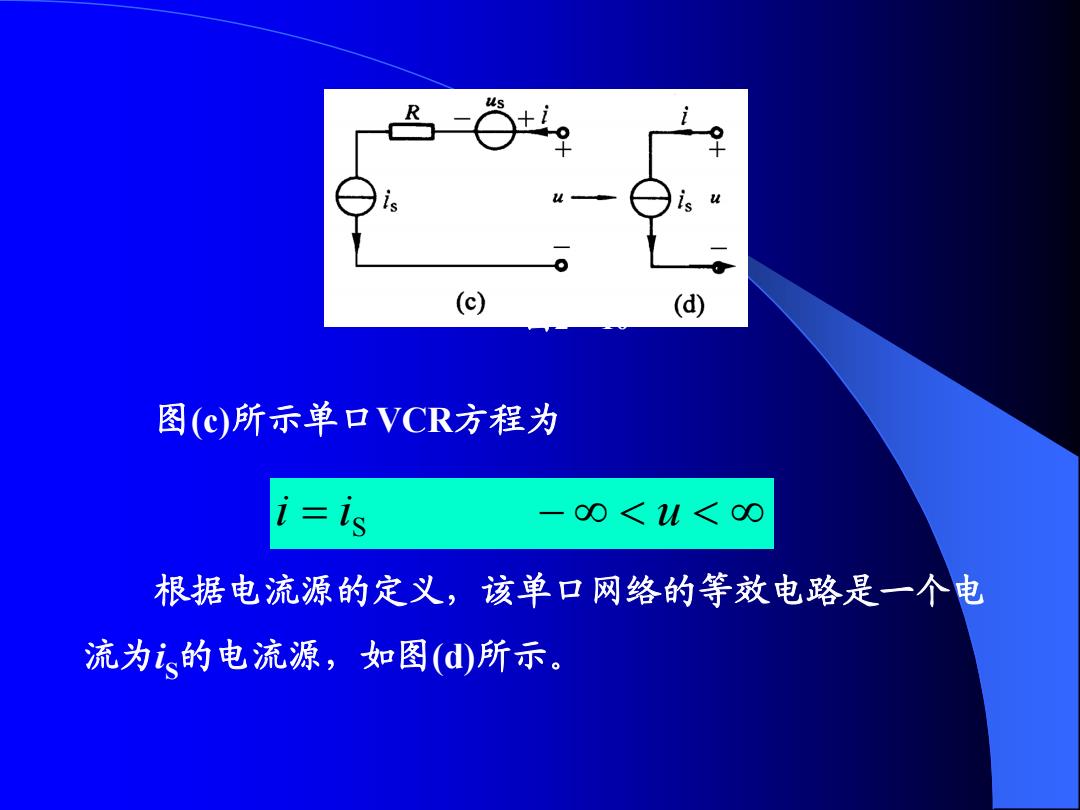
(c) (d) 图(C)所示单口VCR方程为 is i -00<u<o0 根据电流源的定义,该单口网络的等效电路是一个电 流为i、的电流源,如图(d)所示
图(c)所示单口VCR方程为 i i S u 根据电流源的定义,该单口网络的等效电路是一个电 流为i S的电流源,如图(d)所示。 图2-10
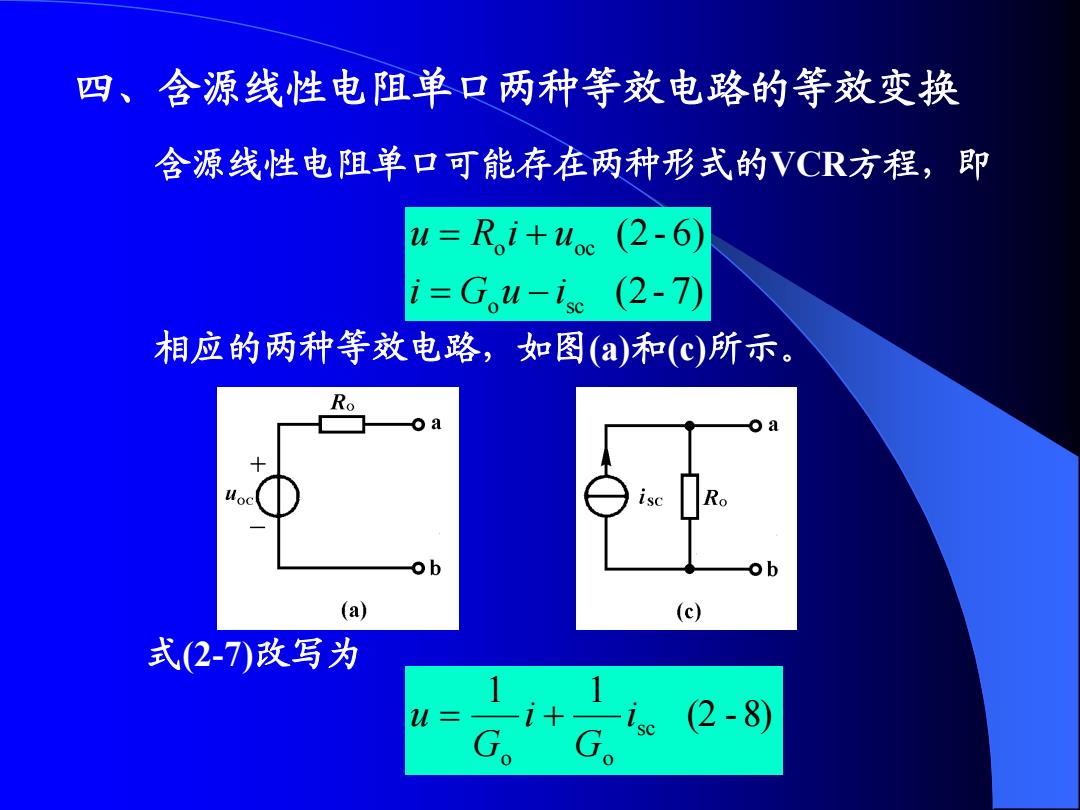
四、含源线性电阻单口两种等效电路的等效变换 含源线性电阻单口可能存在两种形式的VC℉方程,即 u=Ri+uoe (2-6) i=Gw-i。(2-7) 相应的两种等效电路,如图(a和(c)所示。 Ro b (a) (c) 式(2-7)改写为 (2-8)
四、含源线性电阻单口两种等效电路的等效变换 (2- 7) (2- 6) o sc o oc i G u i u R i u 相应的两种等效电路,如图(a)和(c)所示。 (2 - 8) 1 1 sc o o i G i G u 含源线性电阻单口可能存在两种形式的VCR方程,即 式(2-7)改写为

u=Ri+uoe (2-6) 1 (2-8) i=G,u-ic(2-7) 令式(2-6和(2-8)对应系数相等,可求得等效条件为 ue=R,ie或i.= Ro 单口网络两种等效电路的等效变换可用下图表示。 Ro o a 。a Roisc Ro Ro ob ob (a) (b) (c) (d)
o oc oc o sc sc o o 1 R u u R i i G R 或 单口网络两种等效电路的等效变换可用下图表示。 令式(2-6)和(2-8)对应系数相等,可求得等效条件为 (2- 7) (2- 6) o sc o oc i G u i u R i u (2 - 8) 1 1 sc o o i G i G u
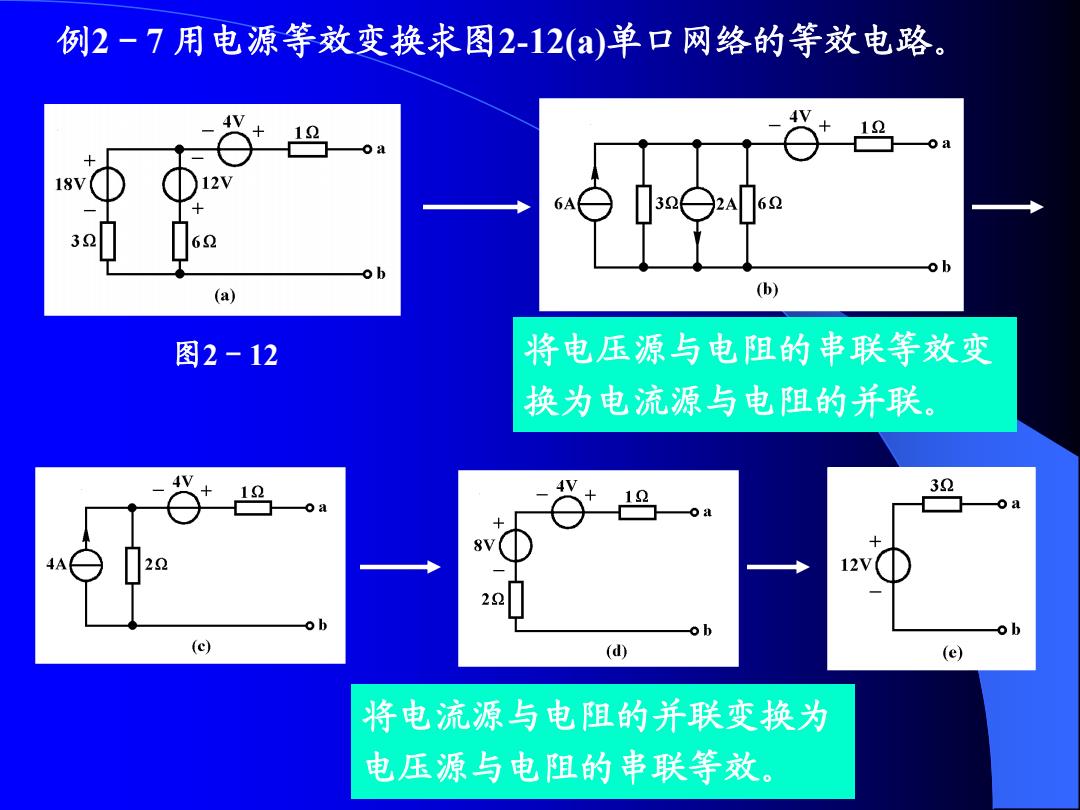
例2-7用电源等效变换求图2-12(a)单口网络的等效电路。 12 -oa ob (a) (b) 图2-12 将电压源与电阻的串联等效变 换为电流源与电阻的并联 32 12 12 (c) (d) (e) 将电流源与电阻的并联变换为 电压源与电阻的串联等效
例2-7 用电源等效变换求图2-12(a)单口网络的等效电路。 将电压源与电阻的串联等效变 换为电流源与电阻的并联。 将电流源与电阻的并联变换为 电压源与电阻的串联等效。 图2-12
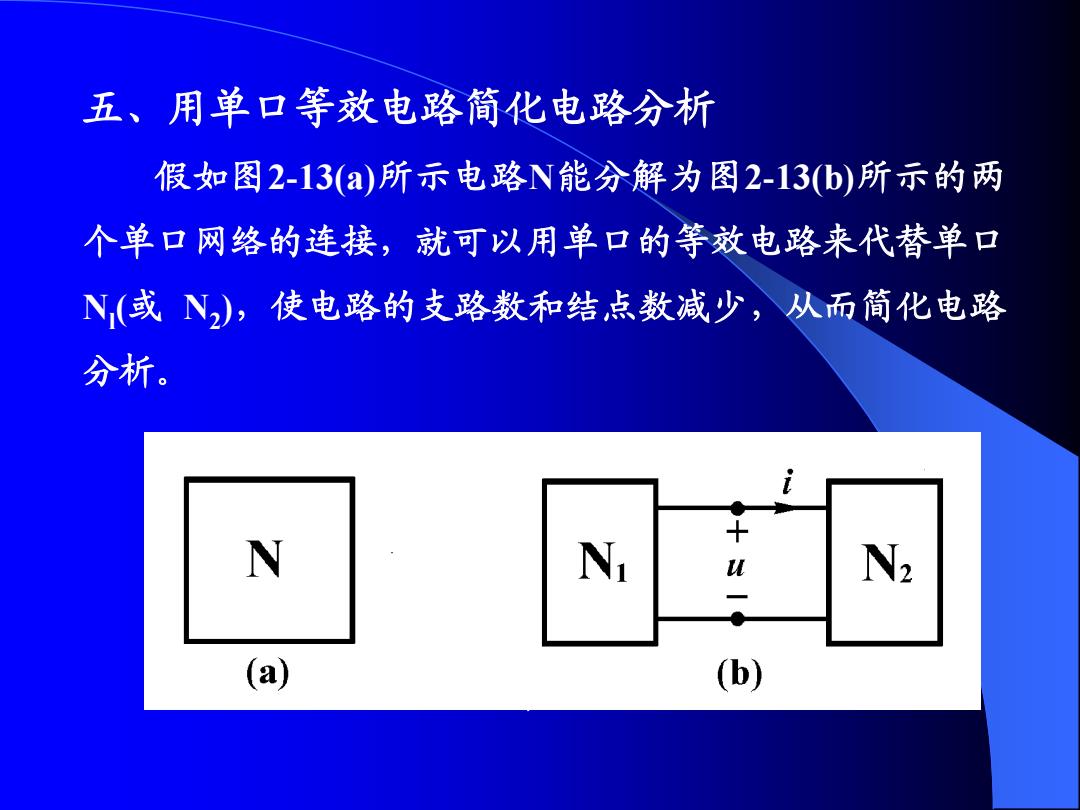
五、用单口等效电路简化电路分析 假如图2-13(a)所示电路N能分解为图2-13(b)所示的两 个单口网络的连接,就可以用单口的等效电路来代替单口 N(或N),使电路的支路数和结点数减少,从而简化电路 分析。 N Ni U N2 (a) (b)
五、用单口等效电路简化电路分析 图2-13 假如图2-13(a)所示电路N能分解为图2-13(b)所示的两 个单口网络的连接,就可以用单口的等效电路来代替单口 Nl (或 N2 ),使电路的支路数和结点数减少,从而简化电路 分析