
四、数学模型及期望均方 (一)数学模型 1.线性模型含义 2.线性模型的意义 (1)固定模型 3.线性模型的分类 2)随机模型 (二)期望均方 (1)顺序性 1.期望均方的含义 (2)组成分 2.期望均方的写法 (3)互作项的去留 3.期望均方的意义 (4)系数的决定 (5)符合选择 (三)线性模型与期望均方的应用

固定模型与随机模型的区别 项目 固定模型 随机模型 试验设计思想 各个处理的平均效应:,=(4-)各个处理的效应x,不是固定的一个 是固定的一个常量。主要研究并常量,而是N(0,σ,)一个随机变量。主 估计处理的效应T 要研究并估计总体变异即方差。 若重复试验则必须包括同样的 若重复试验可从总体中随机抽取参 处理T 试的处理t 统计推断 结论仅在于推断特定的处理 结论将用于推断处理的总体 F测验的实质 H。:t,=0(i=1,2,L,k) H。:4=凸2=L=4 H。:o,2=0 期望均方的符号 K2 02 参数的估计 F测验显著后需进行多重比较 F测验显著后不需进行多重比较,可进 行相关参数计算

随机模型【例】 【例3-2】为研究小麦品种经济性状的数量遗传,随机抽 取90个品种,在田间每品种重复4次,共360个小 区,完全随机设计,得千粒重40.8g,其方差分析列 于下表,试按随机模型对千粒重作出分析。 表90个小麦品种千粒重的方差分析 变异来源DFSS MS f0.01 EMS 品种间 89 8782.5198.6832.04*1.53σ2+4o,2 误差 270831.613.08 62

例 遗传型方差62=g+m0)-0-98.68-3.08=23.90 n 4 广义遗传力(小区为单位) h2- 62 23.90 2+623.9+3.08 =0.836 广义遗传力(品种平均数为单位) 23.90 6+G239+30 =0.969 遗传变异系数 n Gcr-马x10-回1m2 -×100=11.98% x 40.8
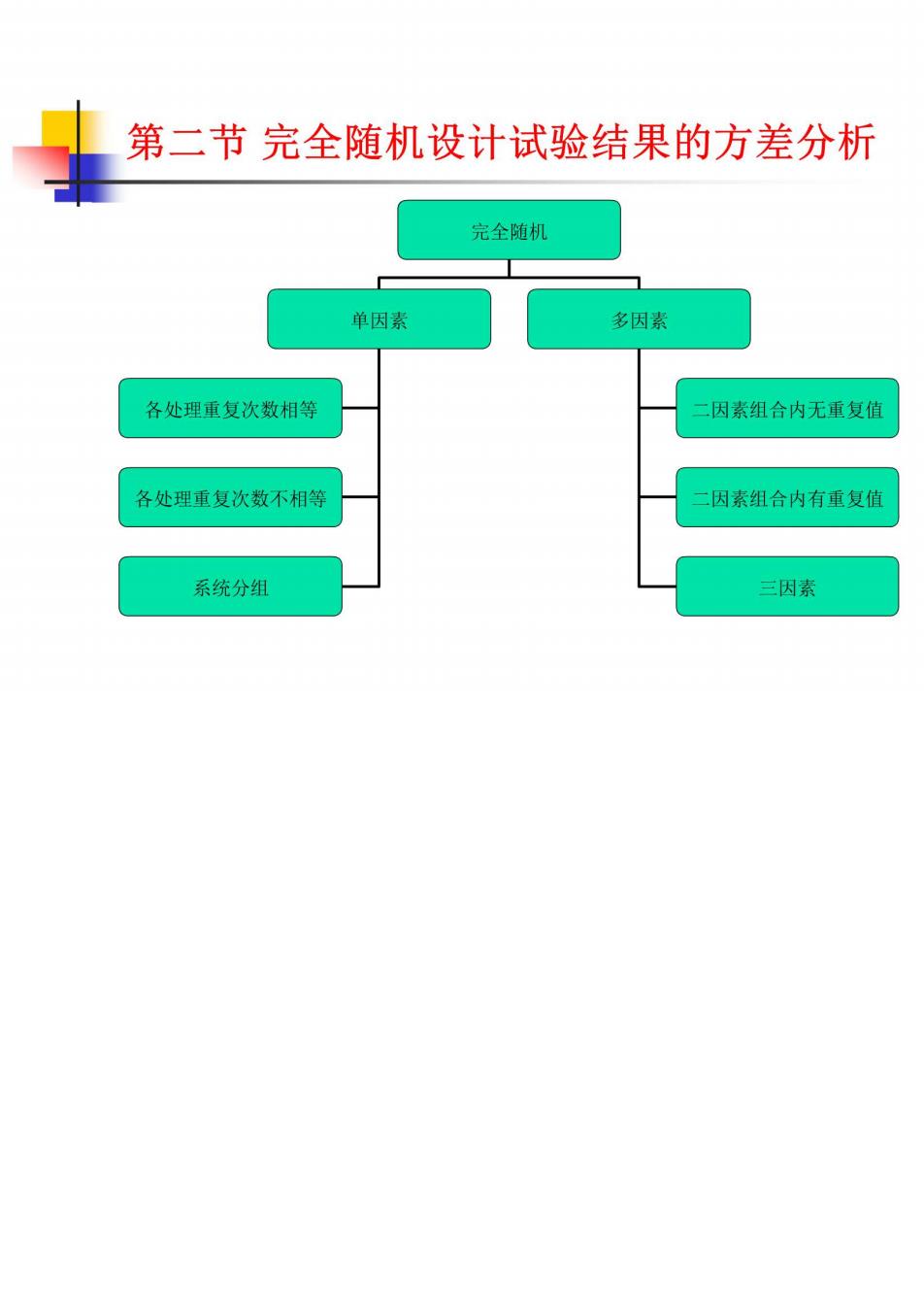
第二节完全随机设计试验结果的方差分析 完全随机 单因素 多因素 各处理重复次数相等 因素组合内无重复值 各处理重复次数不相等 二因素组合内有重复馆 系统分组 三因素