《高分子物理》课程教学资源（书籍教材）胡文兵著《高分子物理导论》，科学出版社，2011

第2章链化学结构的表征 2.1决定高分子物理性质的主要化学结构因素 高分子链结构包括其基本的化学结构（也就是一级结构）以及构象结构（也就 是所谓的二级结构及其在高分子自组装和聚集态结构中的分子构象)。这里，我们 首先介绍化学结构的表征，然后介绍理想无定形链构象的高斯模型处理，接着再介 绍非理想无定形链构象的标度分析处理。嵌段共聚物微相分离态的自组装构象将 在第9章介绍，而高分子结晶态的有序螺旋及其折叠链构象将在第10章介绍。 国际纯粹与应用化学联合会(IUPAC)根据高分子链及其取代基的化学结构 提出了一整套详细的命名方案。但是，在实际的日常学术交流活动中，人们还是喜 欢根据高分子的基本物理行为特点来对其进行命名，例如高密度聚乙烯、发泡聚苯 乙烯、热塑性弹性体、液晶高分子、导电高分子和聚电解质等。这样的命名方式有 利于我们直接把握该高分子的基本结构及其性能特点。 实际上，我们手头一拿到高分子样品，首先需要做的一件事就是要对该样品的 基本物理性质做大致的判断，判断的依据往往是该样品的主要化学结构信息。也 就是说，我们需要对高分子链的化学结构进行必要的描述和表征。那么，对于我们 判断该高分子样品的物理行为特点来说，哪些基本的化学结构信息是至关重要 的呢？ 让我们先来做一个类比，看看我们如何对一块单晶的结构，例如对一颗钻石， 进行描述和表征。首先，单晶的结构单元有内在的对称性，例如碳原子的$杂化 轨道决定了其四面体堆砌结构，分子最稳定的几何构象往往决定了分子间最稳定 堆砌的方位，即晶胞参数的各个轴向之间的夹角；其次，结构单元的堆砌有内在的 周期性，例如碳一碳键长、结构单元之间的相互作用决定了晶胞参数的各个轴距 除了这些表征特定种类晶体共性的内在结构因素之外，每块单晶品还有其个别的外 在特征，主要是晶体的大小、形状和内含的缺陷等。对于一颗钻石来说，这些外在 特征与其市场价值密切相关。按照内在和外在这样两个层次来划分表征一块单晶所 需要的结构因素，有助于我们准确地把握该单晶的基本结构特点及其所决定的性质 我们对高分子样品的描述也可以同单晶类似。首先，高分子的内在特征有链 的半柔顺性，反映分子内寻求最稳定构象的几何结构特点；其次，高分子链有内在 的分子间相互作用的复杂性。主要由于链状分子各向异性的结构特点，分子间相

す౽」 䨫ࡃ႓㐀Ჱ⮱㶕ᒮ ಕႰಔ૓۠Ⴧ倅ܳၽ➖⤳ᕔ䉕⮱ͨ㺮ࡃ႓㐀Ჱ఍㉍ ૓૓倅ܳၽ䨫㐀Ჱ࠲᠙ڣധ᱙⮱ࡃ႓㐀ᲱಉΌᅞ᭜̭㏔㐀ᲱಊВࣷᲱ䆎㐀ᲱಉΌᅞ ᭜᝭䅀⮱ι㏔㐀Ჱڣౕࣷ倅ܳၽ㜗㏱㷲হ㖇䯳ᔮ㐀Ჱ͚⮱ܳၽᲱ䆎ಊ૕䔆䛹ಎ᜾Й 仃اٴϸ㏺ࡃ႓㐀Ჱ⮱㶕ᒮಎ♣ऻϸ㏺⤳ᘠᬍჇᒏ䨫Ჱ䆎⮱倅᫜὎ಸั⤳ಎᣒⱭںϸ ㏺䲋⤳ᘠᬍჇᒏ䨫Ჱ䆎⮱ᴴᏓܳᲽั⤳૕ቹ⃢ڞ㖇➖ᓛⰥܳ⻨ᔮ⮱㜗㏱㷲Ჱ䆎ᄳ ౕすಝ」ϸ㏺ಎ㔹倅ܳၽ㐀ᮣᔮ⮱ᰶᎼ㳧᫸ڣࣷៅऍ䨫Ჱ䆎ᄳౕすಔಓ」ϸ㏺૕ ప䭲㏜㇦̻Ꮑ⩕ࡃ႓㖁वчಉਮ਻ਵਥਧಊᵦᢛ倅ܳၽ䨫ڣࣷःАധ⮱ࡃ႓㐀Ჱ ᣽ܧγ̭᪡ຄ䄓㏳⮱পऺ᫦ᵵ૕ѳ᭜ಎౕ჋䭲⮱ᬒ፥႓ᱜϑ≮≨ߕ͚ಎϧЙ䔅᭜ૉ ⁏ᵦᢛ倅ܳၽ⮱ധ᱙➖⤳㵹ͧ➦◦Გᄦڣ䔈㵹পऺಎҸຯ倅ჳᏓ㖇Ά☜૔ࣾ∎㖇㠜 Ά☜૔☚ൾᕔᑦᕔҀ૔⋟ᮣ倅ܳၽ૔ᄩ⩢倅ܳၽহ㖇⩢㼐䉕ぶ૕䔆ᵤ⮱পऺ᫦ᐼᰶ ݖλ᜾ЙⰡᣒិᤎ䄒倅ܳၽ⮱ധ᱙㐀Ჱڣࣷᕔ㘪➦◦૕ ჋䭲̷ಎ᜾Й᝸๡̭ᠬݝ倅ܳၽᵤ৮ಎ仃اٴ䰭㺮և⮱̭Уθᅞ᭜㺮ᄦ䄒ᵤ৮⮱ ധ᱙➖⤳ᕔ䉕և๔㜡⮱ݑ᫚ಎݑ⮱᫚ӊᢛᒭᒭ᭜䄒ᵤ৮⮱ͨ㺮ࡃ႓㐀ᲱԎᖜ૕Ό ᅞ᭜䄡ಎ᜾Й䰭㺮ᄦ倅ܳၽ䨫⮱ࡃ႓㐀Ჱ䔈㵹ᓲ㺮⮱᣼䔝হ㶕ᒮ૕䗐͵ಎᄦλ᜾Й ݑ᫚䄒倅ܳၽᵤ৮⮱➖⤳㵹ͧ➦◦Გ䄡ಎਗψധ᱙⮱ࡃ႓㐀ᲱԎᖜ᭜㜠ڠ䛺㺮 ⮱এಥ 䃖᜾ЙاٴᲒև̭͗ㆨ℁ಎⰸⰸ᜾Йຯ҂ᄦ̭಄ࢂ⮱ᮣ㐀ᲱಎҸຯᄦ̭䷄䧨ⴠಎ 䔈㵹᣼䔝হ㶕ᒮ૕仃اٴಎࢂ⮱ᮣ㐀Ჱࢂᰶٰڲ⮱ౕᄦ⼝ᕔಎҸຯⷠ࣌ၽ⮱੟ਜ਼ಖ ᱯࡃ 䒕䖀۠Ⴧγڣఈ䲏Ҁളⴹ㐀Ჱಎܳၽᰭ⽠Ⴧ⮱܍҂Ჱ䆎ᒭᒭ۠Ⴧγܳၽ䬡ᰭ⽠Ⴧ ളⴹ⮱᫦Ѻಎࢠᮣ㘋࣯⮱᪝ऱ͗䒡ा͸䬡⮱๦㻿ಟڣ⁎ಎ㐀Ჱࢂ⮱ٰളⴹᰶڲ⮱ౕ ক᱌ᕔಎҸຯⷠ૞ⷠ䩛䪬૔㐀Ჱࢂ͸ٰ䬡⮱Ⱕο҉⩕۠Ⴧγᮣ㘋࣯⮱᪝ऱ͗䒡䌊૕ 䮑γ䔆ψ㶕ᒮ➦Ⴧ⻺ㆨᮣҀڞᕔ⮱ڲౕ㐀Ჱ఍㉍͸ใಎ⃼಄ࢂᮣ䔅ᰶڣ͗ݘ⮱ใ ౕ➦ᒮಎͨ㺮᭜ᮣҀ⮱๔ᄼઽᒏ⟣হڲक़⮱㑧䮤ぶ૕ᄦλ̭䷄䧨ⴠᲒ䄡ಎ䔆ψใౕ ➦ᒮ̻ڣጯ౧ФթჳܴⰥڠ૕ᠶ⚔ڲౕহใౕ䔆ᵤ͑͗ᅯ⁎Გܿܳ㶕ᒮ̭಄ࢂ᝭ᮣ 䰭㺮⮱㐀Ჱ఍㉍ಎᰶߖλ᜾Й۳⶛ౝិᤎ䄒ࢂ⮱ᮣധ᱙㐀Ჱ➦◦ڣࣷ⮱Ⴧ۠᝭ᕔ䉕૕ ᜾Йᄦ倅ܳၽᵤ৮⮱᣼䔝ΌजВहࢂᮣㆨѩ૕仃اٴಎ倅ܳၽ⮱ڲ➦ౕᒮᰶ䨫 ⮱ࡷᴁ䶧ᕔಎࣺܳ᭍ၽڲᄨⅯᰭ⽠ჇᲱ䆎⮱܍҂㐀Ჱ➦◦ಟڣ⁎ಎ倅ܳၽ䨫ᰶڲౕ ⮱ܳၽ䬡Ⱕο҉⩕⮱ฺᱯᕔ૕ͨ㺮⩞λ䨫⟣ܳၽऱाᐯᕔ⮱㐀Ჱ➦◦ಎܳၽ䬡Ⱕ

·12. 高分子物理导论 互作用可以进一步分解为各向同性和各向异性的贡献。正如本书所要展开介绍 的，链的半柔顺性和链间相互作用这两方面的内在特征决定了该品种高分子基本 的物理行为倾向。相应地，每个具体的高分子样品还有其个别的外在特征，主要是 分子质量及其分布、分子拓扑结构和内含的链序列不规整性等。这些外在特征也 与高分子链的物理行为特点密切相关。 把高分子的化学结构特征划分为内外两个层次来进行描述，有助于我们把握 各种结构因素在决定高分子物理行为中所起的相应作用及其地位。通常情况下， 高分子的内在分子结构特征被选择为分子的相互作用能量参数，用来表征高分子 发生物理转变的热力学驱动力，对物理行为的发生起着主要的驱动作用：而代表外 在分子结构特征的分子参数则可以用来表征高分子发生物理转变的限制条件，对 物理行为的发生起到相对比较次要的约束作用。例如，高分子链的各向异性相互 吸引作用通过分子链间的密堆砌驱动高分子链发生结晶。如果高分子链上含有太 多的无规分布的不规整化学序列结构单元，则可能抑制分子链间的密堆砌，阻碍结 晶行为的发生。于是，这样的无规共聚物主要表现出非晶高分子的特点。 下面，我们将对以上高分子链化学结构主要的五个内外表征因素加以进一步 的介绍。 2.2链的半柔顺性 我们可以从单链的理想链模型(idea-chain model)出发，来理解高分子链的半 柔顺性(semi-flexibility)。首先，此理想链模型假定单链足够长，以便我们可以作 近似的统计计算处理。其次，此模型不考虑沿链的长程链单元间相互作用。因此， 这种高分子链也常常被称为虚幻链(phantom chain),或者无扰链(unperturbed chain)。我们从最简单的自由连接链理想模型出发，逐步考虑沿链的短程相互作 用，首先是键角被固定的自由旋转链，然后是内旋转受到阻碍的受阻旋转链，就这 样逐步逼近来描述真实高分子链的半柔顺性。 2.2.1自由连接链 自由连接链(free-jointed chain)就是只考虑链单元之间的连接，暂不考虑每个 连接的角度限制。要表征高分子链的半柔顺性，目前的主要方法是观察高分子无 规线团的尺寸。表征线团尺寸的第一种常见量是高分子链的末端距，其反映在从 高分子链的一端到另一端的矢量R中。假定沿着主链的每个化学键键长为b,这 个末端距矢量是沿着高分子链”个键矢量加和的结果。 R=b1+b2十.+bn= ∑b (2-1)

ο҉⩕जВ䔈̭ₒܳ㼐ͧऱाहᕔহऱाᐯᕔ⮱䉎⡛૕ₐຯ᱙Γ᝭㺮ᆂᐭϸ㏺ ⮱ಎ䨫⮱ࡷᴁ䶧ᕔহ䨫䬡Ⱕο҉⩕䔆͑᫦䲏⮱ڲ➦ౕᒮ۠Ⴧγ䄒৮⻺倅ܳၽധ᱙ ⮱➖⤳㵹ͧիा૕ⰥᏁౝಎ⃼͗ڤҀ⮱倅ܳၽᵤ৮䔅ᰶڣ͗ݘ⮱ใౕ➦ᒮಎͨ㺮᭜ ܳၽ䉕䛼ڣࣷܳጰઽܳၽ᠀᝾㐀Ჱহڲक़⮱䨫Ꮌ݄̺㻱᪡ᕔぶ૕䔆ψใౕ➦ᒮΌ ̻倅ܳၽ䨫⮱➖⤳㵹ͧ➦◦ჳܴⰥڠ૕ ិ倅ܳၽ⮱ࡃ႓㐀Ჱ➦ᒮܿܳͧڲใ͑͗ᅯ⁎Გ䔈㵹᣼䔝ಎᰶߖλ᜾Йិᤎ ऱ⻺㐀Ჱ఍㉍ౕ۠Ⴧ倅ܳၽ➖⤳㵹͚ͧ᝭䊤⮱ⰥᏁ҉⩕ڣࣷౝѺ૕䕇፥ᗲ̸ۢಎ 倅ܳၽ⮱ڲౕܳၽ㐀Ჱ➦ᒮ㷘䔶᠖ͧܳၽ⮱Ⱕο҉⩕㘪䛼࣯᪝ಎ⩕Გ㶕ᒮ倅ܳၽ ࣾ⤳➖⩌䒙अ⮱☚߈႓侞߈ߕಎᄦ➖⤳㵹ͧ⮱ࣾ⩌䊤Ɑͨ㺮⮱侞ߕ⩕҉ಟ㔹А㶕ใ ౕܳၽ㐀Ჱ➦ᒮ⮱ܳၽ࣯݆᪝जВ⩕Გ㶕ᒮ倅ܳၽࣾ⤳➖⩌䒙अ⮱䭽ݣ᲎Уಎᄦ ➖⤳㵹ͧ⮱ࣾ⩌䊤ݝⰥᄦ℁䒰⁎㺮⮱㏓᲌҉⩕૕Ҹຯಎ倅ܳၽ䨫⮱ऱाᐯᕔⰥο ॥ᑂ҉⩕䕇䓴ܳၽ䨫䬡⮱ჳളⴹ侞ߕ倅ܳၽ䨫ࣾ⩌㐀ᮣ૕ຯ᳉倅ܳၽ䨫̷क़ᰶ๗ ็⮱ᬍ㻱ܳጰ⮱̺㻱᪡ࡃ႓Ꮌ݄㐀Ჱࢂٰಎ݆ज㘪ើݣܳၽ䨫䬡⮱ჳളⴹಎ䭨ⶺ㐀 ᮣ㵹ͧ⮱ࣾ૕⩌λ᭜ಎ䔆ᵤ⮱ᬍ㻱ڞ㖇➖ͨ㺮㶕⣝ܧ䲋ᮣ倅ܳၽ⮱➦◦૕ ̸䲏ಎ᜾ЙᄳᄦВ̷倅ܳၽ䨫ࡃ႓㐀Ჱͨ㺮⮱ρ͗ڲใ㶕ᒮ఍㉍ߍВ䔈̭ₒ ⮱ϸ㏺૕ ಕႰಕ૓䨫⮱ࡷᴁ䶧ᕔ ᜾ЙजВϻࢂ䨫⮱⤳ᘠ䨫὎ಸ౱ਾਸਹ਴ੁ႗ਸ਼਽਴ਾ੄੃੅ਸਹੁ౲ࣾܧಎᲒ⤳㼐倅ܳၽ䨫⮱ࡷ ᴁ䶧ᕔ౱੊ਹ੃ਾ႗਺ੁਹ੏ਾਵਾੁਾੋ੐౲૕仃اٴಎₑ⤳ᘠ䨫὎ಸմჇࢂ䨫䋠์䪬ಎВӬ᜾ЙजВ҉ 䓾ѩ⮱㐌䃎䃎ツั⤳૕ڣ⁎ಎₑ὎ಸ̺㔰㭾⇬䨫⮱䪬⼸䨫ࢂٰ䬡Ⱕο҉⩕૕఍ₑಎ 䔆⻺倅ܳၽ䨫Ό፥፥㷘⼝ͧ 㮇Ꭸ䨫 ౱੆਽਴੄ੋ੅੃ਸ਼਽਴ਾ੄౲ಎᝃ 㔲 ᬍឝ䨫 ౱ੌ੄੆ਹ੉ੋੌ੉ਵਹਸ ਸ਼਽਴ਾ੄౲૕᜾Йϻᰭキࢂ⮱㜗⩞䔋ᣒ䨫⤳ᘠ὎ಸࣾܧಎ䔽ₒ㔰㭾⇬䨫⮱ⴚ⼸Ⱕο҉ ⩕ಎ仃اٴ᭜䩛㻿㷘ధჇ⮱㜗⩞᫸䒙䨫ಎ♣ऻ᭜ڲ᫸䒙ऄݝ䭨ⶺ⮱ऄ䭨᫸䒙䨫ಎᅞ䔆 ᵤ䔽ₒ䕩䓾Გ᣼䔝ⱌ჋倅ܳၽ䨫⮱ࡷᴁ䶧ᕔ૕ ౽႖౽႖౼ 㜗⩞䔋ᣒ䨫 㜗⩞䔋ᣒ䨫౱਺੉ਹਹ႗ਿ੅ਾ੄ੋਹਸਸ਼਽਴ਾ੄౲ᅞ᭜ग㔰㭾䨫ࢂ͸ٰ䬡⮱䔋ᣒಎᮯ̺㔰㭾⃼͗ 䔋ᣒ⮱㻿Ꮣ䭽ݣ૕㺮㶕ᒮ倅ܳၽ䨫⮱ࡷᴁ䶧ᕔಎⰛݺc⮱㺮᫦∂᭜㻯ᄌ倅ܳၽᬍ 㻱㏬ఏ⮱ᅧᄥ૕㶕ᒮ㏬ఏᅧᄥ⮱す̭⻺፥㻮䛼᭜倅ܳၽ䨫⮱᱘〜䌊ಎࣺڣౕ᭍ϻ 倅ܳၽ䨫⮱̭〜ݝओ̭〜⮱ⴏ䛼ਣ ͚૕մჇ⇬Ɑͨ䨫⮱⃼͗ࡃ႓䩛䩛䪬ͧਵಎ䔆 ͗᱘〜䌊ⴏ䛼᭜⇬Ɑ倅ܳၽ䨫੄͗䩛ⴏ䛼ߍহ⮱㐀᳉૕ ਣ ಉਵಔ ౵ਵಕ ౵ ૡ ౵ਵ੄ ಉ ૺ ੄ ਾಉಔ ਵਾ ಉಕ႗ಔಊ ૖ಔಕ૖ 倅ܳၽ➖⤳ᄩ䃧

第2章链化学结构的表征 ·13· 如果对足够多的高分子链取平均结果，随机取向的末端距矢量将在结果中相 互抵消掉。因此，我们需要摆脱导致结果抵消的矢量方向信息，用一个标量，即末 端距的平方，叠加起来表征高分子线团的特征尺寸。 R2=∑b·∑b,=b2+2∑∑b,·b (2-2) 1 f=1 由于两个矢量的点积结果主要取决于彼此的夹角Y, b·b:=b2·cosY (2-3) 而自由连接链上的任意两个不同键矢量的夹角可以在0到2π之间均匀分布，导致 其余弦值在一1和1之间均匀分布，足够多这样独立的点积加和的结果就会正负 抵消，即 ∑∑b·b,=0 (2-4) 这样我们就可以得到 〈R:）=b2 (2-5) 式(2-5)中的(.)表示对许多条高分子链系综平均的结果，因而这一结果被称为高 分子链的均方未端距(mean-square end-to-end distance)。 如果把自由连接链的构象比拟成布朗运动无规行走的轨迹，链长对应于所走 的步数，即行走时间的长短，我们就可以看出，以上结果与爱因斯坦早在1905年对 布朗运动计算的经典结果是一致的，即布朗运动粒子的均方位移与时间成正比 (Einstein A.Investigations on the theory of the Brownian movement.Ann Phys (Leipzig),1905,17:549-560)。这一相似性说明了高分子的无规链构象实际上 是所有链单元在做随机布朗运动的松弛结果。 第二种也许是更常用的线团尺寸表征量是所谓的均方回转半径(mean-square radius of gyration)。这一尺寸比均方末端距更具可操作性。这是因为其被定义为 所有链单元相对于高分子线团质量中心的均方位移之和，并且此结果可以由光散 射实验直接测量得到。对n+1个质量为的链单元相对于整个高分子链质量中 心的矢量”平方加和，对质量取平均，就可以定义均方回转半径。 mri (R)==0 (2-6) =0 可以通过简单的推导证明，当高分子链足够长的时候，有 (R〉=(R,) (2-7) 2.2.2自由旋转链 高分子材料的主链实际上往往是以碳一碳共价键连接而成的。碳原子的共价

૓૓ຯ᳉ᄦ䋠์็⮱倅ܳၽ䨫ःᎠ౴㐀᳉ಎ䮼ᱧःा⮱᱘〜䌊ⴏ䛼ᄳౕ㐀᳉͚Ⱕ ο២⊵ᢶ૕఍ₑಎ᜾Й䰭㺮ᥳ㙞ᄩ㜡㐀᳉២⊵⮱ⴏ䛼᫦ाԎᖜಎ⩕̭͗ᴴ䛼ಎࢠ᱘ 〜䌊⮱Ꭰ᫦ಎऍߍ䊤Გ㶕ᒮ倅ܳၽ㏬ఏ⮱➦ᒮᅧᄥ૕ ਣಕ ಉ ૺ ੄ ਾಉಔ ਵਾ૖ૺ ੄ ਿಉಔ ਵਿ ಉ੄ਵಕ ౵ಕૺૺ ਿಢਾ ਵਾ૖ਵਿ ಉಕ႗ಕಊ ૓૓⩞λ͑͗ⴏ䛼⮱◦⼜㐀᳉ͨ㺮ः۠λᒩₑ⮱๦㻿ກਾਿಎ ਵਾ૖ਵਿ ಉਵಕ૖ੋਗ਼੟ກਾਿ ಉಕ႗ಖಊ 㔹㜗⩞䔋ᣒ䨫̷⮱Шᘼ̺͑͗ह䩛ⴏ䛼⮱๦㻿जВౕಓݝಕວ͸䬡౴࠭ܳጰಎᄩ㜡 ڣ҆ᑓթౕಏಔহಔ͸䬡౴࠭ܳጰಎ䋠์็䔆ᵤ⠙⿸⮱◦⼜ߍহ⮱㐀᳉ᅞчₐ䉌 ២⊵ಎࢠ ૺૺ ਿಢਾ ਵਾ૖ਵਿ ಉಓ ಉಕ႗ಗಊ 䔆ᵤ᜾ЙᅞजВᓄݝ ૨ਣಕ ੏Ⴐ੔Ⴐ૩ಉ੄ਵಕ ಉಕ႗ಘಊ ᐼಉಕႱಘಊ͚⮱૨ૡ૩㶕⹧ᄦ䃥็᲎倅ܳၽ䨫㈨㐩Ꭰ౴⮱㐀᳉ಎ఍㔹䔆̭㐀᳉㷘⼝ͧ倅 ܳၽ䨫⮱౴᫦᱘〜䌊౱੃ਹ਴੄႗੊ੇੌ਴੉ਹਹ੄ਸ႗ੋ੅႗ਹ੄ਸਸਾ੊ੋ਴੄ਸ਼ਹ౲૕ ຯ᳉ិ㜗⩞䔋ᣒ䨫⮱Ჱ䆎℁᠌᜽ጰ᱄䓽ߕᬍ㻱㵹䊝⮱䒕䔦ಎ䨫䪬ᄦᏁλ᝭䊝 ⮱ₒ᪝ಎࢠ㵹䊝ᬣ䬡⮱䪬ⴚಎ᜾ЙᅞजВⰸܧಎВ̷㐀᳉̻❞఍᫜ಓᬖౕಔಝಓಘᎡᄦ ጰ᱄䓽ߕ䃎ツ⮱㏼ڥ㐀᳉᭜̭㜡⮱ಎࢠጰ᱄䓽ߕㆿၽ⮱౴᫦Ѻ⼨̻ᬣ䬡᜽ₐ℁ ಉ਩੓ਖ਼੟੠੎੓ਖ਼ਥႰਮਖ਼੢੎੟੠੓ੑ੉੠੓ਗ਼ਖ਼੟ਗ਼ਖ਼੠੒੎੠੒੎ਗ਼ਫ਼੥ਗ਼੏੠੒੎ਦਫ਼ਗ਼੣ਖ਼੓੉ਖ਼੘ਗ਼੢੎੘੎ਖ਼੠಑ਥਖ਼ਖ਼ਵ੒੥੟ ಉ਱੎੓ਜ਼੦੓ੑಊಎಔಝಓಘಎಔಚಞಘಗಝႱಘಙಓಊ૕䔆̭Ⱕѩᕔ䄡ᬻγ倅ܳၽ⮱ᬍ㻱䨫Ჱ䆎჋䭲̷ ᭜᝭ᰶ䨫ࢂٰౕև䮼ᱧጰ᱄䓽ߕᲫ⮱ᑈ㐀᳉૕ すι⻺Ό䃥᭜ᰡ፥⩕⮱㏬ఏᅧᄥ㶕ᒮ䛼᭜᝭䅀⮱౴᫦ఋ䒙ࡷᒱ౱੃ਹ਴੄႗੊ੇੌ਴੉ਹ ੉਴ਸਾੌ੊੅਺਼੐੉਴ੋਾ੅੄౲૕䔆̭ᅧᄥ℁౴᫦᱘〜䌊ᰡڤज᧺҉ᕔ૕䔆᭜఍ͧڣ㷘ჇͶͧ ᝭ᰶ䨫ࢂٰⰥᄦλ倅ܳၽ㏬ఏ䉕䛼͚ᓰ⮱౴᫦Ѻ⼨͸হಎᎣ́ₑ㐀᳉जВ⩞وٴ᪐ ᄱ჋侹Ⱑᣒ≸䛼ᓄݝ૕ᄦ੄಍ಔ͗䉕䛼ͧ੃ ⮱䨫ࢂٰⰥᄦλ᪡͗倅ܳၽ䨫䉕䛼͚ ᓰ⮱ⴏ䛼੉Ꭰ᫦ߍহಎᄦ䉕䛼ःᎠ౴ಎᅞजВჇͶ౴᫦ఋ䒙ࡷᒱ૕ ૨ਣಕ ੑ૩ଈ ૺ ੄ ਾಉಓ ੃ਾ੉ಕ ਾ ૺ ੄ ਾಉಓ ੃ਾ ಉಕ႗ಙಊ जВ䕇䓴キࢂ⮱ᣕᄩ䃮ᬻಎᒀ倅ܳၽ䨫䋠์䪬⮱ᬣՆಎᰶ ૨ਣಕ ੑ૩ಉ ಔ ಙ૨ਣಕ ੏Ⴐ੔Ⴐ૩ ಉಕ႗ಚಊ ౽႖౽႖౽ 㜗⩞᫸䒙䨫 倅ܳၽᱽ᫆⮱ͨ䨫჋䭲̷ᒭᒭ᭜Вⷠ૞ⷠڞФ䩛䔋ᣒ㔹᜽⮱૕ⷠ࣌ၽ⮱ڞФ すಕ」 䨫ࡃ႓㐀Ჱ⮱㶕ᒮ ૖ಔಖ૖

·14. 高分子物理导论 键连接在化合物中采用四面体的sp3杂化轨道，键角接近于109°28'。也就是说， 实际高分子链单元之间的连接要考虑固定键角的限制。但是，我们仍可以看到，沿 着主链下一个键绕着前一个键在保持键角不变的情况下可发生内旋转。假定内旋 转没有遇到任何阻碍，这就是自由旋转链(free-rotating chain)模型。如图2-l所 示，下一个键矢量与前一个键矢量之间的夹角被定义为日，对于碳原子构成的主 链，0=180°一10928'。理论上可以推导出包含固定键角假设的自由旋转链的均方 末端距，其对自由连接链的均方末端距有一个固定键角贡献的修正。 =法 (2-8) 2.2.3受阻旋转链 实际的高分子主链在发生内旋转时，侧基之间会发生相互作用，给内旋转带来 阻碍，这就有必要再进一步考虑受阻旋转链(hindered-rotating chain)模型。如 图2-1所示，沿着高分子主链的某一键以固定的键角围绕着前一个键发生内旋转， 这样其末端就构成一个旋转面。如果我们把其前面两个主链键构成的面在该旋转 面上的交线作为参考方向，就可以把所考察的主链键在其旋转面上的投影与参考 方向所成的角度定义为内旋转角中，如图2-1所示。例如，当乙烷(CH。一CH)分 子两个碳原子上的氢原子基团处在内旋转重叠位时，彼此之间的距离为2.26A,小 于两个氢原子的范德瓦耳斯半径之和2.40A,因此，强烈的体积排斥相互作用使内 旋转势能升高，对构象的稳定不利。如果这两个碳上的氢原子彼此以内旋转角 60°相互错开，就可以有效地降低内旋转势能E(),如图2-2所示。 图2-1高分子链的内旋转角中示意图 如果乙烷的两个碳原子上各有一个氢原子分别被一个很大的基团R所取代， 例如聚乙烯主链上某个C一C键一侧的剩余高分子链，则两侧高分子链之间的相 互作用将大大提升重叠位内旋转势能的变化幅度，并拉开其与旁式位的差距。如

䩛䔋ᣒౕࡃव➖͚䛴⩕ఈ䲏Ҁ⮱੟ਜ਼ಖ ᱯࡃ䒕䖀ಎ䩛㻿ᣒ䓾λಔಓಝଗಕಛଙ૕Όᅞ᭜䄡ಎ ჋䭲倅ܳၽ䨫ࢂ͸ٰ䬡⮱䔋ᣒ㺮㔰㭾ధჇ䩛㻿⮱䭽ݣ૕ѳ᭜ಎ᜾ЙϺजВⰸݝಎ⇬ Ɑͨ䨫̸̭͗䩛㐂Ɑݺ̭͗䩛ౕԊᠮ䩛㻿̺अ⮱ᗲ̸ۢजࣾ⩌ڲ᫸䒙૕մჇڲ᫸ 䒙⇎ᰶ䕴ݝШ҂䭨ⶺಎ䔆ᅞ᭜㜗⩞᫸䒙䨫౱਺੉ਹਹ႗੉੅ੋ਴ੋਾ੄਼ਸ਼਽਴ਾ੄౲὎ಸ૕ຯఫಕႱಔ᝭ ⹧ಎ̸̭͗䩛ⴏ䛼̻ݺ̭͗䩛ⴏ䛼͸䬡⮱๦㻿㷘ჇͶͧງಎᄦλⷠ࣌ၽᲱ᜽⮱ͨ 䨫ಎງಡಔಛಓଗಏಔಓಝଗಕಛଙ૕⤳䃧̷जВᣕᄩ࠲ܧक़ధჇ䩛㻿մ䃫⮱㜗⩞᫸䒙䨫⮱౴᫦ ᱘〜䌊ಎڣᄦ㜗⩞䔋ᣒ䨫⮱౴᫦᱘〜䌊ᰶ̭͗ధჇ䩛㻿䉎⡛⮱ԛₐ૕ ૨ਣಕ ੏Ⴐਫ਼Ⴐ૩ಉ੄ਵಕ૖ಔ౵ੋਗ਼੟ງ ಔ౷ੋਗ਼੟ງ ಉಕ႗ಛಊ ౽႖౽႖౾ ऄ䭨᫸䒙䨫 ჋䭲⮱倅ܳၽͨ䨫ౕࣾ⩌ڲ᫸䒙ᬣಎӔധ͸䬡чࣾ⩌Ⱕο҉⩕ಎ㐆ڲ᫸䒙ፓᲒ 䭨ⶺಎ䔆ᅞᰶᓲ㺮ں䔈̭ₒ㔰㭾 ऄ䭨᫸䒙䨫 ౱਽ਾ੄ਸਹ੉ਹਸ႗੉੅ੋ਴ੋਾ੄਼ਸ਼਽਴ਾ੄౲὎ ಸ૕ຯ ఫಕႱಔ᝭⹧ಎ⇬Ɑ倅ܳၽͨ䨫⮱᳽̭䩛ВధჇ⮱䩛㻿డ㐂Ɑݺ̭͗䩛ࣾ⩌ڲ᫸䒙ಎ 䔆ᵤڣ᱘〜ᅞᲱ᜽̭͗᫸䒙䲏૕ຯ᳉᜾Йិݺڣ䲏͑͗ͨ䨫䩛Ჱ᜽⮱䲏ౕ䄒᫸䒙 䲏̷⮱ϑ㏬҉࣯ͧ㔰᫦ाಎᅞजВិ᝭㔰ᄌ⮱ͨ䨫䩛ౕڣ᫸䒙䲏̷⮱ែᒞ̻࣯㔰 ᫦ा᝭᜽⮱㻿ᏓჇͶͧڲ᫸䒙㻿๺ಎຯఫಕႱಔ᝭⹧૕ҸຯಎᒀΆ☤ಉਧਭಖ૞ਧਭಖಊܳ ၽ͑͗ⷠ࣌ၽ̷⮱⅏࣌ၽധఏัౕڲ᫸䒙䛺ऍѺᬣಎᒩₑ͸䬡⮱䌊⻨ͧಕႰಕಙሼಎᄼ λ͑͗⅏࣌ၽ⮱㠰ᓤ⨓㕠᫜ࡷᒱ͸হಕႰಗಓሼಎ఍ₑಎᑧ◵⮱Ҁ⼜ᢿ᫒Ⱕο҉⩕Ҭڲ ᫸䒙߬㘪ࡴ倅ಎᄦᲱ䆎⮱⽠Ⴧ̺ݖ૕ຯ᳉䔆̷͑͗ⷠ⮱⅏࣌ၽᒩₑВڲ᫸䒙㻿 ಙಓଗⰥο䩆ᐭಎᅞजВᰶ᩵ౝ䭺ѻڲ᫸䒙߬㘪ਔಉ๺ಊಎຯఫಕႱಕ᝭⹧૕ ఫಕႱಔ૓倅ܳၽ䨫⮱ڲ᫸䒙㻿๺⹧ᘼఫ ຯ᳉Ά☤⮱͑͗ⷠ࣌ၽ̷ऱᰶ̭͗⅏࣌ၽܳݘ㷘̭͗ᒵ๔⮱ധఏ ਸ ᝭ःАಎ Ҹຯ㖇Ά☜ͨ䨫̷᳽͗ ਧ૞ਧ䩛̭Ӕ⮱ޖ҆倅ܳၽ䨫ಎ݆͑Ӕ倅ܳၽ䨫͸䬡⮱Ⱕ ο҉⩕ᄳ๔๔᣽ࡴ䛺ऍѺڲ᫸䒙߬㘪⮱अࡃ፲ᏓಎᎣ៶ᐭڣ᫮̻ᐼѺ⮱ጛ䌊૕ຯ ૖ಔಗ૖ 倅ܳၽ➖⤳ᄩ䃧

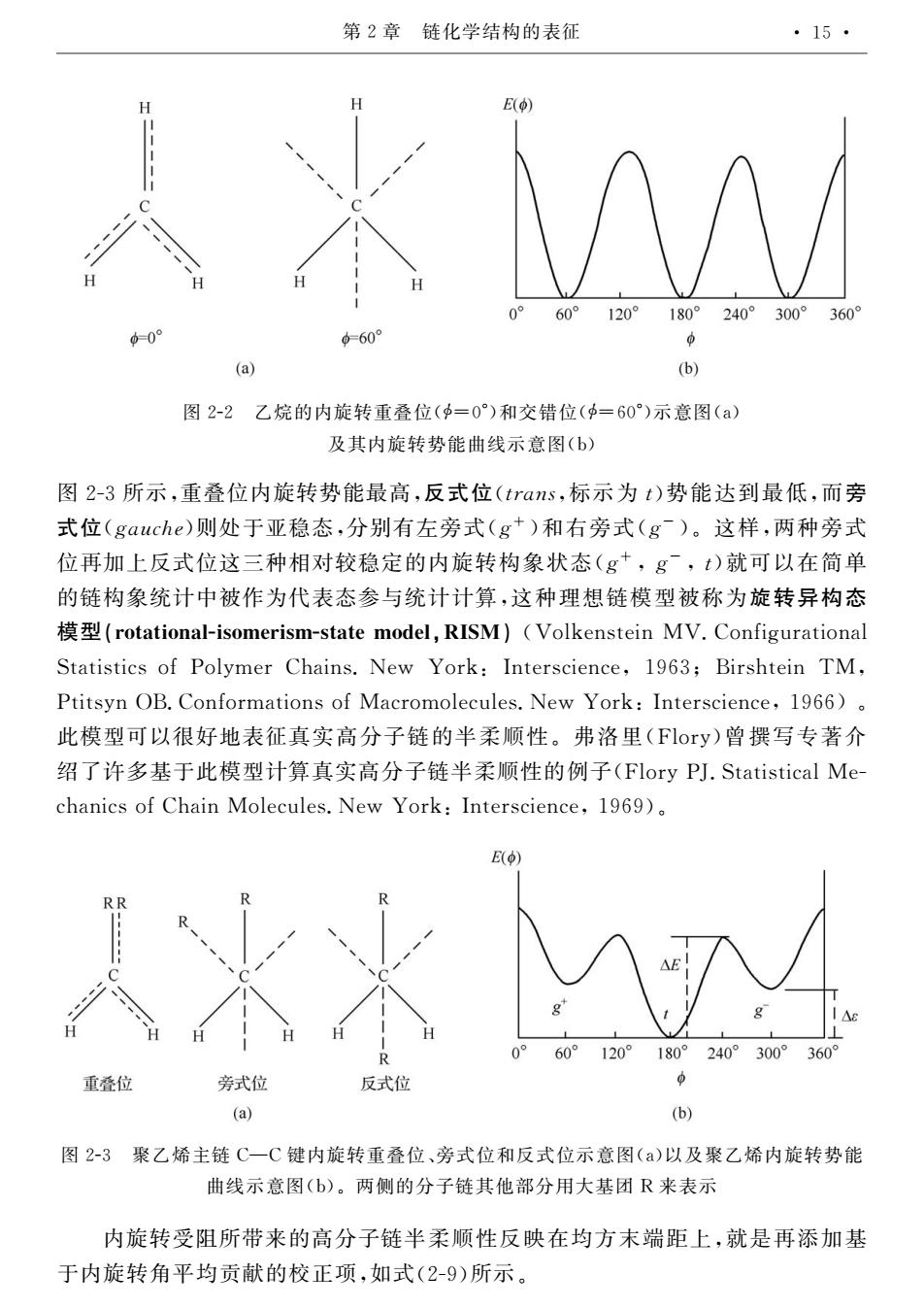
第2章链化学结构的表征 ·15· 60°120°180°240°300 (b) 图2-2乙烷的内旋转重叠位（中=0°）和交错位（中=60°）示意图() 及其内旋转势能曲线示意图(b) 图2-3所示，重叠位内旋转势能最高，反式位(trans,标示为t)势能达到最低，而旁 式位(gauche)则处于亚稳态，分别有左旁式(g+)和右旁式(g)。这样，两种旁式 位再加上反式位这三种相对较稳定的内旋转构象状态(g+,gˉ，)就可以在简单 的链构象统计中被作为代表态参与统计计算，这种理想链模型被称为旋转异构态 (rotational-isomerism-state model,RISM)(Volkenstein MV.Configurational Statistics of Polymer Chains.New York:Interscience,1963;Birshtein TM, Ptitsyn OB.Conformations of Macromolecules.New York:Interscience,1966) 此模型可以很好地表征真实高分子链的半柔顺性。弗洛里(Flory)曾撰写专著介 绍了许多基于此模型计算真实高分子链半柔顺性的例子(Flory PJ.Statistical Me chanics of Chain Molecules.New York:Interscience,1969). 叠位 旁式位 反式 (a) 6 图2-3聚乙烯主链C一C键内旋转重叠位、旁式位和反式位示意图()以及聚乙烯内旋转势能 曲线示意图(b)。两侧的分子链其他部分用大基团R来表示 内旋转受阻所带来的高分子链半柔顺性反映在均方末端距上，就是再添加基 于内旋转角平均贡献的校正项，如式(2-9)所示

ఫಕႱಕ૓Ά☤⮱ڲ᫸䒙䛺ऍѺಉ๺ಡಓଗಊহϑ䩆Ѻಉ๺ಡಙಓଗಊ⹧ᘼఫಉ੉ಊ ڲڣࣷ᫸䒙߬㘪ᰟ㏬⹧ᘼఫಉ੊ಊ ఫಕႱಖ᝭⹧ಎ䛺ऍѺڲ᫸䒙߬㘪ᰭ倅ಎࣺᐼѺಉੋ੉਴੄੊ಎᴴ⹧ͧੋಊ߬㘪䓫ݝᰭѻಎ㔹᫮ ᐼѺಉ਼਴ੌਸ਼਽ਹಊ݆ัλχ⽠ᔮಎܳݘᰶጓ᫮ᐼಉ਼಍ ಊহठ᫮ᐼಉ਼ಏ ಊ૕䔆ᵤಎ͑⻺᫮ᐼ Ѻߍں̷ࣺᐼѺ䔆̶⻺Ⱕᄦ䒰⽠Ⴧ⮱ڲ᫸䒙Ჱ䆎⟣ᔮಉ਼಍ ಎ਼ಏ ಎੋಊᅞजВౕキࢂ ⮱䨫Ჱ䆎㐌䃎͚㷘҉ͧА㶕ᔮ࣯̻㐌䃎䃎ツಎ䔆⻺⤳ᘠ䨫὎ಸ㷘⼝ͧ᫸䒙ᐯᲱᔮ ὎ಸ౱੉੅ੋ਴ੋਾ੅੄਴ੁ႗ਾ੊੅੃ਹ੉ਾ੊੃႗੊ੋ਴ੋਹ੃੅ਸਹੁ౶ਣਙਤਝ౲ಉ਼ਗ਼੖੕੎ਖ਼੟੠੎੓ਖ਼ ਲ਼಑ਧਗ਼ਖ਼੏੓ੑ੡ਫ਼੉੠੓ਗ਼ਖ਼੉੖ ਹ੠੉੠੓੟੠੓ੋ੟ਗ਼੏ਵਗ਼੖੥੘੎ਫ਼ ਧ੒੉੓ਖ਼੟಑ਲ਼੎੣ ੀਗ਼ਫ਼੕ಞਮਖ਼੠੎ਫ਼੟ੋ੓੎ਖ਼ੋ੎ಎಔಝಙಖಟਦ੓ਫ਼੟੒੠੎੓ਖ਼ ਺ਲಎ ਵ੠੓੠੟੥ਖ਼਴ਦ಑ਧਗ਼ਖ਼੏ਗ਼ਫ਼੘੉੠੓ਗ਼ਖ਼੟ਗ਼੏ਲ੉ੋਫ਼ਗ਼੘ਗ਼੖੎ੋ੡੖੎੟಑ਲ਼੎੣ ੀਗ਼ਫ਼੕ಞਮਖ਼੠੎ਫ਼੟ੋ੓੎ਖ਼ੋ੎ಎಔಝಙಙಊ૕ ₑ὎ಸजВᒵສౝ㶕ᒮⱌ჋倅ܳၽ䨫⮱ࡷᴁ䶧ᕔ૕ᑄ≈䛹ಉਪ੖ਗ਼ਫ਼੥ಊᰫ᧝ۆ̀㦄ϸ ㏺γ䃥็ധλₑ὎ಸ䃎ツⱌ჋倅ܳၽ䨫ࡷᴁ䶧ᕔ⮱Ҹၽಉਪ੖ਗ਼ਫ਼੥ਵਯ಑ਹ੠੉੠੓੟੠੓ੋ੉੖ਲ੎Ⴑ ੋ੒੉ਖ਼੓ੋ੟ਗ਼੏ਧ੒੉੓ਖ਼ਲਗ਼੖੎ੋ੡੖੎੟಑ਲ਼੎੣ ੀਗ਼ਫ਼੕ಞਮਖ਼੠੎ਫ਼੟ੋ੓੎ਖ਼ੋ੎ಎಔಝಙಝಊ૕ ఫಕႱಖ૓㖇Ά☜ͨ䨫 ਧ૞ਧ䩛ڲ᫸䒙䛺ऍѺ૔᫮ᐼѺহࣺᐼѺ⹧ᘼఫಉ੉ಊВࣷ㖇Ά☜ڲ᫸䒙߬㘪 ᰟ㏬⹧ᘼఫಉ੊ಊ૕͑Ӕ⮱ܳၽ䨫ڣЃ䘕ܳ⩕๔ധఏ ਸᲒ㶕⹧ ڲ᫸䒙ऄ䭨᝭ፓᲒ⮱倅ܳၽ䨫ࡷᴁ䶧ᕔࣺ᫦౴ౕ᭍᱘〜䌊̷ಎᅞ᭜ں⌨ߍധ λڲ᫸䒙㻿Ꭰ౴䉎⡛⮱ᵎₐ䶦ಎຯᐼಉಕႱಝಊ᝭⹧૕ すಕ」 䨫ࡃ႓㐀Ჱ⮱㶕ᒮ ૖ಔಘ૖