中国科学技术大学：《数字逻辑电路》课程教学资源（课件讲稿）第二章 逻辑代数基础

§2.3逻辑代数的基本公式和常用公式 2.3.1基本公式 。根据与、或、非的定义， 得表2.3.1的布尔恒等式 序号 公式 序号 公 式 10 1=0;0=1 1 0A=0 11 1+A=1 2 1A=A 12 0+A=A 3 AA-A 13 A+A=A 4 A4-0 14 A+A'=1 5 AB=BA 15 A+B=B+A 6 A(B C)=(AB)C 16 A+(B+C)=(A+B)+C 7 A(B+C)=AB+AC 17 A+BC=(A+B)(A+C) 8 (AB)=A+B' 18 (A+B)=A'B' 9 (A)'=A 2017-8-4 第二章逻辑代数基础 §2.3 逻辑代数的基本公式和常用公式 公式(17)的证明 (真值表法)：A+BC=(A+B)(A+C ABC BC A+BC 4+B A+C (A+B)(A+C) 000 0 0 0 0 0 001 0 0 0 1 0 010 0 0 1 0 0 011 1 1 1 1 1 100 0 1 1 1 1 101 0 1 1 1 1 110 0 1 1 1 1 111 1 1 1 1 1 公式(8) 和公式(18) 的证明：(AB)=A+B,(A+B)=B A B (AB)' A'+B' (A+B)' A'B' 0 0 1 1 1 1 0 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 0 0 2017-8-4 第二章逻辑代数基础 12

2017-8-4 第二章 逻辑代数基础 11 • 根据与、或、非的定义，得表2.3.1的布尔恒等式 9 (A')' = A 8 (A B)'= A'+ B' 18 (A+ B)'= A'B' 7 A (B +C) = A B + A C 17 A + B C = (A +B)(A +C) 6 A (B C) = (A B) C 16 A + (B +C) = (A + B) + C 5 A B = B A 15 A +B = B + A 4 A A'= 0 14 A + A' = 1 3 A A = A 13 A + A = A 2 1·A = A 12 0 + A = A 1 0·A = 0 11 1 + A= 1 10 1'= 0; 0'= 1 序号 公 式 序号 公 式 §2.3 逻辑代数的基本公式和常用公式 2.3.1 基本公式 2017-8-4 第二章 逻辑代数基础 12 公式（17）的证明（真值表法）： 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 ABC BC A+BC A+B A+C (A+B)(A+C) §2.3 逻辑代数的基本公式和常用公式 A + BC = (A +B)(A +C) 公式（8）和公式（18）的证明：(AB)'= A'+B',(A+ B)'= A'B' 1 1 0 0 0 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 1 A B (A B)' A'+ B' (A+ B)' A'B

§2.3逻辑代数的基本公式和常用公式 2.3.2若干常用公式 序号 公 式 21 A+AB=A 22 A+A'B=A+B 23 AB+AB'=A 24 A(A+B)=A AB+A'C+BC=AB+AC 25 AB+A'C+BCD=AB+A'C 26 A(AB)=AB';A(AB)=A' 2017-8-4 第二章逻辑代数基础 13 §2.4逻辑代数的基本定理 2.4.1代入定理 在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式取 代式中所有A的位置，则等式仍然成立。 例1：基本公式（17) A+BC=(A+B)(A+C用C.D取代C A+B(CD)=(A+B)(A+CD) =(A+B)(A+C)(A+D) 例2：基本公式（18) (A+B)'=A'.B' 用(B+C)取代B (A+(B+C))'=A'.(B+C)=4'.B'.C" 2017-8-4 第二章逻辑代数基础 14

2017-8-4 第二章 逻辑代数基础 13 26 A (AB)'= AB' ; A'(AB)'= A' A B + A'C + B C = A B + A'C A B + A'C + B CD = A B + A'C 25 24 A ( A + B) = A 23 A B + A B' = A 22 A +A'B = A + B 21 A + A B = A 序 号 公 式 §2.3 逻辑代数的基本公式和常用公式 2.3.2 若干常用公式 2017-8-4 第二章 逻辑代数基础 14 §2.4 逻辑代数的基本定理 2.4.1 代入定理 在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式取 代式中所有A的位置，则等式仍然成立。 例2：基本公式（18） (A+ B)′ = A′⋅ B′ 用(B +C)取代B ⇒ (A+ (B +C))′ = A′⋅(B +C)′ = A′⋅ B′⋅C′ 例1：基本公式（17） = (A+B)(A+C)(A+D) A+BC= (A+B)(A+C) A+B(CD) = (A+B)(A+CD) 用C ⋅ D取代C

§2.4逻辑代数的基本定理 2.4.2反演定理 对于任意一个逻辑式Y,若将其中所有的“换成“+”，“+”换 成“”，0换成1,1换成0，原变量换成反变量，反变量换成原 变量，则得到的结果就是Y'。 注意： (1)需遵守“先括号、然后乘、最后加”的运算优先次序。 (2)不属于单个变量上的反号应保留不变。 例1：Y=A(B+C)+CD Y'=(A'+B'C)(C'+D) =A'C+B'C+A'D'+B'C'D'=A'C+B'C'+AD' 例2：Y=(AB'+Cy+DY+C Y'=((A'+B)C)D)'C 2017-8-4 第二章逻辑代数基础 §2.4逻辑代数的基本定理 2.4.3对偶定理 若两逻辑式相等，则它们的对偶式也相等。 对偶式：对于任意一个逻辑式Y,若将其中所有的“”换成 “+”,“+”换成”，0换成1,1换成0，则得到一个新的逻辑式 D,这个D就称为Y的对偶式。 例1：Y=AB+(C+D)Y Y=(A+B)(CD) 例2：证明表2.3.1中的式(17)A+BC=(A+B)A+C 证明：写出等式两边的对偶式 A(B+C)=AB+AC 2017-8-4 第二章逻辑代数基础 16

2017-8-4 第二章 逻辑代数基础 15 §2.4 逻辑代数的基本定理 2.4.2 反演定理 对于任意一个逻辑式Y，若将其中所有的“·”换成“+”，“+”换 成“·” ，0换成1，1换成0，原变量换成反变量，反变量换成原 变量，则得到的结果就是Y ′ 。 注意： （1）需遵守“先括号、然后乘、最后加”的运算优先次序。 （2）不属于单个变量上的反号应保留不变。 例1：Y = A(B +C) +CD A C B C A D B C D A C B C A D Y' A B C C D = ′ ′ + ′ ′ + ′ ′ + ′ ′ ′ = ′ ′ + ′ ′ + ′ ′ = ′ + ′ ′ ′ + ′ ( )( ) 例2：Y = ((AB' +C)' + D)' +C Y' = (((A' + B)C')'D')'C' 2017-8-4 第二章 逻辑代数基础 16 §2.4 逻辑代数的基本定理 2.4.3 对偶定理 对偶式：对于任意一个逻辑式Y，若将其中所有的“·”换成 “+”，“+”换成“·” ，0换成1，1换成0，则得到一个新的逻辑式 YD ，这个YD就称为Y的对偶式。 例1： 例2：证明表2.3.1中的式（17）A+BC= (A+B)(A+C) 若两逻辑式相等，则它们的对偶式也相等。 Y = AB + (C + D)' Y A B CD ' D = ( + )( ) 证明：写出等式两边的对偶式 A(B+C)=AB+AC

§2.5逻辑函数及其描述方法 2.5.1逻辑函数 描述输入逻辑变量与输出逻辑变量之间因果关系的函数， 写作：Y=FA,B,C,) 注：在二值逻辑中，输入输出都只有两种取值0/1。 例：举重裁判电路 若以1表示开关闭合，0表示开 关断开；以1表示灯亮，0表示 灯暗；则指示灯Y是开关A、 B、C的二值逻辑函数，即 Y=F(A,B,C) 2017-8-4 第二章逻辑代数基础 §2.5逻辑函数及其描述方法 2.5.2逻辑函数的描述方法 一、常用的逻辑函数的描述方法 逻辑真值表、逻辑函数式、逻辑图、波形图、卡诺图和硬件 描述语言。 逻辑真值表：输入逻辑变量所有可能的取值组合与对应的输 出逻辑函数值构成的表格。 逻辑函数式：用与、或、非等运算组合起来，表示逻辑函数 的输出与输入逻辑变量之间关系的逻辑代数式。 逻辑图：用与、或、非等逻辑符号表示输出与输入之间逻辑 关系的图形。 波形图：将输入变量所有可能的取值组合与对应的输出按时 间顺序依次排列起来画成的时间波形。 2017-8-4 第二章逻辑代数基础 18

2017-8-4 第二章 逻辑代数基础 17 §2.5 逻辑函数及其描述方法 2.5.1 逻辑函数 Y=F(A,B,C,······) 描述输入逻辑变量与输出逻辑变量之间因果关系的函数， 写作： 注：在二值逻辑中，输入/输出都只有两种取值0/1。 例：举重裁判电路 若以1表示开关闭合，0表示开 关断开；以1表示灯亮，0表示 灯暗；则指示灯 Y 是开关A、 B、C的二值逻辑函数，即 Y=F(A,B,C) 2017-8-4 第二章 逻辑代数基础 18 2.5.2 逻辑函数的描述方法 逻辑真值表、逻辑函数式、逻辑图、波形图、卡诺图和硬件 描述语言。 一、常用的逻辑函数的描述方法 逻辑真值表：输入逻辑变量所有可能的取值组合与对应的输 出逻辑函数值构成的表格。 逻辑函数式：用与、或、非等运算组合起来，表示逻辑函数 的输出与输入逻辑变量之间关系的逻辑代数式。 逻辑图：用与、或、非等逻辑符号表示输出与输入之间逻辑 关系的图形。 波形图：将输入变量所有可能的取值组合与对应的输出按时 间顺序依次排列起来画成的时间波形。 §2.5 逻辑函数及其描述方法

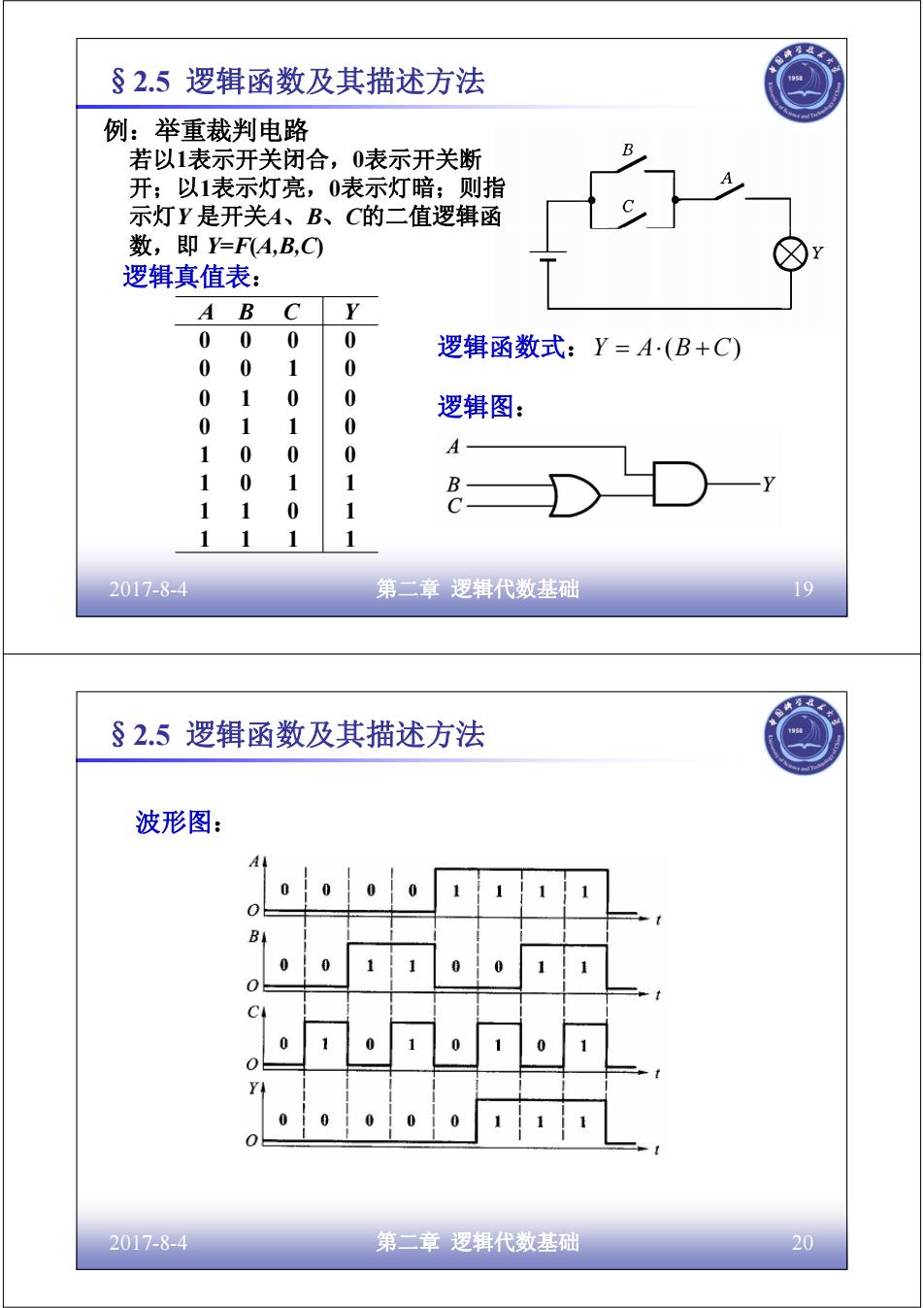
§2.5逻辑函数及其描述方法 例：举重裁判电路 若以1表示开关闭合，0表示开关断 B 开；以1表示灯亮，0表示灯暗；则指 示灯Y是开关A、B、C的二值逻辑函 数，即Y=FA,B,C 逻辑真值表： A B C Y 0 0 0 0 逻辑函数式：Y=A(B+C) 00 1 0 01 0 0 逻辑图： 0 1 1 0 1 0 0 0 A 1 0 1 1 B 1 1 0 1 1 2017-8-4 第二章逻辑代数基础 19 §2.5逻辑函数及其描述方法 波形图： A 00 1 B C 0 2017-8-4 第二章逻辑代数基础 20

2017-8-4 第二章 逻辑代数基础 19 例：举重裁判电路 若以1表示开关闭合，0表示开关断 开；以1表示灯亮，0表示灯暗；则指 示灯Y 是开关A、B、C的二值逻辑函 数，即 Y=F(A,B,C) 1 1 1 1 1 1 0 1 1 0 1 1 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 A B C Y 逻辑真值表： 逻辑函数式：Y = A⋅(B +C) 逻辑图： §2.5 逻辑函数及其描述方法 2017-8-4 第二章 逻辑代数基础 20 波形图： §2.5 逻辑函数及其描述方法