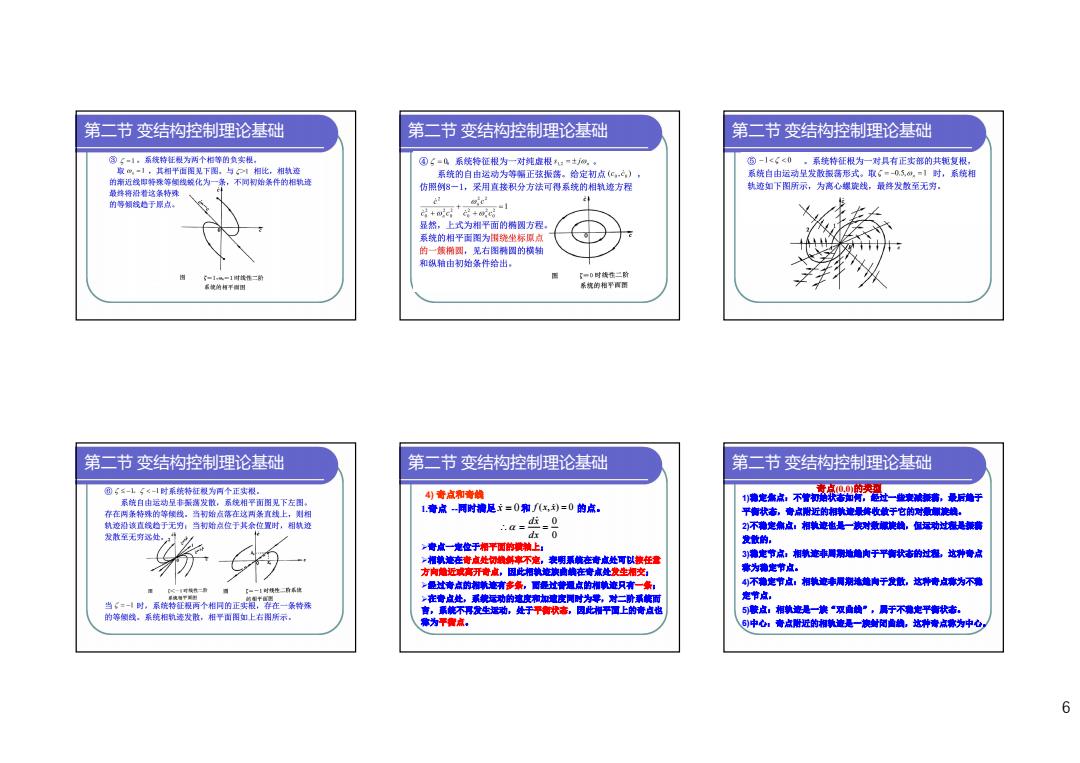
第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 ③(一1。系统特任根为两个相等的负实根。 ④(=心系统特征根为一对纯虚根=士m,。 的-1<(<0。系统特征根为一对具有正实部的共瓶复根, 家m,1,其相平面图见下图。与⊙1相比,相轨迹 系统的自由运动为等需正弦振篱。给定初点(c,心,), 系统自由运动呈发放数稿形式。取6■0,5,做,-1时,系统相 的南近线即特骤等领线锐化为一条,不司脚始条件的相轨迹 最蜂将沿着这条特辣 仿照例8一1,采用直接积分方法可得系统的相轨迹方程 缺迹如下图所示,为离心螺旋线,最终发敏至无穷。 的等领线趋于原点, 4 ++花 显然,上式为相平面的椭圆方程 系统的相平面图为围绕坐标原点 的一核椭圆,见右图裤圆的横轴 和纵箱由初始条件给出, G-1k-1时线准二静 【=D时线在二阶 系统的相干国 系的相平 第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 团5名-15《-1时系统特缸根为两个正实根。 )奇点和青情 系饶白由运动星非最落发散,系统相平面图见下左图。 电k点不常亮条醉止-精。电后于 存在两条特殊的等便线。当初始点落在这两条直线上,则烟 1音点两时满足i=0和(x,动=0的点。 平衡状志,青点附近的相轨边绿共收敏于它的对量旋线。 轨迹沿该直线趋于无穷:当初始点位于其余位置时,相轨迹 2)不物定南点:相铁迹也是一对数块地,但记动过程是振满 发散至无穷远处。: dx 0 发数的。 青点一电位于悟平面的黄输上: 一帽轨達在奇点处心懒事不毫,妻明弧黄在责点处可以整任意 3到海定节点:相轨迹非周测地地肉于平青状本的过程这种青点 方向抛近成高开诗点,因此相教地族曲典在奇减处发生相交 常为微定节点。 【=一1时W性一育系德 产是过青点的相缘迹请多条,面是址普通点的相慎迹只有一条: 4不物定节点:相换边本调期地黄★于发散,达升青点事常为不薄 当一时,系污个相同的正尖容在一条特 ,在毒点此,系款运功的速度和加知速皮同时为零,对二阶票黄而 定节点, 5)联点:相轨边是一换“双曲黄”,周于不定平青状者。 的等侧线。系统相物迹发散,相平面图如上右图所示, 青,系铁不厚发生运动。处于早衡状格,因此湘平国上的青点出 常为平智点。 6)中心1青点附近的相轨造是一澳封闭曲线,这种青点淋为中心, 6
6 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础 4) 奇点和奇线 1.奇点 --同时满足 和 的点。 x 0 f x x ( , ) 0 奇点一定位于相平面的横轴上; 相轨迹在奇点处切线斜率不定,表明系统在奇点处可以按任意 方向趋近或离开奇点,因此相轨迹族曲线在奇点处发生相交; 经过奇点的相轨迹有多条,而经过普通点的相轨迹只有一条; 在奇点处,系统运动的速度和加速度同时为零,对二阶系统而 言,系统不再发生运动,处于平衡状态,因此相平面上的奇点也 称为平衡点。 0 0 dx dx 第二节 变结构控制理论基础 奇点(0,0)的类型 1)稳定焦点:不管初始状态如何,经过一些衰减振荡,最后趋于 平衡状态,奇点附近的相轨迹最终收敛于它的对数螺旋线。 2)不稳定焦点:相轨迹也是一族对数螺旋线,但运动过程是振荡 发散的, 3)稳定节点:相轨迹非周期地趋向于平衡状态的过程,这种奇点 称为稳定节点。 4)不稳定节点:相轨迹非周期地趋向于发散,这种奇点称为不稳 定节点, 5)鞍点:相轨迹是一族“双曲线”,属于不稳定平衡状态。 6)中心:奇点附近的相轨迹是一族封闭曲线,这种奇点称为中心

第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 价系砖奇点,的莞夏 2.2结物的定义 同哪:什么是变销物系统? 它不指艺制廉禁的物建的构,也不滑能框图形式的 变构制variable.structure control,,VC本上是 不定竹 结构。“结构"是一种龙性的晨意,它应能定性地反 映控的内在性质。 的性:其性表现为控制的不连 的不之在手的 长@ 拉制暴峡的许多定性性质海可在系峡的相轨迹中反映 ”并不电可以在中,菜当首 的状态如售楚及其各阶号量等有目的地不断变化,撞使 定点 出来,加系筑的定性、近特性、快道性、, 下定滑列 不晚室焦点 行性及系统行为的鲁排性等。所以,相轨迹槽峰丁 sliding mode control, 的内在特性。 SMG,厚滑模3完地物业制: 中6点 第二节变结构控制理论基础 第二节变结构控制理论基础 第三节变结构控制系统基本概念 党义1:系镜始物 性童: 3.1变结构系统的定义 燕旋的种物执为族的一种揽型,即由某想敬学力复 不是航有的变站构控圳常能滑满边圳。而滑满拉制是变结构 广义地说,在控制过程(瞬态过程)中,系统结构(模型 插述的模包。装有几种不门的时牌。薰通黄它有九神 拉制中最生毫的设计方凌。 可发生变化的系统。叫变结构系统 阻不同微学瘦达式表站的情道。 通俗花法, 1=x 党义2:滑种模体 如设有系统: 如果存在一个(成几个)切换■蒙遍系峡的快态达到问黄 人为慢定一曼过平物燕的指球连,题过量当设计,系城 X:=aX 西章值时,票峡从一个帕构自动转换成易一个南定的蜂构。 状基点沼着此相教旋渐近滑定到平青点。成港象地源为滑 那金达补射构藏之为变站构系候。 则此系统的特征方程为:p2-日,0 肉干餐点的一种运动,指动执达的”指功二字即未于 若保持不变,则不论取什么值,此系统都不会渐近稳定 7
7 第二节 变结构控制理论基础 第二节 变结构控制理论基础 2.2 结构的定义 它不指控制系统的物理结构,也不指系统框图形式的 结构。“结构”是一种定性的概念,它应能定性地反 映控制系统的内在性质。 控制系统的许多定性性质都可在系统的相轨迹中反映 出来,如系统的稳定性、渐近特性、跟踪快速性、振 荡特性及系统行为的鲁棒性等。所以,相轨迹描绘了 系统的内在特性。 第二节 变结构控制理论基础 问题:什么是变结构系统? 变结构控制(variable. structure control, VSC)本质上是 一类特殊的非线性控制,其非线性表现为控制的不连续 性。这种控制策略与其他控制的不同之处在于系统的 “结构”并不固定,可以在动态过程中,根据系统当前 的状态(如偏差及其各阶导数等)有目的地不断变化,迫使 系统按照预定“滑动模态”的状态轨迹运动,所以又常 称变结构控制为滑动模态控制(sliding mode control, SMC),即滑模变结构控制。 第二节 变结构控制理论基础 定义1:系统结构 系统的一种结构为系统的一种模型,即由某一组数学方程 描述的模型。系统有几种不同的结构,就是说它有几种 (组)不同数学表达式表达的模型。 定义2 :滑动模态 人为设定一经过平衡点的相轨迹,通过适当设计,系统 状态点沿着此相轨迹渐近稳定到平衡点,或形象地称为滑 向平衡点的一种运动,滑动模态的”滑动“二字即来源于 此。 第二节 变结构控制理论基础 注意: 不是所有的变结构控制都能滑模控制,而滑模控制是变结构 控制中最主流的设计方法。 通俗说法: 如果存在一个(或几个)切换函数,当系统的状态达到切换 函数值时,系统从一个结构自动转换成另一个确定的结构, 那么这种结构称之为变结构系统。 第三节 变结构控制系统基本概念 3.1变结构系统的定义 广义地说,在控制过程(瞬态过程)中,系统结构(模型) 可发生变化的系统,叫变结构系统。 如设有系统: 则此系统的特征方程为: 若a保持不变,则不论a取什么值,此系统都不会渐近稳定