2、主要结论 (1)原子大小和轨道半径 耳末 m.v2 e? 2,→my2= e nh Ln=m.ynyn=nh,-→yn= nh m.r m. m.r r 方2 2n2=a,n2 方2 r m a。= ≈0.529A 4π6,h2 me? (a。= me2 (国际单位制) ac e2 1 Vn= e21_ e h n (0= n hc137 4πEohc
2、 主要结论 (1) 原子大小和轨道半径 r e vm r e r vm e e 2 2 2 2 2 , =→= ne nnen n rm n vnrvmL = =, =→== ,)( 2 2 ne n e r e rm n m = = 2 0 2 2 2 nan em r e n == = A. em a e 5290 2 2 0 ≈= = ) 4 ( 2 2 0 0 em a e πε = = n c n e vn α =⋅= 1 2 = 137 1 2 ≈= c e = α ) 4 ( 0 2 c e πε = α = (国际单位制)

例题试计算氢原子的第一玻尔轨道的半径。 解答: 方2 (1.0545×10-2"erg·s)2 me2 9.11×10-8g×(4.803×10-"esu)2 =5.29×10-9cm (厘米克秒静电单位制) 4π×8.854×10-2×(1.0545×10-4J·s)2 ao 4πEh2 m.e2 9.11×10-31g×(1.602×10-9C)2 =5.29×10-"m (国际单位制)
cm g esu serg em a e 9 28 10 2 27 2 2 2 0 1029.5 )10803.4(1011.9 100545.1( ) − − − − ×= ××× × ⋅ == = 例题 试计算氢原子的第一玻尔轨道的半径。 解答: m kg C sJ em a e 11 31 219 12 34 2 2 2 0 0 1029.5 )10602.1(1011.9 4 )100545.1(10854.84 − − − − − ×= ××× × × × × ⋅ == πε = π (国际单位制) (厘米克秒静电单位制)

(2)定态能量 T= 1 V=- 2 2r 1e2 E=T+V=- 2 r 2 r= me n'=aon e2 1 1 E. m.e n2, n=1,2,. 2a。n2 2h2 E,≈-13.6eV (国际单位制) E,-136x(ew) (En= me 1 2(4E0)2方2n2
(2) 定态能量 " = ,n n em na e E e n 21, 1 2 1 2 224 2 0 2 −=−= = r e VTE r e V r e e vmT 2 2 2 2 2 1 , 2 1 2 1 −=+= −=== 2 0 2 2 2 nan em r e n == = ) 1 )4(2 ( 222 0 4 n em E e n πε = −= E1 ≈ − 6.13 eV VE 2 1 = )( 1 6.13 2 eV n En ×−≈ (国际单位制)

例题试计算氢原子的第一玻尔轨道能量。 解答: E,= me 9.11×10-2g×(4.803×10-0esu)4 2h2 2×(1.0545×10-2”erg·s)2 =2.179×10-"erg=13.6eV E,三 me 2(4π6)2h2 9.11×10-3kg×(1.602×10-9C)4 2×(4π×8.854×10-2)2×(1.0545×10-4J·s)2 =2.179×10-18J=13.6eV
例题 试计算氢原子的第一玻尔轨道能量。 解答: erg eV serg em g esu E e 10179.2 6.13 100545.1(2 ) )10803.4(1011.9 2 11 27 2 28 10 4 2 4 1 ×= = ⋅×× ××× −=−= − − − − = eVJ sJ kg C em E e 6.1310179.2 )100545.1()10854.84(2 )10602.1(1011.9 )4(2 18 212 34 2 31 419 22 0 4 1 =×= ⋅××××× ××× = −= − − − − − π πε =
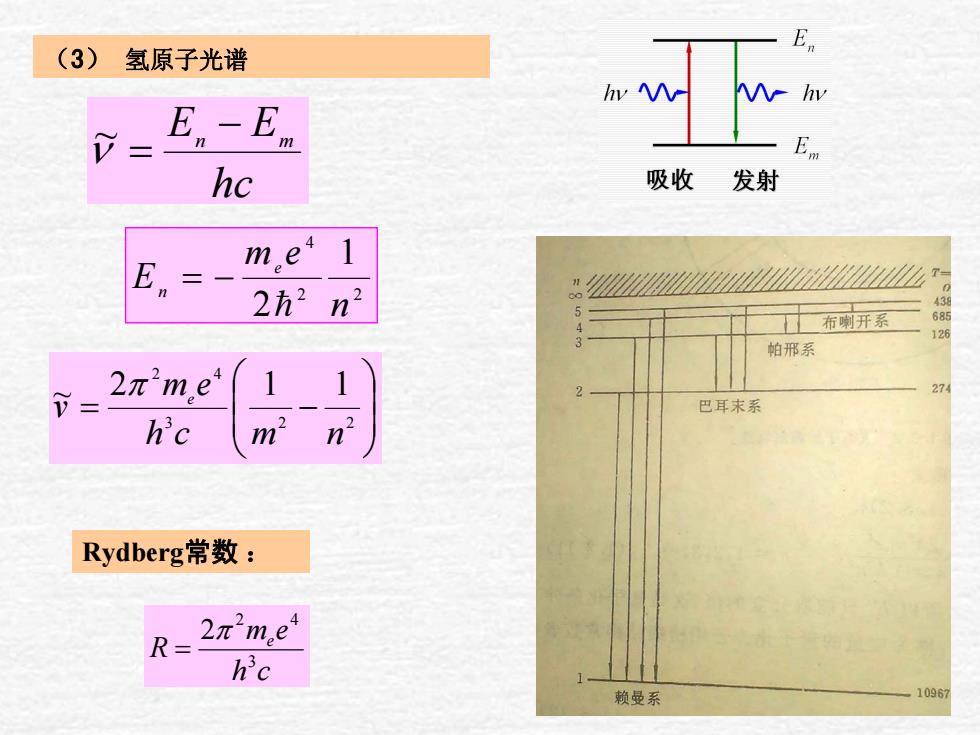
(3) 氢原子光谱 = E。-Em hc 吸收发射 me 2h2n2 布喇开系 126 帕邢系 2π2m,e 1 巴耳末系 hc Rydberg?常数: 2π2m.e hc 赖曼系 1096
(3) 氢原子光谱 hc − EE mn ν = ~ 22 4 1 2 n em E e n = −= ⎟⎟⎠⎞ ⎜⎜⎝⎛ = − 3 22 42 ~ 2 11 nmch em v π e ch em R e 3 42 2π = Rydberg常数 :