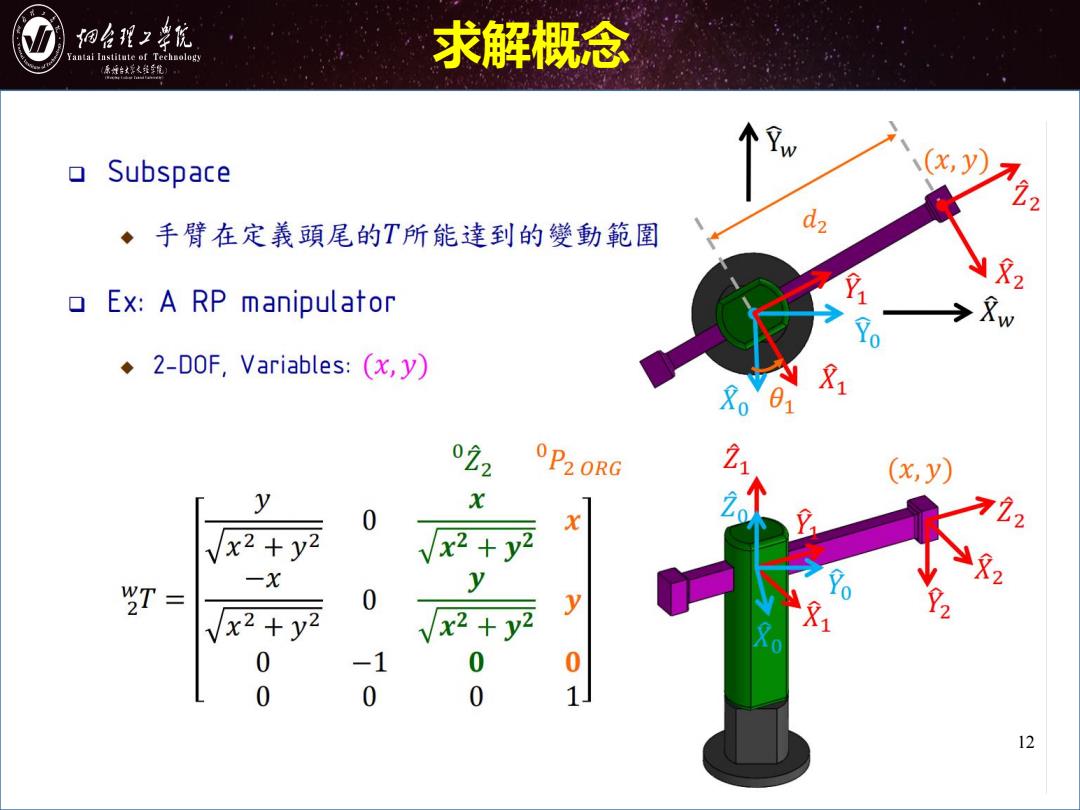
细台程2幸优 Yantai Institute of Technology 求解概念 原城台好火维年馆 Subspace ◆手臂在定義頭尾的T所能達到的變動範圍 2 Ex:A RP manipulator Xw 2-DOF,Variables:(x,y) 8001 81 0P2ORG (x,y) y X 0 X 22 x2+y2 √x2 y2 X2 WT= 0 Vx2+y2 vx2 y2 y 00 -1 0 0 0 0 1」 12
12 求解概念

细台程2幸优 antai Institute of Technology 多重解 原城台好火维年院 ▣解的數目 ◆由於是nonlinear transcendental equations,6未知數6方程式不代表具 有唯一解 13
13 多重解

阳台程2幸院 antai Institute of Technology 多重解 原城台好父维年航 口解的數目 ◆由於是nonlinear transcendental equations,6未知數6方程式不代表具 有唯一解 ◆是由joint數目和link參數所决定 Ex:A RRRRRR manipulator ai 解的數目 a1=a3=a5=0 ≤4 a3=a5=0 ≤8 a3=0 ≤16 Alla:≠0 ≤16 14
14 多重解

阳台程2幸优 antai Institute of Technology 多重解 原城台好火维年馆 Ex:PUMA (6 rotational joints) ◆針對特定工作點’8組解 ·前3軸具有4種姿態 如右圖所示 15
15 多重解

细台形2幸院 antai Institute of Technology 多重解 原城台好火维年馆 Ex:PUMA (6 rotational joints) ◆針對特定工作點,8組解 ·前3軸具有4種姿態 如右圖所示 ◆每一個姿態中,具有2組手腕轉動 姿態 04=04+180 05=-05 06=06+180° 16
16 多重解