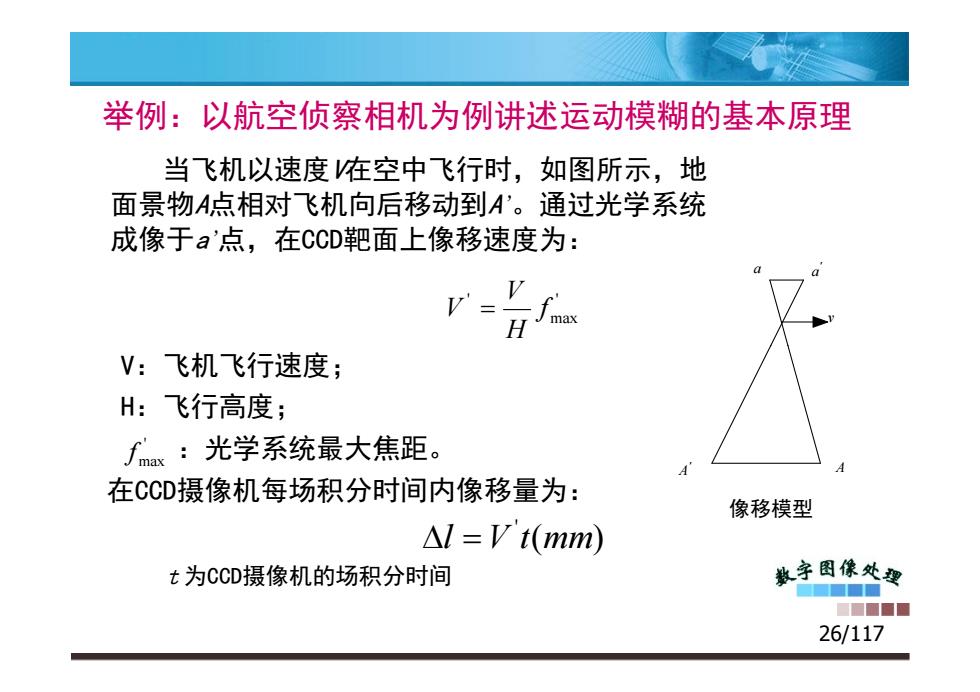
举例:以航空侦察相机为例讲述运动模糊的基本原理 当飞机以速度在空中飞行时,如图所示,地 面景物A点相对飞机向后移动到A'。通过光学系统 成像于a'点,在CCD靶面上像移速度为: H max V:飞机飞行速度; H:飞行高度; fx:光学系统最大焦距。 在CCD摄像机每场积分时间内像移量为: 像移模型 △l=Vt(mm) t为CCD摄像机的场积分时间 数字图像处要 ■■■■ ■■■■题 26/117
举例:以航空侦察相机为例讲述运动模糊的基本原理 当飞机以速度V在空中飞行时,如图所示,地 面景物A点相对飞机向后移动到A’。通过光学系统 成像于a’点,在CCD靶面上像移速度为: v a a ' ' max ' f H V V 26/117 V:飞机飞行速度; H:飞行高度; :光学系统最大焦距。 在CCD摄像机每场积分时间内像移量为: t为CCD摄像机的场积分时间 A ' A 像移模型 ' max f ( ) ' l V t mm

小结: 像移量的存在导致图像模糊,为得到清晰图像,必须要对 像移进行控制。在实际工程中,CCD的积分时间不能无限的缩 小,而且高帧频CCD的价格很贵。积分时间缩短后,为了保证 图像质量,所需的地面照度就越大,这就限制了相机的工作条 件,在许多情况下是不能接受的。 目前解决运动模糊的主要手段是通过了解图像的退化过程, 建立运动图像的复原模型,通过数学模型来解决图像的复原问 题。 数字图像处要 ■■■■ ■■■■■ 27/117
小结: 像移量的存在导致图像模糊,为得到清晰图像,必须要对 像移进行控制。在实际工程中,CCD的积分时间不能无限的缩 小,而且高帧频CCD的价格很贵。积分时间缩短后,为了保证 图像质量,所需的地面照度就越大,这就限制了相机的工作条 27/117 件,在许多情况下是不能接受的。 目前解决运动模糊的主要手段是通过了解图像的退化过程, 建立运动图像的复原模型,通过数学模型来解决图像的复原问 题

8.2.2运动模糊图像的退化模型 >模糊图像的一般退化模型: 在实际降质过程中,降质的另一个复杂因素是随机噪声, 考虑有噪声的图像恢复,必须知道噪声统计特性以及噪声和图 像信号的相关情况,这是非常复杂的。 实际中假设是白噪声--频谱密度为常数,且与图像不相 关,(一般只要噪声带宽比图像带宽大得多时,此假设成立), 由此得出图像退化模型。 可以将图像退化过程描述成一个退化系统,这里原图像f(x,) 是通过一个系统H并与加性噪声(x,y)相加退化成图像g(x,y) 的,其过程如下图所示: 数字图像处要 ■■■■ ■■■■■ 28/117
在实际降质过程中,降质的另一个复杂因素是随机噪声, 考虑有噪声的图像恢复,必须知道噪声统计特性以及噪声和图 像信号的相关情况,这是非常复杂的。 8.2.2 运动模糊图像的退化模型 模糊图像的一般退化模型: 28/117 实际中假设是白噪声---频谱密度为常数,且与图像不相 关,(一般只要噪声带宽比图像带宽大得多时,此假设成立), 由此得出图像退化模型。 可以将图像退化过程描述成一个退化系统,这里原图像 是通过一个系统 并与加性噪声 相加退化成图像 的,其过程如下图所示: f x y ( , ) H n x y ( , ) g x y ( , )
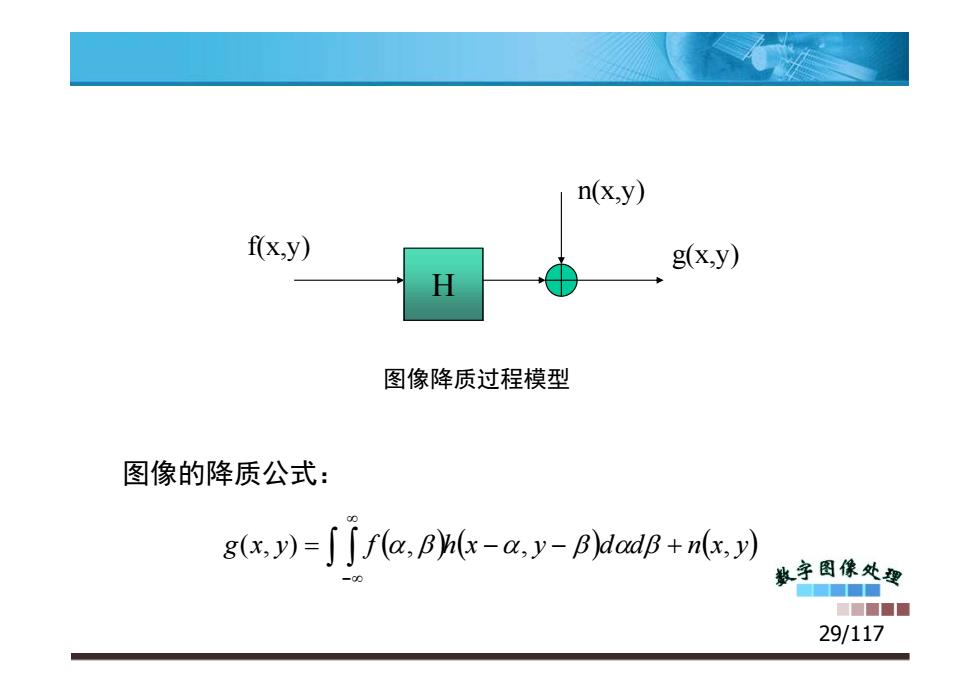
n(x,y) fxy) g(x,y) 图像降质过程模型 图像的降质公式: gx,y)=∫∫fa,Bhx-a,y-BdadB+nx,y) 数字图像处要 ■■■■ ■■■■■ 29/117
H f(x,y) g(x,y) n(x,y) 29/117 g(x, y) f , h x , y d d n x, y 图像降质过程模型 图像的降质公式:

首先对降质函数H作以下假设: ①H是线性的 H[k f (x,y)+kf (x,y)]=k Hf (x,y)+kHf (x,y) ②H是空间(或移位)不变的 对任一个f(x,y)和任一个常数B都有: H f(x-a,y-B)=8(x-a,y-B) 就是说图像上任一点的运算结果只取决于该点的输入值, 而与坐标位置无关。 数字图像处要 ■■■■ ■■■ 30/117
首先对降质函数H作以下假设: H是线性的 H是空间(或移位)不变的 对任一个 和任一个常数 都有: H k f x, y k f x, y k Hf x, y k Hf x, y 1 1 2 2 1 1 2 2 f x y , 、 30/117 对任一个 和任一个常数 都有: 就是说图像上任一点的运算结果只取决于该点的输入值, 而与坐标位置无关。 f x y , 、 H f x y g x y ( - , - ) ( - , - )