
第9章形态学图像处理 407 一幅子图像来处理,而不是一幅图形)。图9.7()显示了使用这个结构元对原图像进行膨胀后的结果。裂 缝已被桥接。形态学方法较之我们在图4.49中用于桥接断裂的低通滤波方法的一个直接的优点,就是形 态学方法可在一幅二值图像中直接得到结果。另一方面,低通滤波方法则从一幅二值图像开始,生成 幅灰度图像,它需要用一个园值函数将灰度图像转换为二值图像。 a b c Historically.certain computer rams were written ere written usin our to define the appticable rn.the than th 2000. ea 图9.7(a)具有断裂字符的低分辨率样品文本(见放大的视图): (b)结构元:(⊙)图)对a的张。断裂线段被连起来了 9.2.3对偶性 膨胀和腐蚀彼此关于集合求补运算和反射运算是对偶的,即 (A9B)=A⊕B (9.25) 和 (A⊕B=AOB (92-60 式(9.25)指出.B对A的腐蚀是B对A的膨胀的补,反之亦然。当结构元关于其原点对称时(G通常 如此),因为B=B,故对偶性特别有用。这样,我们可以用相同的结构元简单地使用B膨胀图像的 背景(即膨胀A),并对该结果求补就可得到B对该幅图像的腐蚀。类似的说明适用于式(9.2-6)。 为了说明建立形态学表达式有效性的一种典型方法,我们正式证明式(925)的有效性。由腐蚀 的定义,我们有 (AOB)=(B).CA 如果集合(B),包含在集合A中,则(B),∩A=⑦,在这种情况下,上式变为 (AOB)=(B)nA=0 但是,满足(B).∩A=⑦的z的集合的补集是满足(B),∩A°≠⑦的z的集合,因此。 (AeB)={zI(B),nA≠O=A⊕B 其中,最后一步来自式(9.23)。这就结束了该证明。采用类似的推理可以证明式(9.2-6)(见习题9.13) 9.3开操作与闭操作 如您所见到的那样,膨胀会扩大一幅图像的组成部分,而腐蚀则会缩小一幅图像中的组成部分 在本节中,我们讨论另外两个重要的形态学操作:开操作与闭操作。开操作一般会平滑物体的轮廓、 断开较窄的狭颈并消除细的突出物。闭操作同样也会平滑轮廓的一部分,但与开操作相反,它通常会 弥合较窄的间断和细长的沟壑,消除小的孔洞,填补轮廓线中的断裂。 6

408 数字图像处理(第三版) 结构元B对集合A的开操作,表示为A。B,其定义如下: AB=(AOB)©B (9.3.1) 因此,B对A的开操作就是B对A的腐蚀,紧接着用B对结果进行膨张」 类似地,用结构元B对集合A的闭操作,表示为AB,定义如下: AB=(A⊕B)B (9.3-2 上式说明,B对集合A的闭操作就是简单地用B对A膨胀,紧接着用B对结果进行腐蚀 开操作有一个简单的几何解释(见图9.8)。假设我们把结构元B视为一个(扁平的“转球”。然 后,A。B的边界由B中的点建立:当B在A的边界内侧滚动时,B所能到达的A的边界的最远点。 开操作的这种几何拟合特性导致了一个集合论公式,该公式表明B对A的开操作是通过拟合到A的 B的所有平移的并集得到的。也就是说,开操作可以表示为一个拟合处理: AB=UH(B),I(B),∈A} (9.3-3 其中U表示大括号中所有集合的并集 A●B=U(B周(B,CA a b e d 在中的平移 ·)8 图9.8(a结构元B沿集合A的内侧边界滚动(黑点表示B的原点);(6)结构元:(©)粗线是开操 作的外部边界(完全的开操作(阴影部分)。为清楚起见,在图(中我们未对A加阴影 除了我们现在是在边界的外侧滚动B(见图9.9)之外,闭操作有类似的几何解释。如下面所讨论 的那样,开操作和闭操作彼此对偶,所以闭操作在边界外侧滚动球体是意料之中的事情。从几何上讲, 当且仅当对包含w的(B),进行的任何平移都有(B),∩A≠O时,点w才是AB的一个元素。图9.9说 明了闭操作这一基本的几何性质 a b c 图9.9()结构元B沿集合A的外侧边界滚动:(⑥)粗线是闭操作的外部边界 (C完全的闭操作(阴影部分)。为清楚起见.在图(a中我们末对A加阴影 例9.3形态学开操作和闭操作的简单说明 55网 图9.10进 步说明了开操作和闭操作。图9,.10(@显示了一个集合A,图9.106)显示了腐蚀处理期 65网间一个圆盘形结构元的各个位置。当腐蚀完成后,得到图9.10()所示的分离的图形。注意.两个主要部

第9章形态学图像处理 409 分之间的桥接的消失。桥接部分的宽度与结构元的直径相比要细:也就是说,集合的这部分不能完全包 含结构元,因此违反了式(⑨.21)的条件。该物体最右边的两个部分也是如此。圆盘无法拟合的突出部分 已被消除。图9.10()显示了对腐蚀后的集合进行膨胀的处理,图9.10(©)显示了开操作的最终结果。注 意,方向向外的角变圆了,而方向向内的角则未受影响。 类地。图9.10(0到()显示了使用同一结构元对A进行闭操作的结果。我们注意到方向向内的角 圆了,而方向向外的角则保持不变。在A的边界上,最左边的突人部分的尺寸明显地减小了,因为在这 个位置上圆盘无法拟合。还要注意使用圆盘形结构元对集合A进行开操作和闭操作所得到的物体的各个 部分都平滑了。 A马 A·B=A⊙B)⊕B A·B=ABB)©B 图9.10形态学开操作和闭操作。结构元是在图(6)中的各个位置显 示的小圆。为清楚起见,SE未加阴影。黑点是结构元的中心 如同膨张和腐蚀的情形那样,开操作和闭操作彼此关于集合求补和反射也是对偶的。即 (AB)=(A。B (9.3-4) (A。B°=(A.B) 93.5) 我们将该结果的证明作为练习留给读者(见习题9.14)。 开操作满足下列性质: (aA。B是A的一个子集(子图像)。 ()如果C是D的一个子集,则C。B是DB的一个子集 (C)(AB)。B=AB

410 数宇图像处理(第三版) 类似地,闭操作满足下列性质: (a)A是AB的一个子集(子图像) (b)如果C是D的一个子集,则CB是DB的-个子集。 (C(A-BB=A-B。 注意,由两种情况下的条件()可知,算子应用一次后,一个集合的多次开操作或闭操作没有影响 例9.4针对形态学滤波使用开操作和闭操作。 形态学操作可用于构造与第3章中讨论的空间滤波概念相类似的滤波器。图9.11(a中的二值图像显 示了被噪声污染的指纹图像的一部分。这里,噪声本身表现为在黑色背景上的随机亮元素和指纹较亮部 分上的暗元素。我们的目的是消除噪声及其对印刷的影响,同时使图像的失真尽可能小。由开操作后紧 跟着闭操作组成的形态学滤波器可用来实现这一目的。 e f AeB=A· A·B)⊙B台B=(A·B)·B 图9.11(a噪声图像;b)结构元:(c)腐蚀后的图像:(@A的开操作:(e)开操作 的膨胀:(们开操作的闭操作(原图由美国国家标准和技术研究所提供 图9.11(6)显示了所用的结构元。图9.11的余下部分显示了滤波操作一步步的顺序。图9.11()显示 了使用结构元对A进行腐蚀的结果。背景噪声在开操作的病蚀阶段被完全消除,因为这种情况下的所有 噪声分量都比结构元小。包含在指纹中的噪声元素(黑点)的尺寸实际上却增大了。原因是当物体被腐蚀 时,这些元素在尺寸增大的内部边界。这种增大可通过对图9.11()执行影胀来抵消。图911()显示了该 结果,指纹中包含的噪声分量的尺寸被减小了,或完全被消除了 刚才描述的两个操作构成了B对A的开操作。我们注意到,在图9.11()中,开操作的实际效果实质 网上是从背景和指纹本身中消除所有的噪声。然而,在指纹纹路间却产生了新的断裂。为防止这种不希望 6的影响,我们在开操作上执行膨胀,如图9,1()所示。大部分断裂被恢复了,但纹路却变粗了,这是可
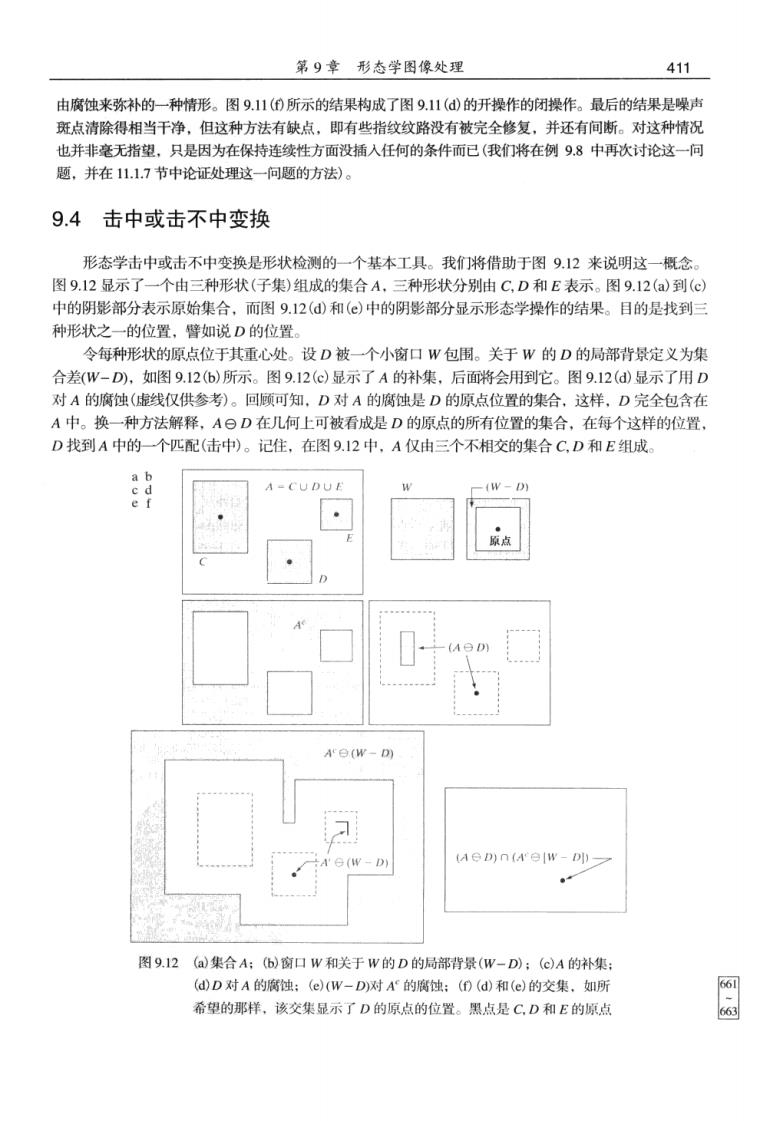
第9章形态学图像处理 411 由腐蚀来弥补的一种情形。图9.11()所示的结果构成了图9.11()的开操作的闭操作。最后的结果是噪士 斑点清除得相当干净。但汶种方法有缺点。即有些指纹纹路没有被完全修复,并还有问断。对这种情况 也并非毫无指望,只是因为在保持连续性方面没插入任何的条件而已(我们将在例9,8中再次讨论这一问 题,并在11.1.7节中论证处理这一问题的方法)。 9.4击中或击不中变换 形态学击中或击不中变换是形状检测的一个基本工具。我们将借助于图9.12来说明这一概念 图9.12显示了一个由三种形状(子集)组成的集合A,三种形状分别由C,D和E表示。图9.12(a)到() 中的阴影部分表示原始集合,而图9.12(d)和()中的阴影乡部分显示形态学操作的结果。目的是找到三 种形状之一的位置,譬如说D的位置 令每种形状的原点位于其重心处。设D被一个小窗口W包围。关于W的D的局部背景定义为集 合差(W-D),如图9.12(6)所示。图9.12(⊙)显示了A的补集,后面将会用到它。图9.12(@)显示了用D 对A的腐蚀(虚线仅供参考)。回顾可知,D对A的腐蚀是D的原点位置的集合,这样,D完全包含在 A中。换一种方法解释,A©D在几何上可被看成是D的原点的所有位置的集合,在每个这样的位置 D找到A中的一个匹配(击中)。记住,在图9.12中,A仅由三个不相交的集合C,D和E组成。 A-CUDUE -(W-D 原点 A⊙D)n(A'白W-D小1 图9.12(a集合A:)窗口W和关于w的D的局部背景(W-D):(C)A的补集: (dD对A的腐蚀:(e)(W-D)对A的腐蚀:(D(d)和(e)的交集,如所 6网 希望的那样,该交集显示了D的原点的位置。黑点是C,D和E的原店