
解:薛定谔方程须注意的几个问题 (1)w是薛定谔方程的解,它是空间坐标x,y,z的 函数,解薛定谔时,为了方便起见,要把直角坐标表示的妙 (x,y,z)改换成球极坐标表示的y(y,O,9),二者关 系如下:
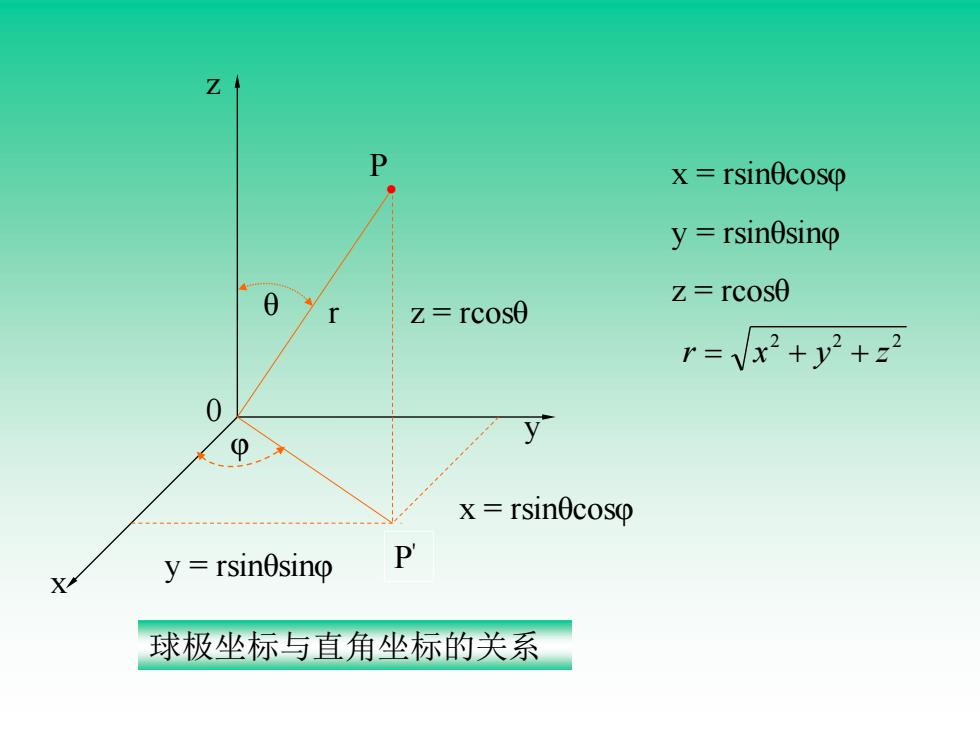
解:薛定谔方程须注意的几个问题 (1) ψ是薛定谔方程的解,它是空间坐标x,y,z的 函数,解薛定谔时,为了方便起见,要把直角坐标表示的ψ (x,y,z)改换成球极坐标表示的ψ(γ,θ, φ),二者关 系如下:
Z P x rsinecoso y rsinesino 0 z=rcos0 r z=rcos0 r=x2+y2+z2 0 x rsinecoso y rsinOsino P 球极坐标与直角坐标的关系
• P P ' 0 z y x θ φ z = rcosθ y = rsinθsinφ x = rsinθcosφ r x = rsinθcosφ y = rsinθsinφ z = rcosθ 2 2 2 r = x + y + z 球极坐标与直角坐标的关系

(2)薛定谔方程的解为系列解,每个解都要受三 个常数n,1,m的规定,这几个常数成为量子数 (3)每个解的球坐标可表示成两部分函数的乘积 w(r,0,0)=R(r)Y(0,0)
(2)薛定谔方程的解为系列解,每个解都要受三 个常数 n,l,m 的规定,这几个常数成为量子数 (3)每个解的球坐标可表示成两部分函数的乘积 ψ(r,θ,φ)= R(r)·Y( θ,φ)

(二)原子轨道和波函数 为了方便起见,量子力学借用Bohr 理论中“原子轨道的概念,将波函数仍 称为原子轨道,但二者的涵义截然不同
(二)原子轨道和波函数 为了方便起见,量子力学借用Bohr 理论中“原子轨道的概念,将波函数仍 称为原子轨道,但二者的涵义截然不同

波函数的每个解对应一个运动状态, 即一个原子轨道。因为每个解受到三个 常数的规定,因此一个波函数(一个运 动状态或一个原子轨道)可以简化为用 一组量子数(n,/,m)来表示
波函数的每个解对应一个运动状态, 即一个原子轨道。因为每个解受到三个 常数的规定,因此一个波函数(一个运 动状态或一个原子轨道)可以简化为用 一组量子数(n,l,m)来表示