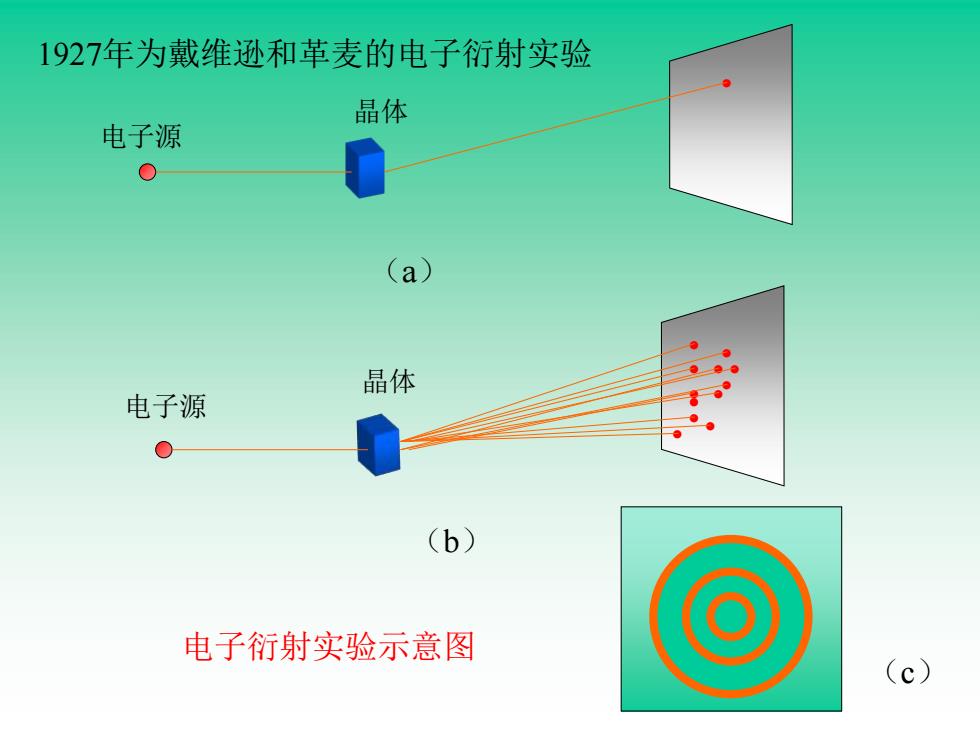
1927年为戴维逊和革麦的电子衍射实验 晶体 电子源 0 (a) 晶体 电子源 0 (b) 电子衍射实验示意图 (c)
• 电子源 晶体 (a) • • • • • • • • • • • • 电子源 晶体 (b) (c) 电子衍射实验示意图 1927年为戴维逊和革麦的电子衍射实验

从电子衍射图象可以看出:衍射强度(即电子波强 度)大的地方,电子出规的机会多,或用数学术语讲, 电子出现的概率大;衍射强度小的地方,电子出现的橇 率小。 也就是说,空间任何一点波的强度和微粒(电子)在 该处出现的概率呈正比,所以,物质波是大量粒子在统计 行为下的几率波(probability waves)
从电子衍射图象可以看出:衍射强度(即电子波强 度)大的地方,电子出现的机会多,或用数学术语讲, 电子出现的概率大;衍射强度小的地方,电子出现的概 率小。 也就是说,空间任何一点波的强度和微粒(电子)在 该处出现的概率呈正比,所以,物质波是大量粒子在统计 行为下的几率波(probability waves)

3、氵 测不准原理 对于具有波粒二象性的微粒如电子等来说,它的运动状 态不能用经典力学来描述。 无法同时准确的测定它在某一瞬间的位置和速度(或动 量),如果微粒的运动位置测得越准确,则相应的速度测的越 不准确,反过来,它的速度测的越准确,相应的运动位置测得 越不准确。这就是1927年,HeisenbergW(海森堡)提出来的 著名的测不准原理(uncertainty principle) h △x·△y≥ 72 测不准原理并不是说微观离子的运动就无规律可言,只 是说它不符合经典力学的魏律,我们应孩用量子力学来描述 微观粒子的运动
3、测不准原理 对于具有波粒二象性的微粒如电子等来说,它的运动状 态不能用经典力学来描述。 测不准原理并不是说微观离子的运动就无规律可言,只 是说它不符合经典力学的规律,我们应该用量子力学来描述 微观粒子的运动。 无法同时准确的测定它在某一瞬间的位置和速度(或动 量),如果微粒的运动位置测得越准确,则相应的速度测的越 不准确,反过来,它的速度测的越准确,相应的运动位置测得 越不准确。这就是1927年,HeisenbergW(海森堡)提出来的 著名的测不准原理(uncertainty principle) m h x v

三、 氢原子的量子力学模型 (一)、薛定谔方程一电子运动的波动方程式 a2w.a2wa2yw.8π2m 022 3 E-)w=0 式中:m是电子的质量;x,y,z是电子的空间坐标; E是电子的总能量; V是电子的势能; h为普朗克常数。 功称为波函数(wave function),是空间坐标x,y,z 的函数
二、氢原子的量子力学模型 (一)、薛定谔方程—电子运动的波动方程式 ( ) 0 8 2 2 2 2 2 2 2 2 + − = + + E V h m x y z 式中:m 是电子的质量; x,y,z 是电子的空间坐标; E 是电子的总能量; V 是电子的势能; h 为普朗克常数。 ψ 称为波函数(wave function),是空间坐标 x,y,z 的函数

量子力学用波函数Ψx,y,2ノ和其相应的能量E来描述 电子的运动状态。波函数本身的物理意义不明确,但波函数 绝对值的平方却有明确的物理意义,即: WP表示在空间某处电子出现的概率密度(probability density),也就是在该点周围微单位体积中电子出现的概率
量子力学用波函数ψ(x,y,z)和其相应的能量E来描述 电子的运动状态。波函数本身的物理意义不明确,但波函数 绝对值的平方却有明确的物理意义,即: |ψ|2表示在空间某处电子出现的概率密度(probability density),也就是在该点周围微单位体积中电子出现的概率